【机器学习】5.支持向量机

间隔与支持向量

给定数据集D={$(x_1,y_1),(x_2,y_2),...,(x_m,y_m)$},$y_i\in [-1,+1]$训练的基本思想就是基于训练集D在样本空间找到一个划分超平面。
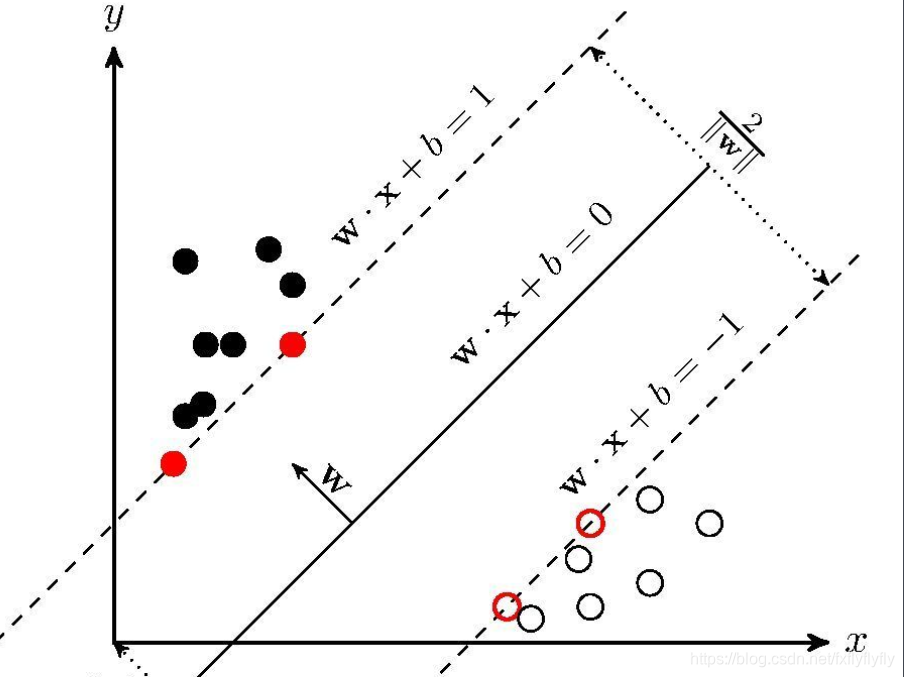在样本空间中，划分超平面可通过如下线性方程来描述
$$W^{T}x+b=0$$
其中$w=(w_1,w_2,...,w_d)$为法向量，决定超平面的方向，b为位移量，决定超平面与原点治安的距离，记为（w，b）
样本空间中任意点x到超平面（w，b）的距离为：
$$r=\frac{|W^{T}x+b|}{||w||}$$
若将w，b等比例增大，例如2w，2b，超平面未改变，但函数间隔缺改变了，所以除以||w||。

若超平面划分正确，则有:
$$\{\begin{array}{ll}{w}^T{x}_i+b>0,& y_i=+1\\ w^T{x}_i+b<0,& y_i=-1\end{array}$$
令：
$$\{\begin{array}{ll}{w}^T{x}_i+b\ge 1,& y_i=+1\\ w^T{x}_i+b\le -1,& y_i=-1\end{array}$$
若训练样本使$w^T{x}_i+b=\pm 1$,则被称为支持向量，两个异类支持向量到超平面的距离之和成为间隔。
$$r=\frac{2}{||w||}$$
欲找到最大化间隔的划分超平面，即使r最大
$$ma{x}_{w,b}{\frac{2}{||w||}}_{s.t.y_i(w_T{x}_i+b\ge 1)}$$

即：
$$mi{n}_{w,b}0.5||w|{|}_{s.t.y_i(w_T{x}_i+b\ge 1)}^2$$

对偶问题

根据$mi{n}_{w,b}0.5||w|{|}_{s.t.y_i(w_T{x}_i+b\ge 1)}^2$
　　$f(x)=w^{T}x+b$ 　　　　　　求解得到最大间隔划分超平面
使用拉格朗日乘子法
$$L(w,b,\alpha )=\frac{1}{2}||w|{|}^2+\sum _{i=1}^m{\alpha }_i(1-y_i(w^T+b))$$
如此，问题就变成了:
$$ma{x}_{\alpha }mi{n}_{w,b}L(w,b,\alpha )$$

对L(w,b,α)的w，b求偏导并等于0.
$$\frac{\sigma L}{\sigma w}=w-\sum _{i=1}^m{\alpha }_i{y}_i{x}_i=0$$

$$\frac{\sigma L}{\sigma b}=\sum _{i=1}^m{\alpha }_i{g}_i=0$$

代入原式中
$$L(w,b,\alpha )=\frac{1}{2}(\sum _{i=1}^m{\alpha }_i{y}_i{x}_i{)}^2-\sum _{i=1}^m{\alpha }_i(1-y_i(\sum _{i=1}^m{\alpha }_i{y}_i{x}_i\ast x+b))=\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i{x}_j$$

即
$$ma{x}_{\alpha }L(w,b,\alpha {)}_{s.t.\{\begin{array}{l}{\sum }_{i=1}^m{\alpha }_i{y}_i=0\\ \alpha \ge 0\end{array}}$$

$${ma{x}_{\alpha }\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i{x}_j}_{s.t.\{\begin{array}{l}\alpha \ge 0\\ {\sum }_{i=1}^m{\alpha }_i{y}_i=0\end{array}}$$

求解
$$f(x)=w^{T}x+b=\sum _{i=1}^m{\alpha }_i{y}_i{x}_i^T{x}_i+b$$

核函数

在原始样本空间内也许不存在一个能正确划分两类样本的超平面，这是，我们可以将样本从原始空间映射到一个更高维的特征空间。
令$\Phi (x)$表示将x映射后的特征向量，则超平面为：
$$f(x)=w^T\Phi (x)+b$$
对应有
$${ma{x}_{\alpha }\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j（\Phi (x_i)\ast \Phi (x_j)）}_{s.t.\{\begin{array}{l}\alpha \ge 0\\ {\sum }_{i=1}^m{\alpha }_i{y}_i=0\end{array}}$$
因为 $\Phi (x_i)\ast \Phi (x_j)$难以计算，所以设想一个函数k
$$K(x_i,x_j)=<\Phi (x_i),\Phi (x_j)>=\Phi (x_i)\ast \Phi (x_j)$$
我们称K<·,·>为核函数
令x为输入空间，K<·,·>是定义在xxx上的对称函数，当且仅当对于任意数据$D=[X_1,X_2,..,x_m]$,核矩阵k总是半正定的，k使核函数。

$$K=\left[\begin{array}{ccccc}k(x_1,x_1)& ...& k(x_1,x_j)& ...& k(x_1,x_m)\\ ..& ...& ..& ...& ..\\ k(x_i,x_1)& ...& k(x_i,x_j)& ...& k(x_i,x_m)\\ ..& ...& ..& ...& ..\\ k(x_m,x_1)& ...& k(x_m,x_j)& ...& k(x_m,x_m)\end{array}\right]$$
常用核函数
$$k(x_i,y_i)=x_i{y}_i$$

$$k(x_i,y_i)=(x_i{y}_i{)}^d$$

$$k(x_i,y_i)=exp(-\frac{||x_i-x_j|{|}^2}{2{\sigma }^2})$$

$$........$$

软间隔和正则化

软间隔是允许某些样本不满足条件
$$y_i(w^T{x}_i+b)\ge 1$$
于是优化目标可以写成
$$mi{n}_{w,b}\frac{1}{2}||w|{|}^2+c\sum _{i=1}^m{\tau }_{0/1}(y_i(w^T{x}_i+b)-1)$$
其中C是大于0的常熟，${\tau }_{0/1}$是0/1的损失函数
$$\{\begin{array}{llc}1,& & \text{if z<0}\\ 0,& & \text{otherwise}\end{array}$$
当C为无穷大时，则等价为硬间隔，${\tau }_{0/1}$的数学性质不好，所以使用代替函数，常见有：
hinge损失：${\iota }_{hinge}(z)=max(0,1-z)$
指数损失：${\iota }_{exp}(z)=exp(-z)$
对率损失：${\iota }_{log}(z)=log(1+exp(-z))$
使用hinge损失，可将原始改为：
$$mi{n}_{w,b}\frac{1}{2}||w|{|}^2+c\sum _{i=1}^{m}max(0,1-y_i(w^T{x}_i+b))$$

引入松弛变量${\xi }_i\ge 0$
$$mi{n}_{w,b,\xi }1/2||w|{|}^2+c\sum _{i=1}^m{\xi }_i$$

$$s.t.y_i(w^T{x}_i+b)\ge 1-{\xi }_i$$

$${\xi }_i\ge 0$$

拉格朗日乘子法
$$L(w,b,\alpha ,\xi ,\mu )=1/2||w|{|}^2+c\sum _{i=1}^m{\xi }_i+\sum _{i=1}^m{\alpha }_i(1-{\xi }_i-y_i(w^T{x}_i+b))-\sum _{i=1}^m{\mu }_i{\xi }_i$$
对$w,b,\xi$求偏导。
$$w=\sum _{i=1}^m{\alpha }_i{y}_i{x}_i$$

$$0=\sum _{i=1}^m{\alpha }_i{y}_i$$

$$c={\alpha }_i+{\mu }_i$$

代入：
$$ma{x}_{{\alpha }_i}\sum _{i=1}^m{\alpha }_i-1/2\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_i{x}_i{x}_j$$

$$s.t.\sum _{i=1}^m{\alpha }_i{y}_i=0$$

$$0\le {\alpha }_i\le c$$

支持向量机回归

支持向量机回归能容忍$f(x)与y$之间有$\xi$的偏差，这就相当于以$f(x)$为中心，构建了一个宽度为$2\xi$的间隔带，只有训练样本落入间隔带，则认为是正确预测。
$$mi{n}_{w,b}1/2||w|{|}^2+c\sum _{i=1}^m{\zeta }_e(f(x_i)-y_i)$$
其中c为正则化常数，
$${\zeta }_e(z)=\{\begin{array}{ll}0,& if|z|\le ϵ\\ |z|-ϵ,& otherwise\end{array}$$
引入松弛变量，可改写为:
$$mi{n}_{w,b,{\xi }_i,{\hat{\xi }}_i}1/2||w|{|}^2+c\sum _{i=1}^m({\xi }_i+{\hat{\xi }}_i)$$

$$s.t.f(x_i)-y_i\le {ϵ}_i+{\xi }_i$$

$$y_i-f(x_i)\le {ϵ}_i+{\hat{\xi }}_i$$

$${\xi }_i\ge 0,{\hat{\xi }}_i\ge 0$$
引入拉格朗日乘子
$$L(w,b,\alpha ,\hat{\alpha },\xi ,\hat{\xi },\mu ,\hat{\mu })=1/2||w|{|}^2+c\sum _{i=1}^m(\xi +\hat{\xi })-\sum _{i=1}^m{\mu }_i{\xi }_i-\sum _{i=1}^m{\hat{\mu }}_i{\hat{\xi }}_i+\sum _{i=1}^m{\alpha }_i(f(x_i)-y_i-ϵ-{ϵ}_i)+\sum _{i=1}^m{\hat{\alpha }}_i(y_i-f(s_i)-ϵ-{\hat{\xi }}_i)$$

对$w,b,{\xi }_i,{\hat{\xi }}_i$求偏导为零
$$w=\sum _{i=1}^m({\hat{\alpha }}_i-{\alpha }_i)x_i$$

$$0=\sum _{i=1}^m({\hat{\alpha }}_i-{\alpha }_i)$$

$$c={\alpha }_i+{\mu }_i={\hat{\alpha }}_i+{\hat{\mu }}_i$$

代入上述$L(w,b,\alpha ,\hat{\alpha },\xi ,\hat{\xi },\mu ,\hat{\mu })$中：

$$ma{x}_{\alpha ,\hat{\alpha }}\sum _{i=1}^m({\hat{\alpha }}_i-{\alpha }_i)-ϵ({\hat{\alpha }}_i+{\alpha }_i)-1/2\sum _{i=1}^m\sum _{j=1}^m({\hat{\alpha }}_i-\alpha )({\hat{\alpha }}_j-\alpha )x_i{x}_j$$

$$s.t.\sum _{i=1}^m({\hat{\alpha }}_i-{\alpha }_i)=0$$

$$0\le ({\alpha }_i,{\hat{\alpha }}_i)\le c$$

核方法

定理：令H为核函数k对用的再生和希尔伯特空间，||h||_H表示H空间中关于h的范数，对于任意单调递增函数 $\Omega :[0,\infty ]\to R$和任意非负损失函数$\vartheta :R^m\to [0,\infty ]$，优化问题
$$mi{n}_{h\in H}F(h)=\Omega (||h|{|}_H)+\vartheta (h(x_1),h(x_2),...,h(x_m))$$

的解总可以写为：

$$h^{\ast }(x)=\sum _{i=1}^m{\alpha }_{i}k(x,x_i)$$