【机器学习】4.神经网络

神经网络是由具有适应性的简单单元组成的广泛互联并行的网络，它的组织能模拟生物神经系统对真是世界物体所做出的交互反应。

神经元模型

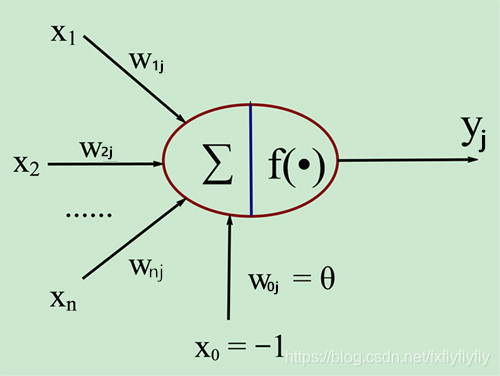神经元模型接收n个来自其他神经元传递的输出信号，这些输入信号通过带权重的连接进行传递，神经元接受的总输入值将于神经元的阈值进行比较，然后通过激活函数处理，产生神经元的输出。
理想激活函数
$$sgn(x)=\{\begin{array}{ll}1,& \text{if x>=0}\\ 0,& \text{if z<0}\end{array}$$
由于该阶跃函数不连续，不平滑所以使用
$$sigmoid(x)=\frac{1}{1+e^{-x}}$$

感知机与多层网络

感知机有两层神经元组成，能非常容易的实现逻辑与，非，或的运算。

学习规则：对训练样本（x，y）若当前感知机的输出为y^’，则
$$w_i=w_i+\Delta w$$
$$\Delta w=\eta (y-y^{{}^{\prime }})x_i\text{其中η属于(0,1)称为学习率}$$

单层感知机不能解决非线性可分问题
所以，多层网络被应用于此
我们将神经元不存在同层链接，也不存在跨层链接的神经网络结构称为‘多层前馈神经网络’

误差逆传播算法（BP神经网络）

通常所说的‘BP神经网络’是以BP算法训练的多层前馈神经网络。

给定训练姐D={（x₁,y₁），（x₂,y₂），…，（x_m,y_m）},x_i $\in$R^d,y_i&$\in$R^l,即输入示例有d个属性描述，输出l维实值向量。
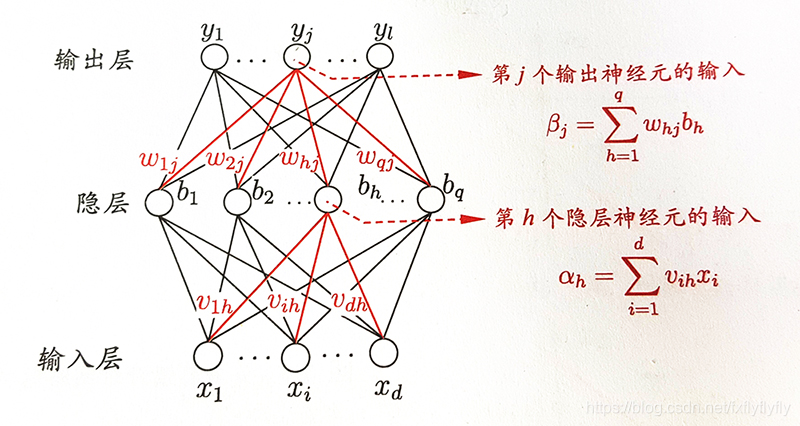再上图中:
隐层第h个神经元接受输入为：
$${\alpha }_h=\sum _{i=1}^d{v}_{ih}\ast x_i$$
输出层第j个神经元的接受输入为：
$${\beta }_j=\sum _{i=1}^q{w}_{hj}\ast b_h$$
对于训练例（x_k,y_k）,假定神经网络的输出为${\hat{y}}_k=({\hat{y}}_1^k,{\hat{y}}_2^k,...,{\hat{y}}_l^k)$即：
$${\hat{y}}_j^k=f({\beta }_j-{\theta }_j)$$
则，神经网络在训练例（x_k,y_k）上的均方误差为：
$$E_k=\frac{1}{2}\sum _{j=1}^l({\hat{y}}_j^k-y_j^k{)}^2$$
在BP神经网络中有 dq+ql+q+l 个参数需要确认，BP是一个迭代学习算法，任意参数v的更新估计式为：
$$v\leftarrow v+\Delta v$$
BP神经网络是基于梯度下降策略，以权值W_hj为例，给定学习率$\eta$
$$\Delta w_{hj}=-\eta \frac{\sigma E_k}{\sigma w_{hj}}$$
w_hj是先影响第j个输出层的输入值$\beta$_j,在影响其输出值$\hat{y}$_i^k,在影响E_K,所以：
$$\frac{\sigma E_k}{\sigma w_{hj}}=\frac{\sigma E_k}{\sigma {\hat{y}}_j^k}\ast \frac{\sigma {\hat{y}}_j^k}{\sigma {\beta }_j}\ast \frac{\sigma {\beta }_j}{\sigma w_{hj}}$$

由 $\beta$_j的定义

$$\frac{\sigma E_k}{\sigma w_{hj}}=b(h)$$

令
$$g_i=-\frac{\sigma E_k}{\sigma {\hat{y}}_j^k}\ast \frac{\sigma {\hat{y}}_j^k}{\sigma {\beta }_j}=-({\hat{y}}_j^k-y_j^k)f^{{}^{\prime }}({\beta }_j-{\vartheta }_j)={\hat{y}}_j^k(1-{\hat{y}}_j^k)(y_j^k-{\hat{y}}_j^k)$$

sigmoid函数：
$$f^{{}^{\prime }}(x)=f(x)(1-f(x))$$

所以：
$$\Delta {\vartheta }_{ij}=\eta g_j{b}_h$$
同理：
$$\Delta w_{ij}=-\eta g_j$$
$$\Delta v_{ij}=\eta e_n{x}_i$$
$$\Delta rh=-\eta e_n$$
其中：
$$e_n=-\frac{\sigma E_k}{\sigma b_n}\ast \frac{\sigma b_h}{\sigma a_n}=b_n(1-b_n)\sum _{j=1}^l{w}_{hj}{g}_j$$

BP神经网络经常遭遇过拟合问题，一般用两种方式防止
（1）早停（early stopping）：当训练误差减少但经验误差升高时，停止训练，且返回具有最小经验误差的连接值；
（2）正则化（regularization）：在误差目标函数上增加一个用于描述网络复杂度的部分，例如连接权和阈值的平方和。
$$E=\lambda \frac{1}{m}\sum _{k=1}^m{E}_k+(1-\lambda )\sum _i{w}_i^2$$
其中 $\lambda \in (0,1)$通常使用交叉验证发估计

局部最小与局部极小

局部最小不一定时全局最小，寻找全局最小的方法即跳出局部最小

• 以多组不同参数值初始化多个神经网络；
• 模拟退火，每一步以一定的概率接受比当前解更差的结果；
• 使用随机梯度下降（SGD），计算过程中加入了随机因素。

其他常见神经网络

（1）RBF网络：通常是一种单隐层前馈神经网络。可表示为：
$$\phi (x)=\sum _{i=1}^q{w}_i\rho (s,C_i)$$
$$\rho (x,C_i)=e^{-{\beta }_i||x-C_i|{|}^2}$$
其中q为隐层神经元的个数，C_I,W_I为隐层所对应的中心的权重
训练过程分两步：

• 确认神经元中心C_i
• 利用BP算法调参

（2）ART网络：竞争型学习的重要代表
竞争学习是神经网络中一种常见的无监督学习，网络的输出神经元相互竞争，每一时刻只有一个竞争神经元被激活，其他神经元被抑制，胜者通吃。
最简单的竞争方法是：计算输出向量与每一个识别层神经元对应的模式类代表向量之间的距离，距离最小的获胜，将两类之间的相似度与误差阈值比较。

（3）SOM网络，竞争学习型无监督网络
将高维输入数据映射到低维空间（通常为二维空间），同时保持输入数据在高维空间的拓扑关系。
训练过程：在接受一个训练样本后，每个输出神经元会计算样本与自身携带的权向量之间的距离，距离最近的神经元获胜，然后最佳匹配的神经元及其相邻单元的权向量会被调整

（4）级联相关网络，结构自适应网络的重要代表
结构自适应网络：将网络结构也作为学习目标的一种，一起在训练过程中找到最符合数据特点的网络结构。

（5）Elman网络，递归神经网络
允许网络中出现环形结构，然一些神经元的输出反馈回来作为输入信号。

（6）Boltzmannn机，基于能量的模型
能量：为网络状态定义的一个名词，能量最小化时网络达到最佳状态。