数据结构学习——线性表的顺序表示及实现

线性表的顺序表示及实现

基本概念

顺序存储：把逻辑上相邻的数据元素存储在物理上相邻的存储单元中，占用一片连续的存储空间，知道某个元素的存储位置就可以计算其他元素的存储位置（即随机存取）

1. 顺序表中元素存储位置的计算
   若每个元素占用l个存储单元，且已知第i个数据元素（这里的i是逻辑位置）的存储位置，则第i+1个元素的存储位置：Loc(ai+1) = Loc(ai) + l；
   则Loc(ai) = Loc(a1) + (i-1)*l
2. 顺序表特点
   以物理位置相邻表示逻辑关系；
   任一元素均可以随机存取；
   插入和删除需要大量挪动元素

存储表示

1. 静态分配

#define size 100
typedef struct{
ElemType elem[size];	
int length;
}SqList;

2. 动态分配

typedef struct{
ElemType *data;	
int length;
}SqList;
SqList L;
L.data = (ElemType*)malloc(sizeof(ElemType)*size);		
//开辟内存空间，返回首地址
//释放用free(p)
//在c++中分配用new，释放用delete：
int *p = new int[size];

顺序表的操作

1.查找（按值查找）

在线性表L中查找与指定值e相同的第一个数据元素的位置
算法分析：
平均查找长度ASL：与给定值进行比较的关键字的个数的期望值
ASL = 1/n * (1+2+…+n) = (n+1)/2
时间复杂度为O(n)
空间复杂度O(1)

2.插入算法

在表的第i（1≤i≤n+1）个位置上，插入一个新节点e，使长度为n的线性表变成长度为n+1的线性表
算法思想：

①判断插入位置i是否合法
逻辑位置：1到n+1 物理下标：0到n
②判断顺序表的存储空间是否已满 L.length = maxSize
③将第n至第i位置的元素依次向后移动一个位置，空出第i个位置
④将要插入的新元素e放入第i个位置
⑤表长加一

算法分析：
主要耗费在移动元素的操作上
平均移动次数 = 1/(n+1) * (1+2+…+n) = n/2
时间复杂度为O(n)
空间复杂度O(1)

算法实现：

//插入  在第loc个结点前插入新元素  插入范围为1到n+1 
int insertElem(LinkList &l, int loc, int e){
	//1.找到第loc-1个结点  范围为0到n
	LNode *p = l;
	int j = 0;
	while(p && j<loc-1){
		p = p->next;
		j++;
	}
	if(!p || j>loc-1) return error;//位置不合法
	//2.生成新结点
	LNode *s = new LNode;
	s->data = e;
	//3.插入进链表
	s->next = p->next;
	p->next = s;
	return ok;
}

3.删除算法

将表的第i（1≤i≤n）个结点删除，使长度为n的线性表变成长度为n-1的线性表
算法思想：

①判断删除位置i是否合法
逻辑位置：1到n 物理下标：0到n-1
②将第i+1至第n位元素依次向前移动一个位置
③表长减一

算法分析：
主要耗费在移动元素的操作上
平均移动次数 = 1/n * (1+2+…+n-1) = (n-1)/2
时间复杂度O(n)
空间复杂度O(1)

算法实现：

//删除  删除第loc个结点，并返回删除的元素值  删除范围为1到n
int deleteElem(LinkList &l, int loc){
	//1.找到第loc-1个结点  范围为0到n-1 
	LNode *p = l;
	int j = 0;
	while(p->next && j<loc-1){
		p = p->next;
		j++;
	}
	if(!(p->next) || j>loc-1) return error;//位置不合法
	//2.删除结点q
	LNode *q = p->next;
	p->next = q->next;
	int e = q->data;
	delete q;
	return e;
}

整合代码完整cpp

示例输出：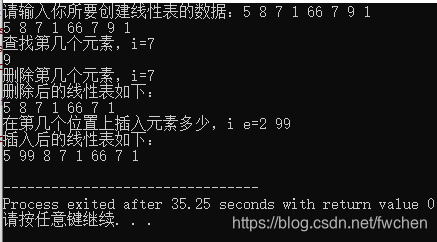

#include<iostream>
#include<vector>
using namespace std;
#define maxSize 100
#define ok 1
#define error -1

typedef struct{
	int *data;	//动态分配
	int length;
}SqList;

int initList(SqList &l){
	l.data = new int[maxSize];
	l.length = 0;
	return ok;
}

int destroyList(SqList &l){
	delete[] l.data;
	return ok; 
} 

int clearList(SqList &l){
	l.length = 0;
	return ok;
}
//返回第loc位置的元素值 loc指逻辑位置，不是下标 
int getElem(const SqList &l, int loc){
	//1.判断查找位置是否符合规范  1 ≤loc ≤length
	if(loc<1 || loc>l.length) return error;
	//2.返回该位置的元素值
	return l.data[loc-1]; 
}
//将元素插入到第loc位置上 
int insertElem(SqList &l, int loc, int e){
	//1.判断插入位置是否符合规范 1 ≤loc ≤length+1
	if(loc<1 || loc>l.length+1)	return error;
	//2.判断是否已满
	if(l.length == maxSize)	return error;
	//3.插入位置及后面的元素依次后移  移动后的下标范围：loc ≤i ≤length
	for(int i = l.length; i >= loc; i--){
		l.data[i] = l.data[i-1];
	}
	//4.插入元素
	l.data[loc-1] = e; 
	//5.表长加一
	l.length++;
	return ok; 
}
//将第loc位置上的元素删除，并返回该位置上的值 
int deleteElem(SqList &l, int loc){
	//1.判断待删除的元素位置是否符合规范  1 ≤loc ≤length
	if(loc<1 || loc>l.length) return 0;
	//2.获取待删除元素
	int e = l.data[loc-1];
	//3.将第loc位置后面的元素依次往前移动  移动后的下标范围：loc-1 ≤i ≤length-2
	for(int i = loc-1; i <= l.length-2; i++){
		l.data[i] = l.data[i+1];
	} 
	//4.表长减一
	l.length--;
	return e; 
}
//创建顺序表 
int createList(SqList &l){
	initList(l); 
	int e, i = 1; 
	while(1){
		cin >> e;
		insertElem(l, i++, e);
		if(cin.get() == '\n') break;
	}
	return ok;
}
//输出线性表
int printList(const SqList &l){
	for(int i = 0; i < l.length; i++)
		cout << l.data[i] << " ";
	cout << endl; 
	return ok;
} 
int main(){
	//创建线性表 
	cout << "请输入你所要创建线性表的数据："; 
	SqList l;
	initList(l);
	createList(l);
	printList(l);
	//根据元素的逻辑位置查找元素
	int i;
	cout << "查找第几个元素，i=";
	cin >> i;
	cout << getElem(l, i) << endl; 
	//删除元素 
	cout << "删除第几个元素，i=";
	cin >> i;
	deleteElem(l, i);
	cout << "删除后的线性表如下：\n";
	printList(l);
	//插入元素
	int e;
	cout << "在第几个位置上插入元素多少，i e=";
	cin >> i >> e;
	insertElem(l, i, e);
	cout << "插入后的线性表如下：\n";
	printList(l);
	return 0;
}