论文笔记：《DeepGBM: A Deep Learning Framework Distilled by GBDT for Online Prediction Tasks》

这篇文章涉及比较多的知识点：
1.阐述了树模型以及神经网络模型的优缺点，各自适合的场景和优势；
2.蒸馏技术：一个巧妙的地方就是，我们知道神经网络能够拟合各种函数，在这篇文章里并不是直接拟合树模型的输出，而是拟合树模型索引的输出，间接的得到树模型单位输出，从而在神经网络中学习到了树结构的知识。
3.用嵌入表示学习对众多的叶子节点降维，使得模型能够高效运行。

摘要

在线预测已经成为许多实际应用中最基本的任务之一。在线预测任务的两个典型且主要特点是在线数据呈表格空间形式和在线数据流形式。具体地，表格数据空间中存在着稀疏分类特征和密集数值特征，而在线数据流意味着具有潜在动态分布的连续任务生成的数据。因此，利用表格数据空间进行有效学习和快速适应在线数据流成为赢得在线预测的两个重要挑战。虽然梯度提升决策树（gbdt）和神经网络（nn）在实际中得到了广泛的应用，但它们都有各自的缺点。尤其是gbdt很难适应动态的在线数据流学习，而且在面对稀疏的分类特征时往往是无效的；而神经网络在面对稠密的数值特征时则很难获得令人满意的性能。本文提出了一种新的学习框架DEEPGBM，它综合了神经网络和gbdt的优点，使用了两个相应的神经网络组件：（1）catnn，重点处理稀疏的分类特征。（2）GBDT2NN，利用GBDT2NN提取的知识，重点研究密集的数值特征。在这两个组件的支持下，deepgbm可以同时利用分类和数值特性，同时保持高效在线更新的能力。对各种公开数据集的综合实验表明，deepgbm在各种在线预测任务中都能优于其他公认的基线算法。

1. 简介

在线预测是指在许多实际工业应用中起着重要作用的一类任务，如广告搜索中的点击预测、web搜索中的内容排序、推荐系统中的内容优化、交通规划中的行程时间估计等。
一个典型的在线预测任务通常存在着表格数据空间和在线数据流两个特定的特征。特别地，表格数据空间意味着在线预测任务的输入特征可以包括分类和数值表格特征。例如，广告搜索中点击预测任务的特征空间通常包含广告类别等分类特征空间，以及查询与广告文本相似性等数字特征空间。在线数据生成意味着这些任务的实际数据是在线生成的，并且数据分布可以实时动态。例如，新闻推荐系统可以实时生成大量的数据，不断涌现的新闻可以在不同的时间产生动态的特征分布。
因此，要寻求一个有效的基于学习的在线预测模型，就必须解决两个主要的挑战：（1）如何学习一个具有表格输入空间的有效模型；（2）如何使模型适应在线数据生成。目前，两类机器学习模型被广泛应用于在线预测任务的求解，即梯度提升决策树（gbdt）和神经网络（nn）。不幸的是，它们都不能同时很好地应对这两个主要挑战。换言之，当用于解决在线预测任务时，gbdt或nn都会产生各自的优缺点。
一方面，gbdt的主要优势在于它能够有效地处理密集的数值特征。由于gbdt可以迭代地选取统计信息增益最大的特征来构建树，因此它可以自动地选择和组合有用的数值特征，以更好地适应训练目标。这就是gbdt在点击预测(CTR)、web搜索排名和其他公认的预测任务中展示其有效性的原因。同时，gbdt在在线预测任务中有两个主要的弱点。首先，由于gbdt中学习到的树是不可微的，所以在在线模式下更新gbdt模型是很困难的。频繁地从头到尾的训练模型使得gbdt在学习在线预测任务时效率很低。此外，这一弱点还阻碍了gbdt对超大规模数据的学习，因为将大量数据加载到内存中进行学习通常是不切实际的。
gbdt的第二个弱点是它在稀疏分类特征上的学习效率低下。特别是将分类特征转换成稀疏高维的独热(one-hot)编码后，稀疏特征的统计信息增益将变得非常小，因为稀疏特征对不平衡分割的增益几乎与非分割相同。因此，gbdt不能有效地利用稀疏特征来生长树。尽管还有一些分类编码方法可以直接将分类值转换为密集的数值，但由于不同分类的编码值可能相似，难以区分它们，因此这些方法会损害原始信息。通过枚举可能的二进制分区，分类特征也可以直接用于树学习，然而，这种方法在分类特征稀疏的情况下往往会对训练数据过度拟合，因为每一类数据太少，统计信息有偏差。简言之，虽然gbdt可以很好地学习密集的数值特征，但两个弱点，即难以适应在线数据生成和学习稀疏分类特征的无效性，导致gbdt在许多在线预测任务中失败，特别是那些需要在线调整模型和包含许多稀疏分类特征的模型。
另一方面，神经网络的优势在于它对在线任务中大规模数据的有效学习，因为批处理模式的反向传播算法，以及它对稀疏分类特征的学习能力，通过公认的嵌入结构(embedding)。最近的一些研究表明，神经网络在包括点击预测和推荐系统在内的在线预测任务中的应用是成功的，然而，神经网络的主要挑战在于它在学习稠密的数值表格特征方面的不足。全连接神经网络（fcnn）虽然可以直接用于稠密的数值特征，但由于其全连接的模型结构导致了非常复杂的优化超平面，很容易陷入局部最优，因此常常导致性能不理想。因此，在许多具有稠密数值表特征的任务中，神经网络往往不能优于gbdt。综上所述，尽管神经网络能够有效地处理稀疏的分类特征，并且能够有效地适应在线数据流，但是通过学习稠密的数值表格特征仍然很难得到有效的模型。

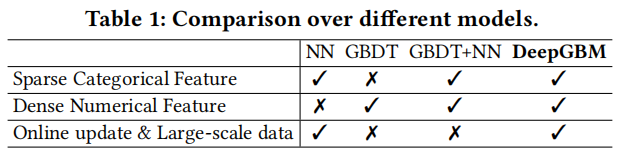
如表1所示，神经网络(NN)或梯度提升树(gbdt)在获得在线预测任务的模型方面都有其优缺点。直观地说，探索如何将神经网络和gbdt的优点结合起来，同时解决在线预测任务中的两大挑战，即表格数据空间和在线数据流生成，将是非常有益的。
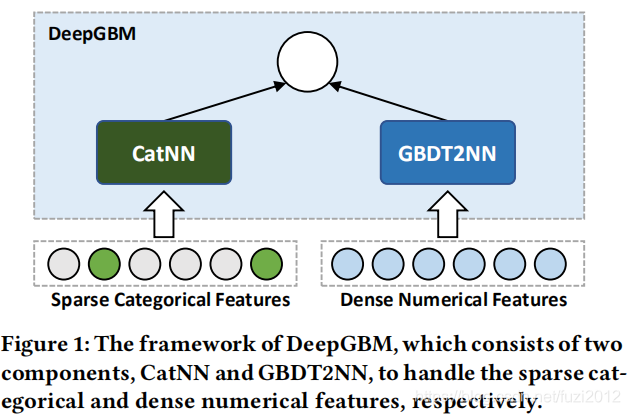
文章中提出了一种新的学习框架deepgbm，它将神经网络和gbdt相结合，以获得一个更有效的通用在线预测任务模型。特别是，如图1所示，整个deepgbm框架由两个主要部分组成：catnn是一个输入分类特征的神经网络(NN)结构，gbdt2nn是另一个输入数值特征的神经网络(NN)结构。为了充分利用gbdt在学习数值特征方面的优势，gbdt2nn尝试将gbdt学习到的知识提取为神经网络建模过程。具体来说，为了提高知识提取的有效性，gbdt2nn不仅传递了预先训练的gbdt的输出知识，而且还融合了所得到的树结构所隐含的特征重要性和数据划分知识(特征选择和特征生成)。这样，在达到与gbdt相当的性能的同时，采用神经网络结构的gbdt2nn在面对在线数据生成时，可以很容易地通过不断涌现的数据进行更新。
deepgbm由两个基于神经网络的组件catnn和gbdt2nn提供支持，在保持高效在线学习的重要能力的同时，确实可以在类别和数值特征上产生强大的学习能力。为了说明所提出的deepgbm的有效性，我们使用表格数据对各种公开可用的数据集进行了广泛的实验。综合实验结果表明，在各种预测任务中，deepgbm的性能优于其他方案。
总之，本文的贡献是多方面的：
• 提出了deepgbm结合gbdt和nn的优点，在保留有效在线更新能力的同时，利用分类和数值特征，对各种具有表格数据的预测任务进行更新。
• 提出了一种有效的解决方案，通过考虑gbdt模型学习树中选择的输入、结构和输出知识，将gbdt模型的学习知识提取为神经网络模型。
• 广泛的实验表明，deepgbm是一种现成的模型，可以用于各种预测任务，并实现最先进的性能.

2. DEEPGBM

在这一部分中，将详细阐述新提出的学习框架deepgbm如何将nn和gbdt集成在一起，以获得更有效的通用在线预测任务模型。具体地说，如图1所示，整个deepgbm框架由两个主要部分组成：catnn是一个输入类别特征的神经网络结构，gbdt2nn是另一个从gbdt中提炼出来的神经网络结构，侧重于学习密集的数值特征。

2.1 CatNN 专注于稀疏类别特征(for Sparse Categorical Features)

为了解决在线预测问题，神经网络被广泛应用于学习分类特征的预测模型，如wide&deep(广度与深度)、pnn、deepfm和xdeepfm。由于CATNN的目标是与这些算法相同的，可以直接利用现有的任何成功的神经网络结构发挥CATNN的功能，而不重新造车轮。特别是与以往的工作一样，catnn主要依靠嵌入(embedding)技术，能够有效地将高维稀疏向量转化为稠密向量。此外，本文还利用fm组件和deep组件来学习特征上的交互。请注意，catnn不受这两个组件的限制，因为它可以使用具有类似功能的任何其他nn组件。
嵌入是高维稀疏向量的低维密集表示，可以表示为:

$$E_{V_i}(x_i)=embedding\_lookup(V_i,x_i)\text{\hspace{1em}(1)}$$
其中$x_i$表示第$i$个特征的值 ，$V_i$存储第i个特征的所有嵌入表示(embedding representation)，可以通过反向传播来学习，$E_{V_i}(x_i)$将返回对应的$x_i$嵌入向量。基于此，我们可以使用FM组件来学习线性(linear)特征和成对特征(pair-wise)交互，并可以表示为

$$y_{FM}(x)=w_0+⟨w,x⟩+\sum _{i=1}^d\sum _{j=i+1}^d⟨E_{V_i}(x_i),E_{V_j}(x_j)⟩x_i{x}_j\text{\hspace{1em}(2)}$$

其中$d$是特征数，$w_0$和$w$是线性部分的参数，$⟨.,.⟩$是内积运算。然后，使用deep组件学习高阶特征交互：

$$y_{Deep}(x)=N([E_{V_1}(x_1{)}^T,E_{V_2}(x_2{)}^T,...,E_{V_2}(x_2{)}^T{]}^T;\theta )\text{\hspace{1em}(3)}$$

其中$N(x;\theta )$是具有输入$x$和参数$\theta$的多层神经网络模型。结合两个组件，catnn的最终输出是

$$y_{Cat}(x)=y_{FM}(x)+y_{Deep}(x)\text{\hspace{1em}(4)}$$

2.2 GBDT2NN 专注于数值密集型特征(for Dense Numerical Features)

在本小节中，具体描述如何将gbdt中学习到的树提取(distill)为神经网络模型的细节。简单起见，首先介绍如何将单棵树提取为神经网络。然后再将这一思想推广到gbdt中的多树蒸馏。

2.2.1 单树知识提取(Single Tree Distillation)

传统的知识蒸馏(Distillation)方法大多都是只根据所学的函数传递模型的知识，以确保新模型产生的输出与传递的模型输出相似。然而，由于树模型与神经网络的本质不同，除了传统的模型蒸馏方法外，树模型中的更多知识可以被提取并转化为神经网络的所具备的能力。树模型除了函数的输出之外，还有其他更为重要的知识：特别是学习树中的特征选择和特征重要性提取，以及学习树结构所隐含的数据划分能力。
树的特征选择能力 (Tree-Selected Features). 与神经网络相比，基于树的模型的一个特点是不使用所有的输入特征，因为它的学习会根据统计信息贪婪地选择适合训练目标的有用特征。因此，根据树选择出来的特征来传递这些知识，可以仅仅使用树选择出来的特征作为神经网络的输入，以提高神经网络模型的学习效率，而不是使用所有的输入特征。形式上，定义${\mathbb{I}}^t$为树$t$中使用的特征的索引。那么用$x[{\mathbb{I}}^t]$作为神经网络的输入。
树型结构知识(Tree Structure).从本质上讲，决策树的树结构知识是指如何将数据划分成多个不重叠的区域（叶），即将数据聚类成不同的类，同一叶中的数据属于同一类。这种树结构很难直接转化为神经网络，因为它们从结构上有着明显的区别。所幸的是，神经网络已经被证明足以逼近任何函数，所以可以使用神经网络模型来逼近树结构的函数输出，并实现结构知识的蒸馏。因此，如图2所示，可以使用神经网络来拟合树生成的聚类结果，从而使神经网络逼近决策树的结构函数。

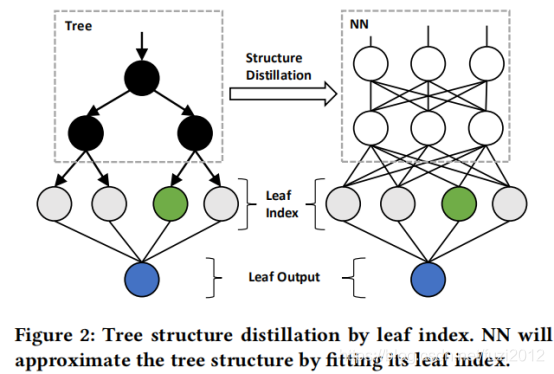
形式上，把树$t$表示为$C^t(x)$的结构函数，它返回样本的输出叶子索引，即树生成的聚类结果。然后，可以使用神经网络模型来逼近结构函数$C^t(.)$，学习过程可以表示为：
$$mi{n}_{\theta }\frac{1}{n}\sum _{i=1}^n{\mathfrak{L}}^{\prime }(N(x^i[{\mathbb{I}}^t];\theta ),L^{t,i})\text{\hspace{1em}(5)}$$

其中$n$是训练样本的数目，$x^i$是第$i$个训练样本，$L^{t,i}$是样本$x^i$的树$C^t(x^i)$叶子输出的独热(one-hot)表示，${\mathbb{I}}^t$是树$t$中使用的特征的索引，$\theta$是神经网络模型$N$的模型参数，可以通过反向传播更新，${\mathfrak{L}}^{\prime }$是交叉熵之类的多分类问题的损失函数。因此，在学习之后，就可以得到一个神经网络模型$N(.;\theta )$。由于神经网络具有很强的表达能力，经过学习的神经网络模型应该能完美地逼近决策树的结构函数。
树叶子值的输出(Tree Outputs).由于在前面的步骤中学习了从树输入到树结构的映射，所以要提取树的输出，只需要知道从树结构到树输出的映射。在决策树中叶子索引有相应的叶子值，因此实际上不需要学习此映射。将树$t$的叶子值表示为$q^t$，那么$q_i^t$表示第$i$个叶子的叶子值。要得到树模型的输出，只需要用$p^t=L^t\times q^t$将$L^t$映射到树的值输出。
结合上述的单树蒸馏方法，从$t$树蒸馏得到的神经网络的输出可以表示为
$$y^t(x)=N(x[{\mathbb{I}}^t];\theta )\times q^t\text{\hspace{1em}(6)}$$

2.2.2 多棵树知识提取(Multiple Tree Distillation)

由于gbdt中有多棵树，结合以上的单树蒸馏方法，应从单棵树推广多棵树的蒸馏方法。一个最直接的解决方案是使用多个神经网络模型对应多个树模型，每个模型都是从一棵树中提取出来的。然而，由于结构蒸馏目标的高维，复杂度$o（L\times nn）$，该方法效率很低。为了提高效率，本文提出了叶子嵌入蒸馏法和树分组法，分别降低了叶子的个数$L$和神经网络模型的个数$nn$。

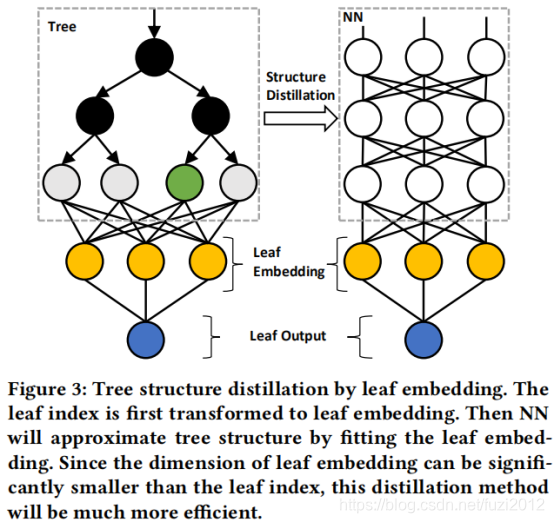
叶子嵌入蒸馏(Leaf Embedding Distillation).如图3所示，采用嵌入技术来降低结构蒸馏目标$L$(叶子的个数)的维数，在该步骤中利用树模型自身的信息进行再训练。更具体地说，由于叶子索引和叶子值之间存在双射关系，因此可以使用叶子值来学习嵌入。形式上，嵌入的学习过程可以表示为

$$mi{n}_{w,w_0,{\omega }^t}\frac{1}{n}\sum _{i=1}^n{\mathfrak{L}}^{\prime \prime }(w^{T}H(L^{t,i};{\omega }^t)+w_0,p^{t,i})\text{\hspace{1em}(7)}$$

其中$H^{t,i}=H(L^{t,i};{\omega }^t)$是以${\omega }^t$为参数的一层全连接网络，主要能把one_hot的输入$L^{t,i}$(叶子索引)转化成密集的嵌入表示H^{t,i}，$p^{t,i}$为样本在树中的叶子节点的预测值，${\mathfrak{L}}^{\prime \prime }$是树学习过程中的损失函数，$w$和$w_0$是用于将嵌入映射到叶子节点值的参数。完了之后，可以改用密集嵌入$H^{t,i}$作为目标来逼近树结构的函数，而不是稀疏高维的独热表示$L$。这个新的学习过程可以表示为
$$mi{n}_{\theta }\frac{1}{n}\sum _{i=1}^n\mathfrak{L}(N(x^i[{\mathbb{I}}^t];\theta ),H^{t,i})\text{\hspace{1em}(8)}$$

其中$\mathfrak{L}$是拟合密集嵌入的回归损失，如 $L2$ 损失。由于$H^{t,i}$的维数要比one-hot的$L$小得多，因此叶节点嵌入蒸馏在多树蒸馏中更为有效。因为它将使用更少的神经网络参数，因此会效率会更高。
树分组法(Tree Grouping).为了减少神经网络个数$nn$，可以对树进行分组，然后对分组后的树用神经网络模型去蒸馏知识。但是分组有两个问题(1)怎么去对这些树进行分组，(2)怎么去对这些分组后树组进行蒸馏。
首先，对于分组策略，有很多解决方案。例如随机分组、等顺序分组、基于重要性或相似性的分组等。在本文中，使用等随机分组。假设有$m$棵树，想把它们分成$k$组，每组中有$s=\lceil m/k\rceil$树,第$j$组中的树是${\mathbb{T}}_j$，它包含来自gbdt的随机s棵树。其次，为了从多棵树中提取，可以扩展到多棵树的叶子索引嵌入蒸馏技术。给定一组树$\mathbb{T}$，扩展等式(7)从多个树学习叶子节点的嵌入表示。
$$mi{n}_{w,w_0,{\omega }^{\mathbb{T}}}\frac{1}{n}\sum _{i=1}^n{\mathfrak{L}}^{\prime \prime }(w^{T}H(|{|}_{t\in \mathbb{T}}(L^{t,i});{\omega }^{\mathbb{T}})+w_0,\sum _{t\in \mathbb{T}}{p}^{t,i})\text{\hspace{1em}(9)}$$

其中||(.)是拼接操作(concatenate operation)，$G^{\mathbb{T},i}=H(|{|}_{t\in \mathbb{T}}(L^{t,i});{\omega }^{\mathbb{T}})$是一个一层全连通网络，它将多个单树叶子索引向量的拼联，转化为$\mathbb{T}$树中的密集嵌入$G^{\mathbb{T},i}$，然后用新的嵌入作为神经网络模型的蒸馏目标，其学习过程可以表示为
$${\mathfrak{L}}^{\mathbb{T}}=mi{n}_{{\theta }^{\mathbb{T}}}\frac{1}{n}\sum _{i=1}^n\mathfrak{L}(N(x^i[{\mathbb{I}}^{\mathbb{T}}]),G^{\mathbb{T},i})\text{\hspace{1em}(10)}$$
其中${\mathbb{I}}^{\mathbb{T}}$是树分组$\mathbb{T}$中用到的特征。当树分组$\mathbb{T}$中的树的数量较大时，${\mathbb{I}}^{\mathbb{T}}$可能包含很多特征，从而影响树模型的特征选择能力。因此，只根据特征的重要性在${\mathbb{I}}^{\mathbb{T}}$其中使用重要性较高的特征。综上所述，结合上述方法，从树组$\mathbb{T}$中提取神经网络模型的最终输出是
$$y_{\mathbb{T}}(x)=w^T\times N(x[{\mathbb{I}}^{\mathbb{T}}];{\theta }^{\mathbb{T}})+w_0\text{\hspace{1em}(11)}$$

包含k个树组的gbdt模型的输出是
$$y_{GBDT2NN}(x)=\sum _{j=1}^k{y}_{{\mathbb{T}}_j}(x)\text{\hspace{1em}(12)}$$

综上所述，由于叶子嵌入蒸馏和树分组，gbdt2nn可以有效地将gbdt中的许多树提取为一个紧凑的神经网络模型。而且除了树的模型值输出，树的特征选择和结构知识也被有效地提取到神经网络模型中。

2.3 DeepGBM模型的训练(Training for DeepGBM)

deepgbm模型的训练，包括如何在离线状态下对其进行端到端训练，以及如何高效地在线更新它。

2.3.1 端到端的离线训练 (End-to-End Offline Training)

为了训练deepgbm，首先需要使用离线数据训练gbdt模型，然后使用等式（9）得到gbdt中树的叶子节点嵌入表示。然后就可以端到端地训练deepgbm。将deepgbm的输出表示为
$$\hat{y}(x)={\sigma }^{\prime }(w_1\times y_{GBDT2NN}(x)+w_2\times y_{Cat}(x))\text{\hspace{1em}(13)}$$
其中$w_1$和$w_2$是用于组合gbdt2nn和catnn的可训练参数，σ′是输出变换函数，例如用于二进制分类的sigmoid。然后，可以使用下面的损失函数进行端到端的训练
$${\mathfrak{L}}_{offline}=\alpha {\mathfrak{L}}^{\prime \prime }(\hat{y}(x),y)+\beta \sum _{j=1}^k{\mathfrak{L}}^{{\mathbb{T}}_j}\text{\hspace{1em}(14)}$$

其中$y$是样本$x$的训练目标，${\mathfrak{L}}^{\prime \prime }$是分类任务的交叉熵等相应任务的损失函数，${\mathfrak{L}}^{\mathbb{T}}$是树组$\mathbb{T}$的嵌入损失，并在等式(10)中定义，k是树组个数，α和β是预先给定的用于控制端到端损失强度和嵌入损耗的超参数。

3.3.2 在线更新(Online Update)

由于gbdt模型是离线训练的，在在线更新中嵌入学习(embedding learning)会影响在线时效性。因此，在在线更新模型的时候不再包含${\mathfrak{L}}^{\mathbb{T}}$，在线更新模型的时候，损失函数表示成：
$${\mathfrak{L}}_{online}={\mathfrak{L}}^{\prime \prime }(\hat{y}(x),y)\text{\hspace{1em}(15)}$$

它只使用端到端的损失。因此，当使用deepgbm在线时，我们只需要新的数据来通过${\mathfrak{L}}_{online}$更新模型，而不需要涉及gbdt和从头开始的再训练模型。简而言之，deepgbm将非常有效地执行在线任务。此外，它还可以很好地处理稠密的数值特征和稀疏的分类特征。

---

本文为潘振福原创的博客，已独家授权公众号【浅梦的学习笔记】发布在微信公众平台。
本文链接: link.