增量(incremental)方法
在排好子数组A[1⋯j−1]A[1\cdots j-1]A[1⋯j−1]后将元素a[j]a[j]a[j]插入,形成排好序的子数组A[1⋯j]A[1\cdots j]A[1⋯j]
Input: sequence a1,a2,⋯ ,ana_1,a_2,\cdots,a_na1,a2,⋯,an of numbers
Output: <a1′,a2′,⋯ ,an′>  ,  ai′<aj′  (i<j)<a'_1,a'_2,\cdots,a'_n>\;,\; a'_i<a'_j \;(i<j)<a1′,a2′,⋯,an′>,ai′<aj′(i<j)
插入排序

从第2开始在子序列a1,a2,⋯ ,aja_1,a_2,\cdots,a_ja1,a2,⋯,aj中,将aja_jaj插入到合适的位置(左边的比它小,右边的比它大).
**循环不变量(loop invariant)**的作用是证明程序的正确性。可理解为数学归纳法中的假设。在上面的算法中,我们要证明数列{A[j]}j=1n\{ A[j] \}_{j=1}^n{A[j]}j=1n是升序排列.
证明:
循环不变量:在每一轮迭代开始,子数组A[1,⋯ ,j−1]A[1,\cdots ,j-1]A[1,⋯,j−1]中包含了最初位于A[1,⋯ ,j−1]A[1,\cdots ,j-1]A[1,⋯,j−1],但目前已经排好序的各个元素.
j=2j=2j=2时,子数组A[1]A[1]A[1]满足循环不变量的定义.
假设j=kj=kj=k时成立,下证j=k+1j=k+1j=k+1时成立:易得……
当j=nj=nj=n时,因为……也成立。
综上所述,该算法是正确的.
To use a loop invariant to prove correctness, we must show three things about it:
Initialization: It is true prior to the first iteration of the loop.
Maintenance: If it is true before an iteration of the loop, it remains true before the next iteration.
Termination: When the loop terminates, the invariant usually along with the reason that the loop terminated gives us a useful property that helps show that the algorithm is correct.
算法的运行时间

第一行时间为nnn,因为跳出循环程序还需要运行一次。第二行是因为已经跳出循环了,所以只要n−1n-1n−1次.
其中tjt_jtj等于while循环所做的测试次数,即当 jjj 固定以后,while循环需要测试 j−1j-1j−1 个数据.
运行总时间T(n)=c1n+c2(n−1)+c4(n−1)+c5∑j=2ntj+c6∑j=2n(tj−1)+c7∑j=2n(tj−1)+c8(n−1)T(n)=c_1n+c_2(n-1)+c_4(n-1)+c_5\sum_{j=2}^nt_j+c_6\sum_{j=2}^n(t_j-1)+c_7\sum_{j=2}^n(t_j-1) +c_8(n-1)T(n)=c1n+c2(n−1)+c4(n−1)+c5j=2∑ntj+c6j=2∑n(tj−1)+c7j=2∑n(tj−1)+c8(n−1)
- 最好的情况
第5行当A[j−1]≤A[j]A[j-1] \le A[j]A[j−1]≤A[j]时,对每个jjj来说,第五行只执行一次,并且第6,7行不执行.
Tbestn=c1n+c2(n−1)+c4(n−1)+c5(n−1)+c8(n−1)T_{best}^n=c_1n+c_2(n-1)+c_4(n-1)+c_5(n-1)+c_8(n-1)Tbestn=c1n+c2(n−1)+c4(n−1)+c5(n−1)+c8(n−1)
=(c1+c2+c4+c5+c8)n−+(c2+c4+c5+c8)=an+b=(c_1+c_2+c_4+c_5+c_8)n-+(c_2+c_4+c_5+c_8)=an+b=(c1+c2+c4+c5+c8)n−+(c2+c4+c5+c8)=an+b - 最坏的情况
Tworstn=c1n+c2(n−1)+c4(n−1)+c5(1+n−1)(n−1)2+c6n(n−1)2+c7n(n−1)2+c8(n−1)T_{worst}^n=c_1n+c_2(n-1)+c_4(n-1)+c_5\frac{(1+n-1)(n-1)}{2}+c_6\frac{n(n-1)}{2}+c_7\frac{n(n-1)}{2}+c_8(n-1)Tworstn=c1n+c2(n−1)+c4(n−1)+c52(1+n−1)(n−1)+c62n(n−1)+c72n(n−1)+c8(n−1)
=an2+bn+c=an^2+bn+c=an2+bn+c
分治法(divide and conquer)
分治策略:将原问题划分为nnn个规模较小而结构与原问题相似的子问题;递归地解决这些子问题,然后再合并器结果,就得到原问题的解
时间复杂度:假设T(n)T(n)T(n)为一个规模为nnn的问题的运行时间。如果把问题分得足够小,如n≤cn \le cn≤c(ccc),则得到直接解的时间常量,写作Θ(1)\Theta(1)Θ(1)。假设我们把原问题分解为aaa个子问题,每个问题的大小是原问题的1b\frac{1}{b}b1。如果分解问题和合并问题的时间分别是D(n)  ,  C(n)D(n)\;,\;C(n)D(n),C(n)则得到递归式
T(n)={Θ(1)  ,  n≤caT(n/b)+D(n)+C(n) T(n)=\begin{cases} \Theta(1) \;,\; n \le c \\ aT(n/b)+D(n)+C(n) \end{cases} T(n)={Θ(1),n≤caT(n/b)+D(n)+C(n)
合并排序(merge sort)
对数组A[p⋯r]A[p\cdots r]A[p⋯r]进行排序。将数组分成两半:A[p⋯q]A[p \cdots q]A[p⋯q]和A[q+1⋯r]A[q+1 \cdots r]A[q+1⋯r]


前两行计算数组A[p⋯q]A[p \cdots q]A[p⋯q]和数组A[q+1⋯r]A[q+1 \cdots r]A[q+1⋯r]的长度;第3行到底7行将数组A[p⋯q]A[p \cdots q]A[p⋯q]复制到LLL,数组A[q+1⋯r]A[q+1 \cdots r]A[q+1⋯r]复制到RRR。for循环是要把排好序的数组L,RL,RL,R按照元素大小复制到数组AAA中。在这个过程中,我们需要判断数组LLL和RRR是否已经被搬空了,即指针走到了最后一位。所以我们将无穷大填到数组最后。由于我们需要对比两个数组中的元素,将小的那个放到数组AAA中。当有一个数组为空时,指针就会指向最后一位,即无穷大。因为任何数字都比无穷大小,所以该数组的指针不会再往后走了。
上述for循环的循环不变式:
子数组A[p⋯k−1]A[p \cdots k-1]A[p⋯k−1]包含了L[1⋯n1+1]L[1 \cdots n_1+1]L[1⋯n1+1]和R[1⋯n2+1]R[1 \cdots n_2+1]R[1⋯n2+1]中的k−pk-pk−p个最小的元素,并且是排好序的。
时间复杂度:
分解:计算向量中间位置,只需要常量时间.
解决:递归地解两个规模为n/2n/2n/2的子问题,时间为2T(n/2)2T(n/2)2T(n/2)
合并:merge算法的时间复杂度为c(n)=Θ(n)c(n)=\Theta(n)c(n)=Θ(n)
综上所以有:
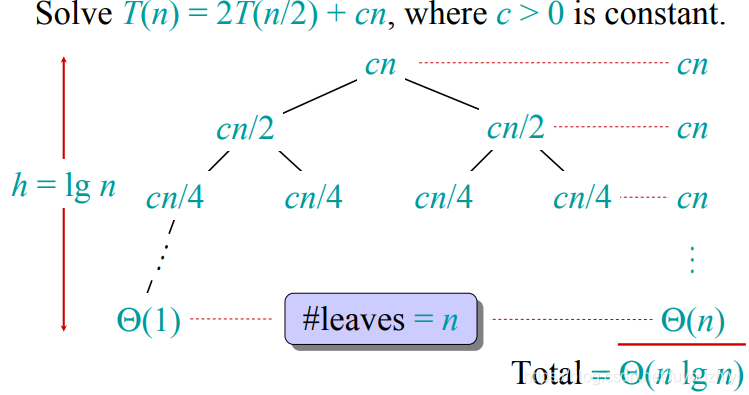
T(n)={Θ(1)  ,  n=12T(n/2)+cn  ,n>1 T(n)=\begin{cases} \Theta(1) \;,\; &n =1 \\ 2T(n/2)+cn \;, &n>1 \end{cases} T(n)={Θ(1),2T(n/2)+cn,n=1n>1
T(n)=nlog2n=nlgnT(n)=n\log_2n=n\lg nT(n)=nlog2n=nlgn




















 676
676

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








