摘要
在本文中,我们提出了一种基于迭代自训练(self-training)过程的新型UDA框架.该问题被形式化为潜在变量损失最小化,并且可以通过生成目标数据的伪标签和通着这些伪标签再训练来解决这些问题。在ST之上,我们还提出了一种新颖的类平衡自训练(CBST)框架,以避免大类在伪标签生成上的逐渐优势,并引入空间先验来细化生成的标签。综合实验表明,所提出的方法在多个主要UDA设置下实现了最先进的语义分割性能。
总结
-
每次生成置信度最高的伪标签,以保证最终迭代出正确的标签
-
空间先验信息——像素nnn是类别ccc的频率。用以辅助目标域的训练,减少错误
Loss 函数
minw,y^LS,P(w,y^)=−∑s=1S∑n=1Nys,nTlog(pn(w,Is))−∑t=1T∑n=1N∑c=1C[y^t,n(c)log(qn(c)pn(c∣w,It))+kcy^t,n(c)] \min_{\mathbf{w},\hat{\mathbf{y}}}\mathcal{L}_{S,P}(\mathbf{w},\hat{\mathbf{y}})=- \sum_{s=1}^S \sum_{n=1}^N \mathbf{y} ^T_{s,n} \log(\mathbf{p}_n(\mathbf{w},\mathbf{I}_s)) -\sum_{t=1}^T\sum_{n=1}^N \sum_{c=1}^C [\hat{y}_{t,n}^{(c)} \log( q_n(c) p_n(c|\mathbf{w},\mathbf{I}_t) )+k_c\hat{y}_{t,n}^{(c)}]w,y^minLS,P(w,y^)=−s=1∑Sn=1∑Nys,nTlog(pn(w,Is))−t=1∑Tn=1∑Nc=1∑C[y^t,n(c)log(qn(c)pn(c∣w,It))+kcy^t,n(c)]
s.t.  y^t,n=[y^t,n(1),⋯ ,y^t,n(C)]∈{{e∣e∈RC}∪0},  ∀t,n  ;kc>0,∀c s.t. \; \hat{\mathbf{y}}_{t,n}=[\hat{y}_{t,n}^{(1)},\cdots,\hat{y}_{t,n}^{(C)}] \in \{ \{ \mathbf{e}|\mathbf{e}\in \mathbb{R}^C \} \cup \mathbf{0} \} , \; \forall t,n \; ; k_c>0,\forall c s.t.y^t,n=[y^t,n(1),⋯,y^t,n(C)]∈{{e∣e∈RC}∪0},∀t,n;kc>0,∀c
- 第一项:使源域分类尽可能正确
- Is\mathbf{I}_sIs是源域中第sss个图片.
- ys,n\mathbf{y} _{s,n}ys,n 是一个N×1N \times 1N×1的向量,表示图片Is\mathbf{I}_sIs中第nnn个像素的ground truth,每张图有NNN个像素.
- w\mathbf{w}w是网络权重.
- log(pn(w,Is))\log(\mathbf{p}_n(\mathbf{w},\mathbf{I}_s))log(pn(w,Is)) 表示像素nnn 的类别概率.
- 第二项
- y^t,n\hat{\mathbf{y}}_{t,n}y^t,n 是目标域的伪标签.每次选择置信度最高的,最优可能正确的标签作为伪标签.当y^t,n=0\hat{\mathbf{y}}_{t,n}=0y^t,n=0时,忽略这个伪标签在模型训练中的作用.
- y^t,n(c)\hat{y}_{t,n}^{(c)}y^t,n(c):该像素是第ccc类的概率值 .
- kck_ckc:过滤掉概率值小于e−kce^{-k_c}e−kc的伪标签.对每一类kck_ckc值选取方法如下:

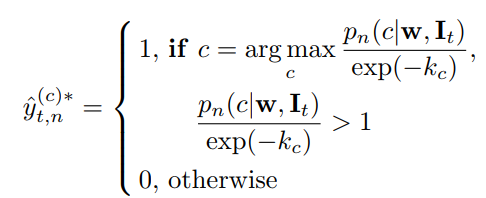
- qn(c)q_n(c)qn(c):像素nnn是类别ccc的频率。此为空间先验信息,并限制为∑i=1Nqn(c)=1\sum_{i=1}^N q_n(c)=1∑i=1Nqn(c)=1
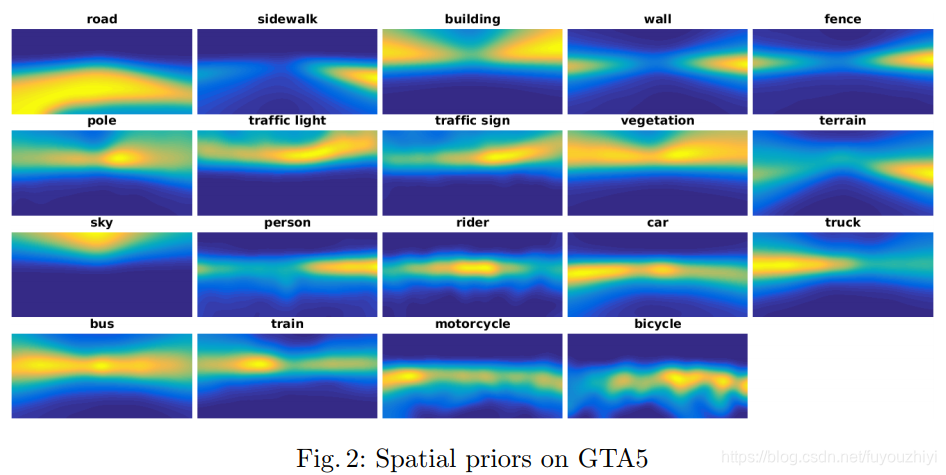
下图显示了空间先验信息的热度图,计算自GTA5数据集。黄色代表高能量,蓝色代表低能量。 - qn(c)pn(c∣w,It)q_n(c) p_n(c|\mathbf{w},\mathbf{I}_t)qn(c)pn(c∣w,It) :在网络参数为w\mathbf{w}w,图片是It\mathbf{I}_tIt的条件下类别为ccc的概率是pn(c∣w,It)p_n(c|\mathbf{w},\mathbf{I}_t)pn(c∣w,It). 乘以类别ccc在像素nnn的频率是加入先验信息。举个例子,对于图像左下角的像素,观察其热度图,我们知道类别为road的频率最大,sidewalk的频率小。如果给定一张图片左下角是road,但是伪标签y^t,n(c=road)\hat{y}_{t,n}^{(c=road)}y^t,n(c=road)的值很小,即不是road类。
举个例子,对于图像左下角的像素,观察其热度图,我们知道类别为road的频率最大,sidewalk的频率小。如果给定一张图片左下角是road,但是伪标签 y^t,n(c=road)\hat{y}_{t,n}^{(c=road)}y^t,n(c=road)的值很小,即不是road类。那么qn(c)pn(c∣w,It)q_n(c) p_n(c|\mathbf{w},\mathbf{I}_t)qn(c)pn(c∣w,It)的值接近0,即 −y^t,n(c)log(qn(c)pn(c∣w,It))-\hat{y}_{t,n}^{(c)} \log( q_n(c) p_n(c|\mathbf{w},\mathbf{I}_t) )−y^t,n(c)log(qn(c)pn(c∣w,It))会很大。当我们最小化Loss函数时,就能利用先验信息修正这个错误。





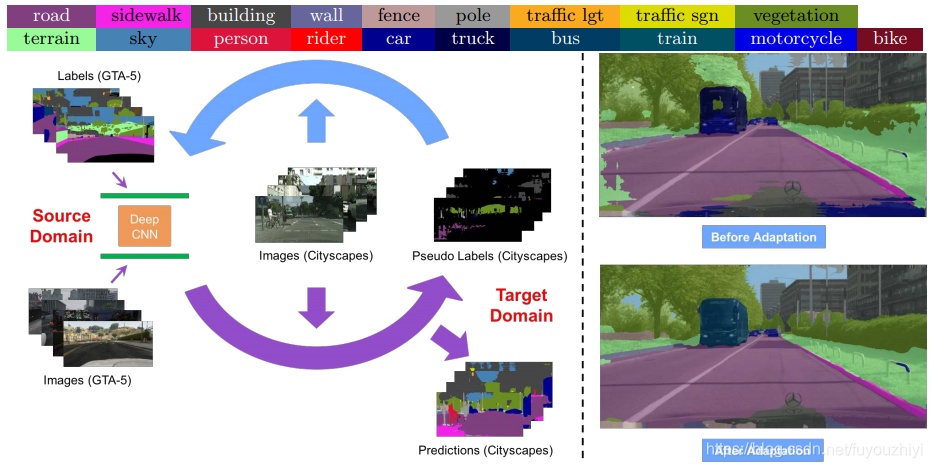
 介绍一种基于迭代自训练的UDA框架,通过生成目标数据的伪标签并结合空间先验信息优化标签,避免大类优势,实现语义分割任务的性能提升。
介绍一种基于迭代自训练的UDA框架,通过生成目标数据的伪标签并结合空间先验信息优化标签,避免大类优势,实现语义分割任务的性能提升。
















 3175
3175

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








