算法设计与分析实验报告（二）

实验二：斐波那契数列递归和非递归算法时间效率的实验验证

1.实验目的

通过比较斐波那契数列递归和非递归算法运算的时间，从而对比得出递归和循环的效率高低。

2.实验内容

分别实现求斐波那契数列第N个数的递归和非递归算法，并记录下随着问题规模N从小到大变化过程中两个算法实现的运行时间，分析其中的规律，并得出分析结论。要求在实验报告中贴出测试实例的运行窗口，并制作一个表格呈现N变化时两个算法实现的运行时间，以文字形式进行分析并得出结论。

3.设计思路

使用递归方式计算斐波那契数时，第n项总是须要先计算出第n-1项和第n-2项，运行时间T(N)T(N-1)+T(N-2)。由于T(N)作为斐波那契数满足同样的递推关系并具有相同的初始条件，因此，T(N)事实上是以斐波那契数相同的速度增长而指数级增长。

循环求斐波那契只须要记录最近算出的两个斐波那契数即可，可以推到出O(N)算法。

4.关键代码

递归求斐波那契数列第N个数：

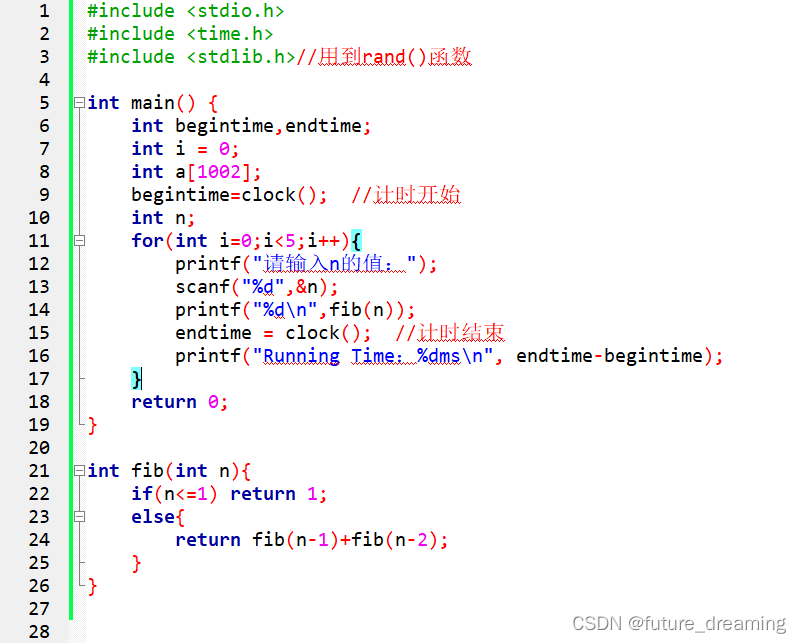
非递归求斐波那契数列第N个数：

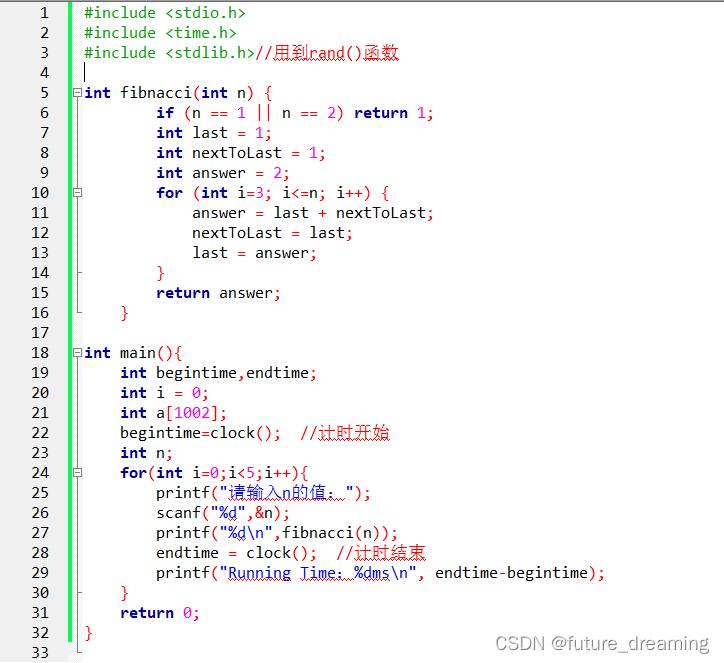
5.运行结果

递归：

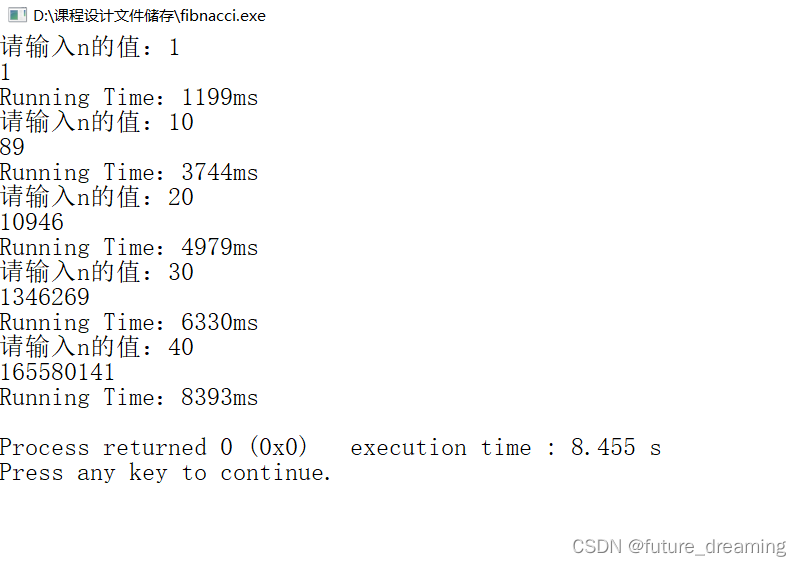
非递归：

方法    N	1	10	20	30	40
递归	1199ms	3744ms	4979ms	6330ms	8393ms
非递归	1121ms	2526ms	3836ms	4962ms	6233ms

                                                    

6.实验总结（含心得体会）

递归算法解决斐波那契数列问题要比非递归算法解决斐波那契数列问题花费更多的时间，当n值越大时越明显。可以通过优化递归算法减少重复计算的次数提高递归算法的效率。