[LeetCode] 460、LFU缓存

题目描述

请你为 最不经常使用（LFU）缓存算法设计并实现数据结构。它应该支持以下操作：get 和 put。

// 在此问题中，当存在平局（即两个或更多个键具有相同使用频率）时，应该去除 最近 最少使用的键。
LFUCache cache = new LFUCache( 2 /* capacity (缓存容量) */ );

cache.put(1, 1);
cache.put(2, 2);
cache.get(1);       // 返回 1
cache.put(3, 3);    // 去除 key 2
cache.get(2);       // 返回 -1 (未找到key 2)
cache.get(3);       // 返回 3
cache.put(4, 4);    // 去除 key 1
cache.get(1);       // 返回 -1 (未找到 key 1)
cache.get(3);       // 返回 3
cache.get(4);       // 返回 4

**进阶：**你是否可以在 O(1) 时间复杂度内执行两项操作？

解题思路

本题其实就是在第146题：LRU缓存机制（先做！）的基础上，在删除策略里多考虑了一个维度（「访问次数」）的信息（LRU就是喜新厌旧，淘汰在缓存里呆的时间最久的元素。在删除元素的时候，只看「时间」这一个维度）。本题的核心思想：先考虑访问次数，在访问次数相同的情况下，再考虑缓存的时间。

• 哈希表 + 双向链表（推荐简要阅读）：

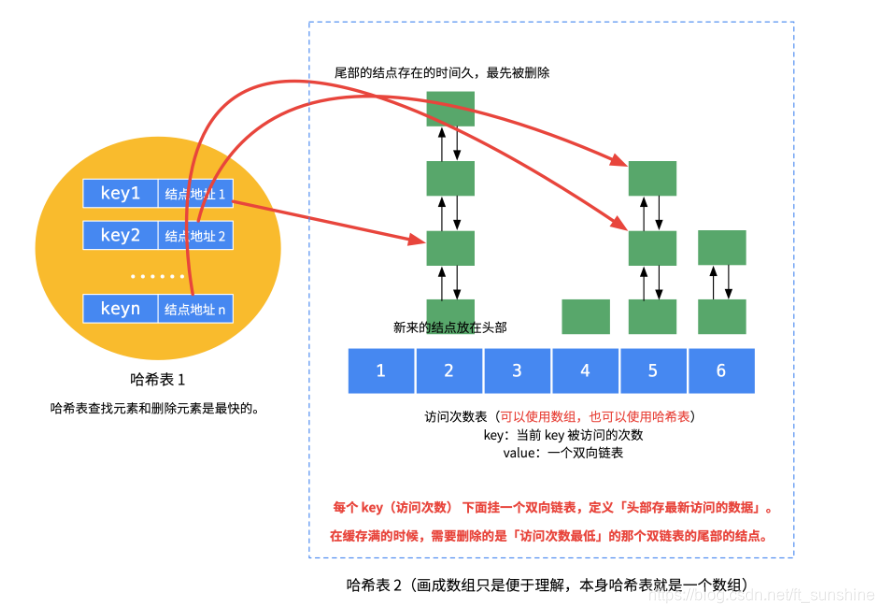
  • 由于题目的时间复杂度要求 $O(1)$，空间肯定不能省，存取数据时间性能最好的就是哈希表，因此底层的数据结构一定是一个哈希表；
  • 又由于缓存大小有限制，删除策略是**「先看访问频次，再看访问时间」**，所以需要记录每个数据已经访问的频次。
  • 「删除某个数据」得 $O(1)$，访问某个数据，时间优先级得提前（提前到当前频次的时间优先级最高处），这样的数据结构符合在头尾访问数据最快，并且删除其中一个结点也得是 $O(1)$，这种数据结构是「双向链表」；
  • 「链表」结点得记录：1、key（在哈希表里删除的时候用得上），2、value，3、访问次数信息freq，以便知道下一个访问次数是多少；
  • 哈希表存储的 key 就是题目的 key，方便快速查询和删除，value 是自定义Node的“迭代器”，方便对结点进行操作。
  • 每次访问一个已经存在的元素的时候：应该先把结点类从当前所属的访问次数双链表里删除，然后再添加到它「下一个访问次数」的双向链表的头部。（双链表的头部看做当前频次链表中时间优先级最高的地方）

  内存结构示意图如下：
  

参考代码

// 缓存的节点信息
struct Node {
    int key, val, freq;
    Node(int _key, int _val, int _freq): key(_key), val(_val), freq(_freq){}
};

class LFUCache {
private:
    int minfreq;  // 当前所有Node的最小使用频率（重要！）
    int capacity;
    unordered_map<int, list<Node>::iterator> umap;
    unordered_map<int, list<Node> > freq_list;
    
public:
    LFUCache(int _capacity) {
        minfreq = 0;
        capacity = _capacity;
        umap.clear();
        freq_list.clear();
    }
    
    int get(int key) {
        if (capacity == 0) 
            return -1;
        auto iter = umap.find(key);
        if (iter == umap.end()) 
            return -1;
            
        list<Node>::iterator node = iter->second;
        int val = node->val;
        int freq = node->freq;
        
        freq_list[freq].erase(node);
        // 如果当前链表为空，我们需要在哈希表中删除，且更新minFreq
        if (freq_list[freq].size() == 0) {
            freq_list.erase(freq);
            if (minfreq == freq) 
                minfreq += 1;
        }
        // 插入到 freq + 1 中
        freq_list[freq + 1].push_front(Node(key, val, freq + 1));
        umap[key] = freq_list[freq + 1].begin();
        
        return val;
    }
    
    void put(int key, int value) {
        if (capacity == 0) 
            return;
        
        auto iter = umap.find(key);
        if (iter == umap.end()) {
            // 缓存已满，需要进行删除操作
            if (umap.size() == capacity) {
                // 通过 minFreq 拿到 freq_list[minFreq] 链表的末尾节点
                Node iter2 = freq_list[minfreq].back();
                freq_list[minfreq].pop_back();
                umap.erase(iter2.key);
                if (freq_list[minfreq].size() == 0) {
                    freq_list.erase(minfreq);
//                    if (minfreq == freq)  // 这里加这个if其实没用，因为这种情况下minfreq最后都要被置为 1
//                        minfreq += 1;
                }
            } 
            
            freq_list[1].push_front(Node(key, value, 1));
            umap[key] = freq_list[1].begin();
            minfreq = 1;  // 当前所有Node的最小使用频率为 1
        } else {
            // 与 get 操作基本一致，除了需要更新缓存的值
            list<Node>::iterator node = iter->second;
            int freq = node->freq;
            freq_list[freq].erase(node);
            if (freq_list[freq].size() == 0) {
                freq_list.erase(freq);
                if (minfreq == freq) 
                    minfreq += 1;
            }
            
            freq_list[freq + 1].push_front(Node(key, value, freq + 1));
            umap[key] = freq_list[freq + 1].begin();
        }
    }
    
};