[LeetCode] 494、目标和

题目描述

给定一个非负整数数组，a1, a2, …, an, 和一个目标数，S。现在你有两个符号 + 和 -。对于数组中的任意一个整数，你都可以从 + 或 -中选择一个符号添加在前面。返回可以使最终数组和为目标数 S 的所有添加符号的方法数。

示例：

输入: nums: [1, 1, 1, 1, 1], S: 3
输出: 5
解释: 

-1+1+1+1+1 = 3
+1-1+1+1+1 = 3
+1+1-1+1+1 = 3
+1+1+1-1+1 = 3
+1+1+1+1-1 = 3

一共有5种方法让最终目标和为3。

解题思路

第一反应这是一个dfs的题目，看了题解后发现这个题竟然可以转换成“背包问题”，OMG。。。

• dfs：代码简洁（我的实现，借助本题，好好体会一下dfs的写法）

  • 时间复杂度：$O(2^n)$
  • 直接dfs时间复杂度略高，可以用“记忆化搜索”来加速（带备忘录memo） —— 用在这里其实不太好，了解即可。

• 动态规划：（转换为01背包问题，相似题目：[LeetCode] 416、分割等和子集）

  • 弄懂题意：第一步需要根据题意考虑输出的结构，在 [LeetCode] 416、分割等和子集 这道题中，要求的输出结果就是bool值，因此我们定义的dp数组只需要记录T/F即可，但是这道题要求返回结果是方法数，那么我们dp数组需要记录的数据就是具体的方法数。

  • 状态定义：搞清楚需要输出的结果后，就可以来想办法画一个表格，也就是定义dp数组的含义。根据背包问题的经验，可以将dp[i][j]定义为对数组nums中 0 - i 的元素进行加减可以得到 j 的方法数量。

  • 状态转移方程：搞清楚状态以后，我们就可以根据状态去考虑如何根据子问题的解，然后转移得到整体的解。这道题的关键不是nums[i]的选与不选，而是nums[i]是加还是减，那么我们就可以将方程定义为：dp[i][j] = dp[i-1][j-nums[i]] + dp[i-1][j+nums[i]]。

    可以理解为nums[i]这个元素我可以执行加，还可以执行减，那么我dp[i][j]的结果值就是加/减之后对应位置的和。

  • 打表格：这个动态规划题“画表格”时与普通的动态规划题有点小不同。我们的表格不能只画每个元素执行加法的情况，而忽略了执行减法的起情况，整个表格区域应该是分为三部分：-/0/+。那么对应的表格的每一行的长度t就可以表示为：t=(sum*2)+1，其中一个sum表示nums中的元素全部执行+/-所能达到的数，具体表格如下图所示：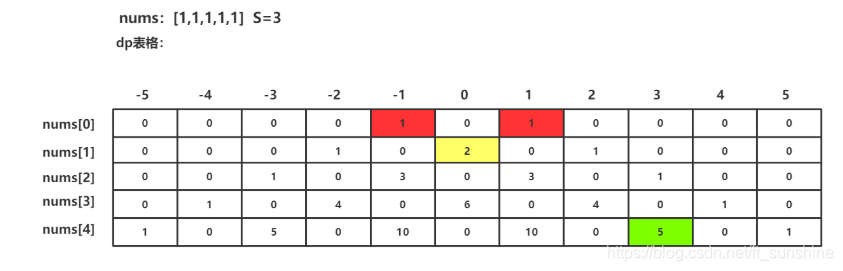

    

  • 初始化：根据“状态转移方程”，我们需要初始化表格的第一行。

    这道题有个坑的地方，就是nums[0]可能等于0，这样初始化dp数组第一行的时候很可能踩坑，因为如果nums[0]==0，那么dp[0][sum]需要初始化为2，因为加减0都得0。

  • 返回值：绿色部分的表格值就是我们本题的解：dp[len-1][sum+s]。

参考代码

dfs

class Solution {
public:
    int findTargetSumWays(vector<int>& nums, int target) {
        int length = nums.size();
        if(length == 0)
            return 0;

        int res = 0;
        dfs(nums, 0, 0, target, res);

        return res;
    }

    void dfs(vector<int>& nums, int curIndex, int curSum, int target, int &res){
        if(curIndex == nums.size()){
            if(curSum == target)
                res++;
            return;
        }
        
        // 此处dfs只有两种可能/选择：+/-， 所以这里不用再写for循环，直接列举所有选择即可。
        // cf：《剑指offer》 p296
        dfs(nums, curIndex + 1, curSum + nums[curIndex], target, res);
        dfs(nums, curIndex + 1, curSum - nums[curIndex], target, res);
        
//        // 错误写法！！！！！
//        // for循环没有任何意义，之前不太会的时候瞎写的，做多题之后，现在我也看不懂啥意思了，完全在胡写
//	   	  // 因为本题在每个位置处必须有操作：+/-，而for循环的每一次迭代都会跳过当前的位置（在当前位置不做操作）
//        for(int i = curIndex; i < nums.size(); i++){    // 这里不应该再加循环
//            dfs(nums, i + 1, curSum + nums[i], target, res);
//            dfs(nums, i + 1, curSum - nums[i], target, res);
//        }
    }

};

动态规划

class Solution {
public:
    int findTargetSumWays(vector<int>& nums, int target) {
        int length = nums.size();
        int sum = accumulate(nums.begin(), nums.end(), 0);
        // target的绝对值范围超过了sum的绝对值范围则无法得到
        if(abs(target) > abs(sum))
            return 0;
        
        // - 0 +
        int t = 2 * sum + 1;
        vector<vector<int> > dp(length, vector<int>(t, 0));
        
        // 初始化
        if(nums[0] == 0){
            dp[0][sum] = 2;  // 特判
        }else{
            dp[0][sum-nums[0]] = 1;
            dp[0][sum+nums[0]] = 1;
        }
        
        for(int i = 1; i < length; i++){
            for(int j = 0; j < t; j++){
                int left = (j - nums[i] >= 0 && j - nums[i] < t)? dp[i-1][j-nums[i]]: 0;
                int right = (j + nums[i] >= 0 && j + nums[i] < t)? dp[i-1][j+nums[i]]: 0;
                dp[i][j] = left + right;
            }
        }
    
        return dp[length-1][sum+target];
    }

};