马尔科夫链原理介绍【通俗易懂】

介绍

马尔科夫链是一种非常常见且相对简单的统计随机过程，从文本生成到金融建模，它们在许多不同领域都得到了应用。马尔科夫链在概念上非常直观且易于实现，因为它们不需要使用任何高级的数学概念，是一种概率建模和数据分析的经典方法。

1. 马尔科夫链场景分析

首先，我将用一个非常常见的例子来描述它们：

假设有两种可能的天气状态：晴天或阴天，你随时都可以观测当前的天气状态且状态限定为晴天或阴天。

现在你想预测明天的天气情况，你本能的会认为当天的天气会对明天的天气有一定的影响，因此，拥有智慧和才貌的你会收集并分析过去几年的天气数据，发现了一个规律——当天是阴天第二天是晴天的概率为0.25，由于天气限定为晴天或阴天，那么当天是阴天第二天也是阴天的概率为0.75。

因此你可以基于当前的天气状态去预测未来几天的天气。

这一例子阐述了马尔科夫链的关键概念：马尔科夫链本质上是由满足马尔科夫性质的转移概率分布组成，下图为天气例子的转移概率：

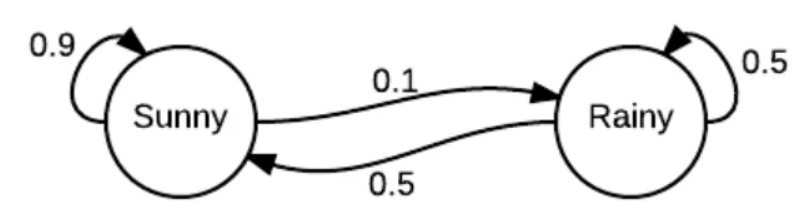
马尔科夫的性质在于它的无记忆性，下一时刻的状态只与当前的状态相关。用数学公式描述为：

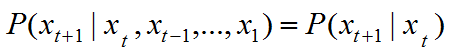
其中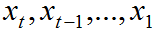是时间状态序列。

这个例子介绍了如何仅通过观察当天到下一天的转移来获得概率分布，这说明了马尔科夫的性质在于它的无记忆性。

马尔科夫的无记忆性通常使它们无法成功预测某些潜在会发生的趋势，比如马尔科夫链可能根