Matlab答疑五：使用微分定义求解微分方程的数值解

1.题目

解微分方程 dydt=sin(y)+t，其中t=0时y=0，并绘图。

说明，一般对dydt的求解方法为：y(t+dt)=y(t)+dydt(t)*dt

2.方法

除了题目给出方法：使用定义求解；还可以使用dsolve符号运算，以及使用ode45的数值解法；下面使用三种方法求解，并对比结果。

3.程序

%1 按照题目思路编程求解，程序如下：

dydt=@(t,y)sin(y)+t;

dt=0.001;

t=0:dt:10;

y=0;

for i=1:length(t)

    y(i+1)=y(i)+dydt(t(i),y(i))*dt;

end

y(end)=[];

plot(t,y),grid on

% 2 使用dsolve求解析解（无解），程序如下：

% syms y(x)

% ode=diff(y,x)-sin(y)==x;

% cond=y(0)==0;

% dsolve(ode,cond)

警告: Unable to find symbolic

solution.

> 位置：dsolve (第 209 行)

位置: freexyn67 (第 8 行)

 ans =

 [ empty sym ]

%3 使用ode45数值解法，程序如下：

tspan=[0 10];

y0=0;

opts=odeset('reltol',1e-2,'abstol',1e-4);

[x,y]=ode45(@ode,tspan,y0,opts);

plot(x,y),grid on

function dy=ode(x,y)

dy=sin(y)+x;

end

4.结果

使用dsolve求解无解，另外两种方法获得结果一致，图像如下所示：

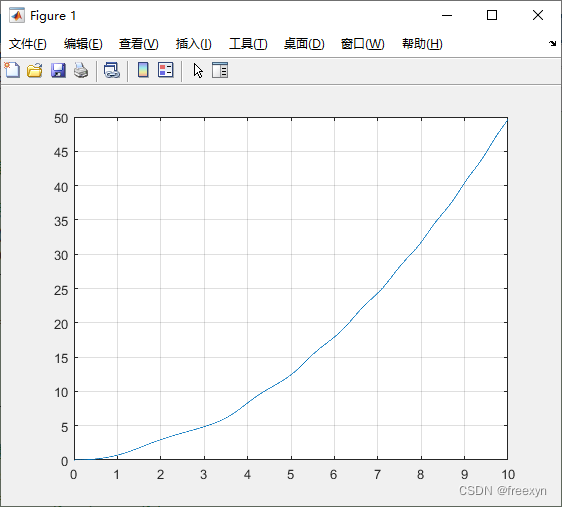
使用微分定义求解的图像

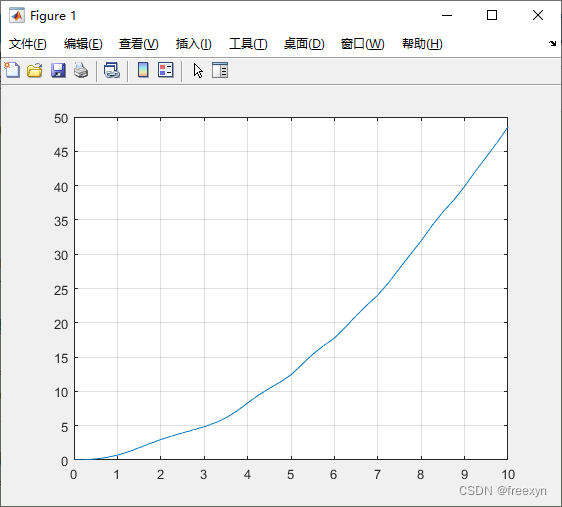
使用ode45求解的图像

更多内容请关注我们，统一昵称：freexyn

End