CS61B - Lec33 - Quicksort

这一章学习了运用广泛的quicksort，其中运用了分治的思想。

Backstory, Partitioning

Quicksort是在1960年，Tony Hoare在解决一个翻译问题时发明。

有这样一句话：“The cat wore a beautiful hat."，任务是将它翻译成俄文。现有一个俄文英文对照的dictionary，直接将每个单词对应的俄文组合起来就行了，是一种简陋的翻译方法。按照现在的技术，自然会想到dictionary是个HashMap，或者用二分法查找每个单词。
然而，那时访问数组元素并不是常数时间。dictionary是存储在一个长长的tape上，每次找一个元素只能从开头依次访问到它的位置，所以HashMap和二分法效率也很低。
所以，聪明的大佬想到了先把句子排一下序，然后从头到尾遍历一遍字典就可以了。下面的问题就是如何给这个句子排序呢？

然后他就发明了quicksort。

Quicksort

Quicksort的算法其实很简单：

• Partitioin最左边的数
• Quicksort左边一半
• Quicksort右边一半

其中partition的意思就是，将该数移动到一个位置，是的它的左边所有数小于等于它，右边所有数大于等于它。（此时该数称之为pivot)

思路很简单，但是有两个关键问题要解决：

1. 如何partition?
2. 怎么证明quicksort很"quick"?

Quicksort Runtime

先不谈partition的问题，分析一下runtime。

首先partition操作的runtime是O(K)，K为partition的数量。

理想情况下，每次pivot都正好在中间位置，每一层partition * 分块数 = N，共有log(N)层，所以runtime为O(Nlog N)。

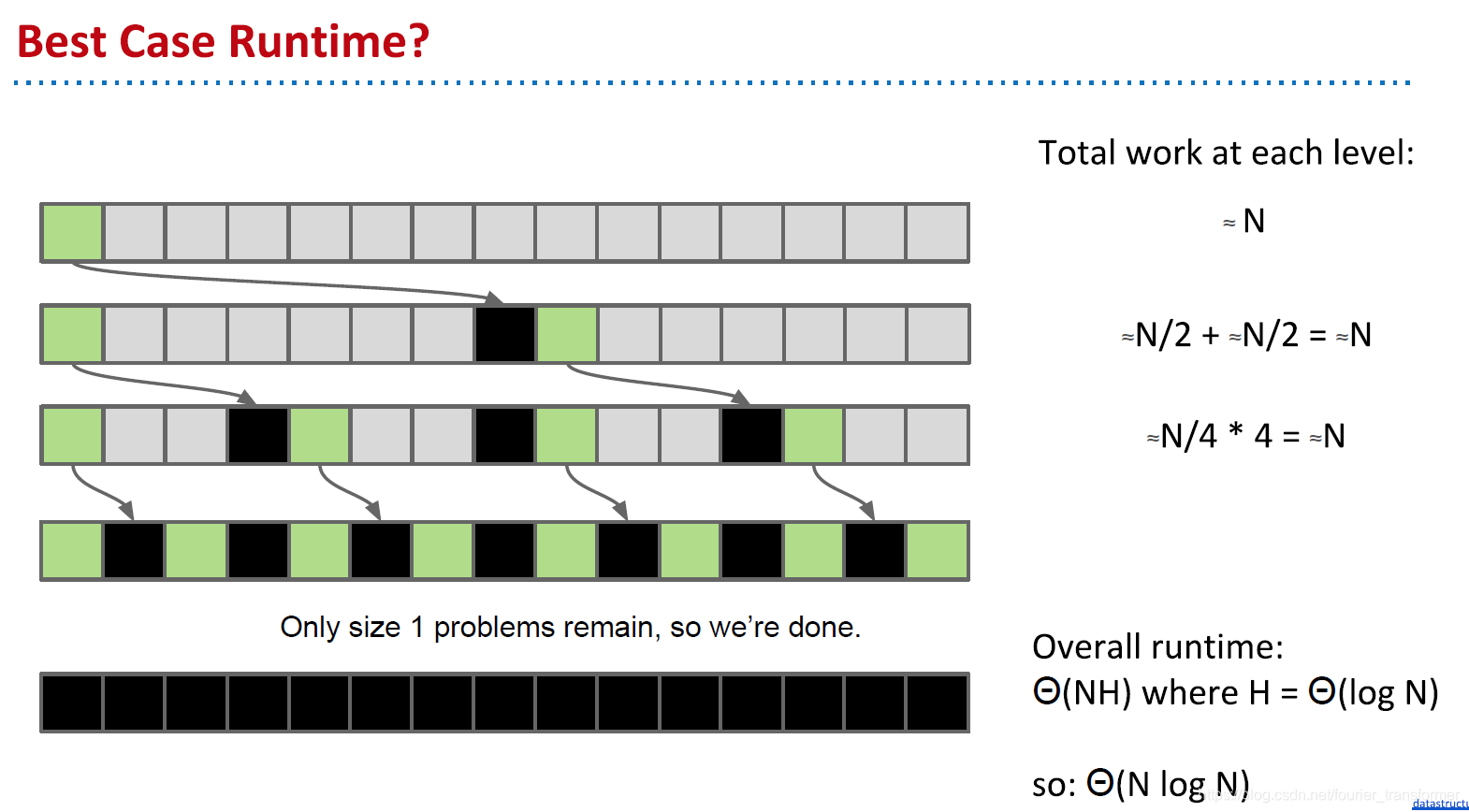
最坏情况下，pivot一直在开头，每层同样的partition操作，但是层数变成了N，所以最后runtime为O(N²）。

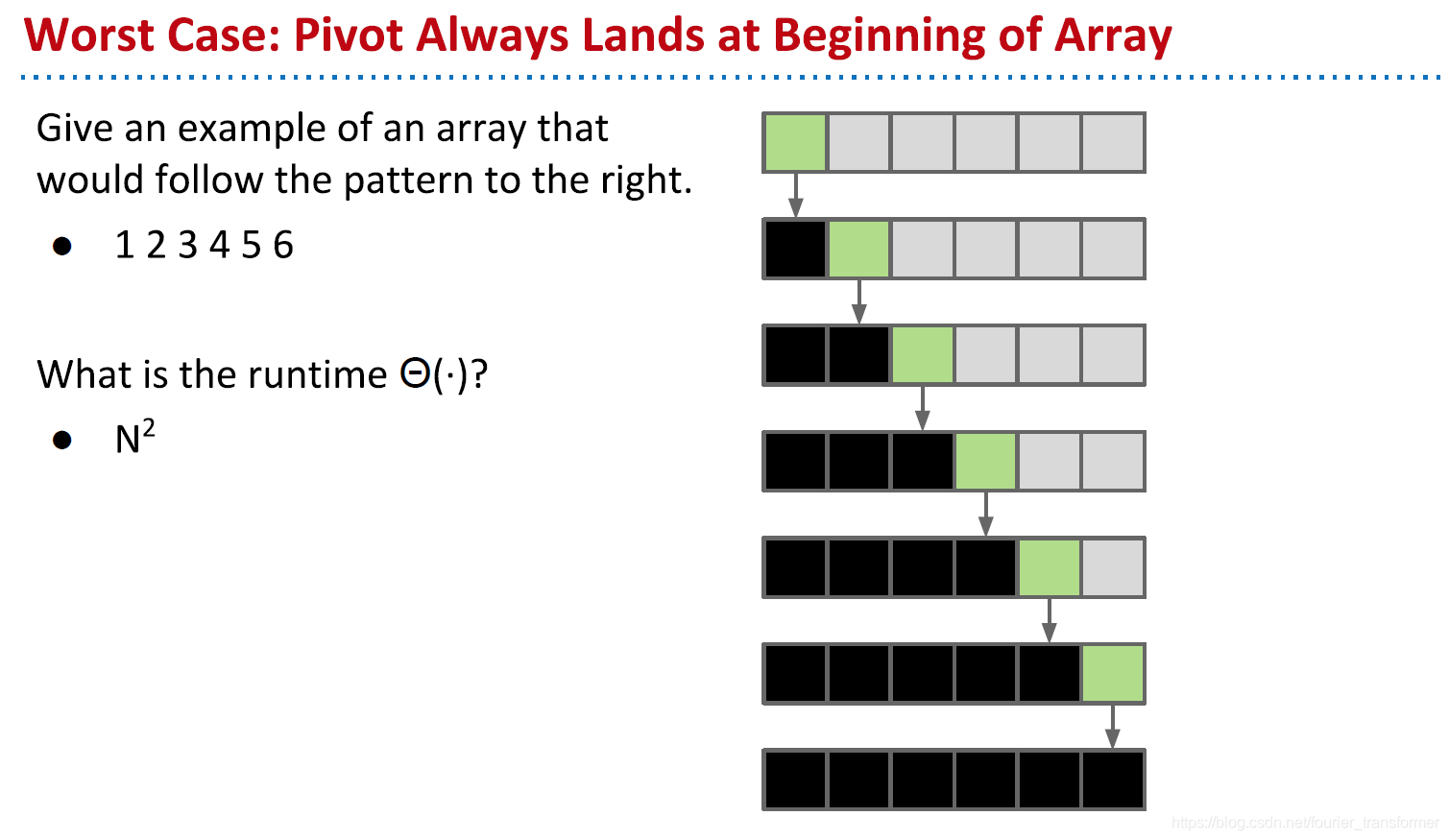
这并没有多优秀啊，merge sort一直就是O(Nlog N)。

简要分析一下。即便是一种极端倾斜的情况，pivot一直处在左10%的位置，层数依然是和logN相关的log_10/9N，复杂度依然是O(Nlog N)。

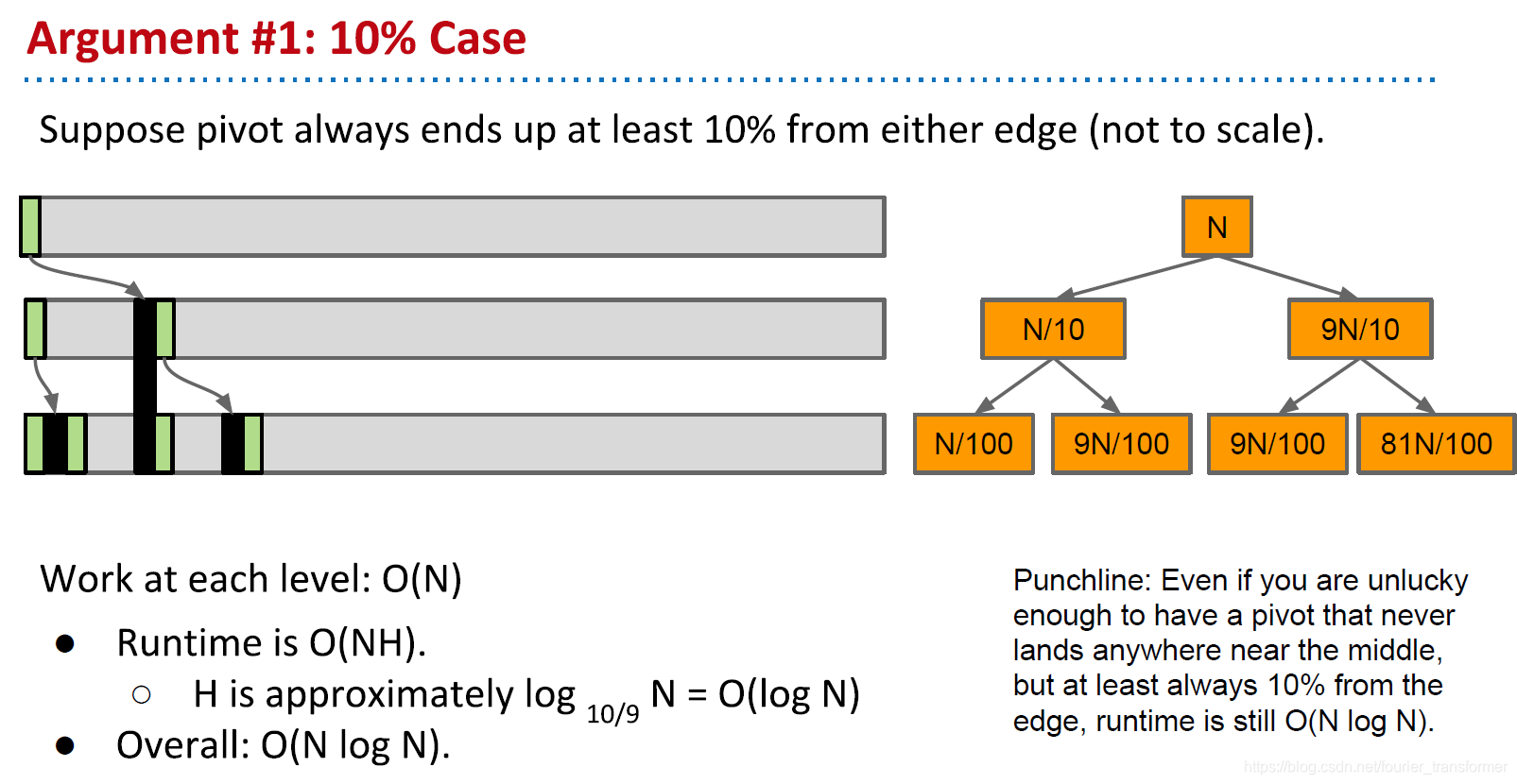
另一方面，可以看出quicsort和BST是有一定联系的。

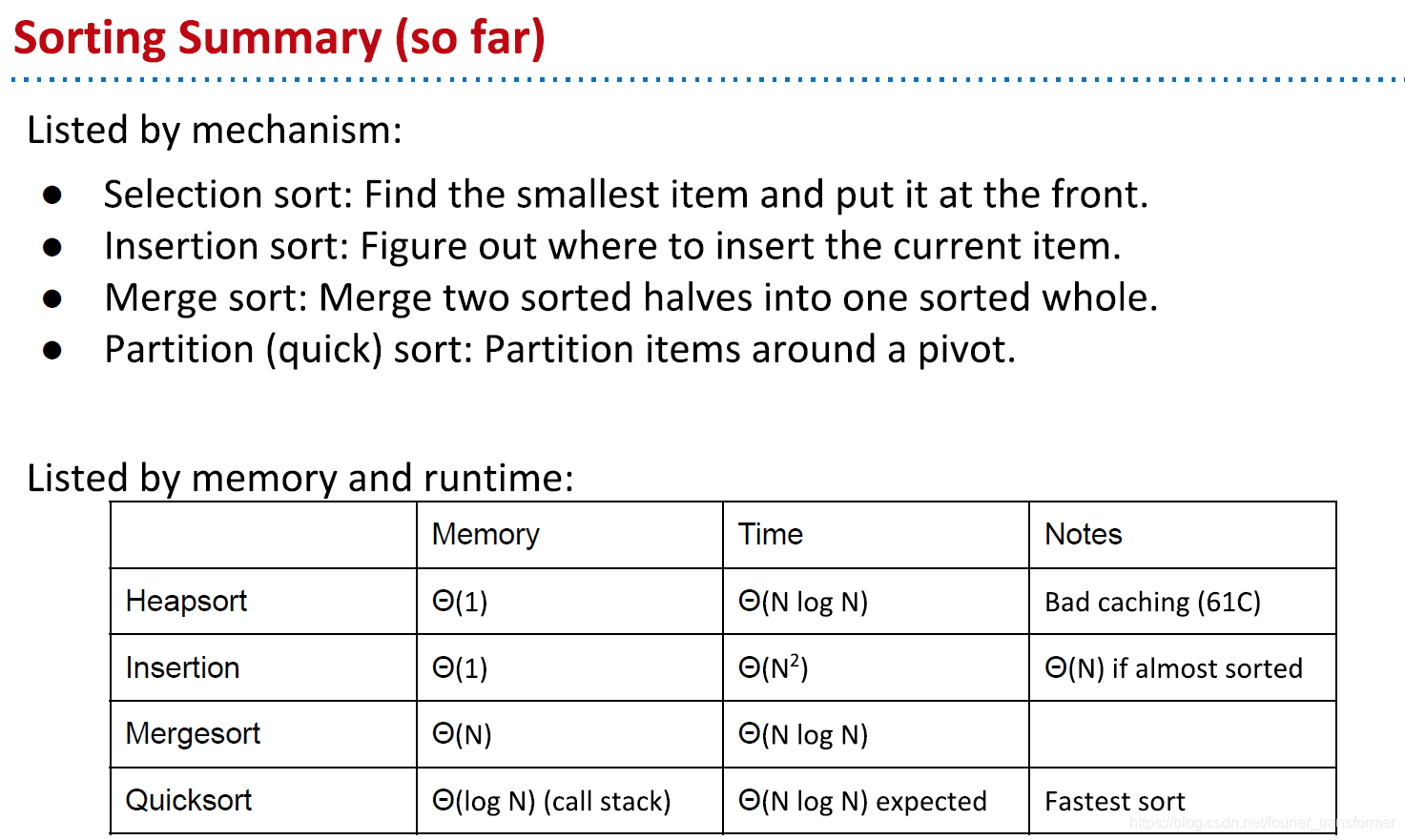
所以其实在大部分情况下，quicksort还是O(N logN)，但是为什么它就比mergesort快呢，课上没给出答案。

Avoid the Quicksort Worst Case

我觉得可以随机选择pivot而不是从最左边。下次课会继续讲quicksort。