CS61B - Lec 32 - Basic Sort

今天正式进入phase 3，算法阶段。

Sorting Problem

今天只是个基础所以内容还是很愉快的。排序算法是很多算法的基础，并且分析的过程也可以举一反三，所以作为算法篇的开头。这里主要探讨了排序的几种方式以及优化。

Selection Sort and Heapsort

Selection Sort(选择排序)：找到当前位置到结尾最小的数据，和当前位置交换，重复直到结尾。复杂度为O(N²)。发现很没有效率，很多数据被遍历了多遍，信息并没有保存下来。空间复杂度为O(1)。

Native Heapsort: 先用所有的数构建一个heap（max-oriented)。然后从结尾往开头，依次从大到小插入。
构建需要Nlog N，remove+插入也是Nlog N，所以最后复杂度优化为O(Nlog N)。

然而需要一个构建一个heap，额外花费了存储空间。空间复杂度为O(N)，可以通过优化优化到常数。

In-place Heapsort：由于它的完整性，heap可以只用一个数组表示（见heap章），所以完全可以在原数组上构建heap。

首先原数组可以表示成这样一个heap。

然后从尾部开始，一个一个进行sink。sink就是如果发现一个数比他的子节点小，那么就往下沉，直到满足heap定义。

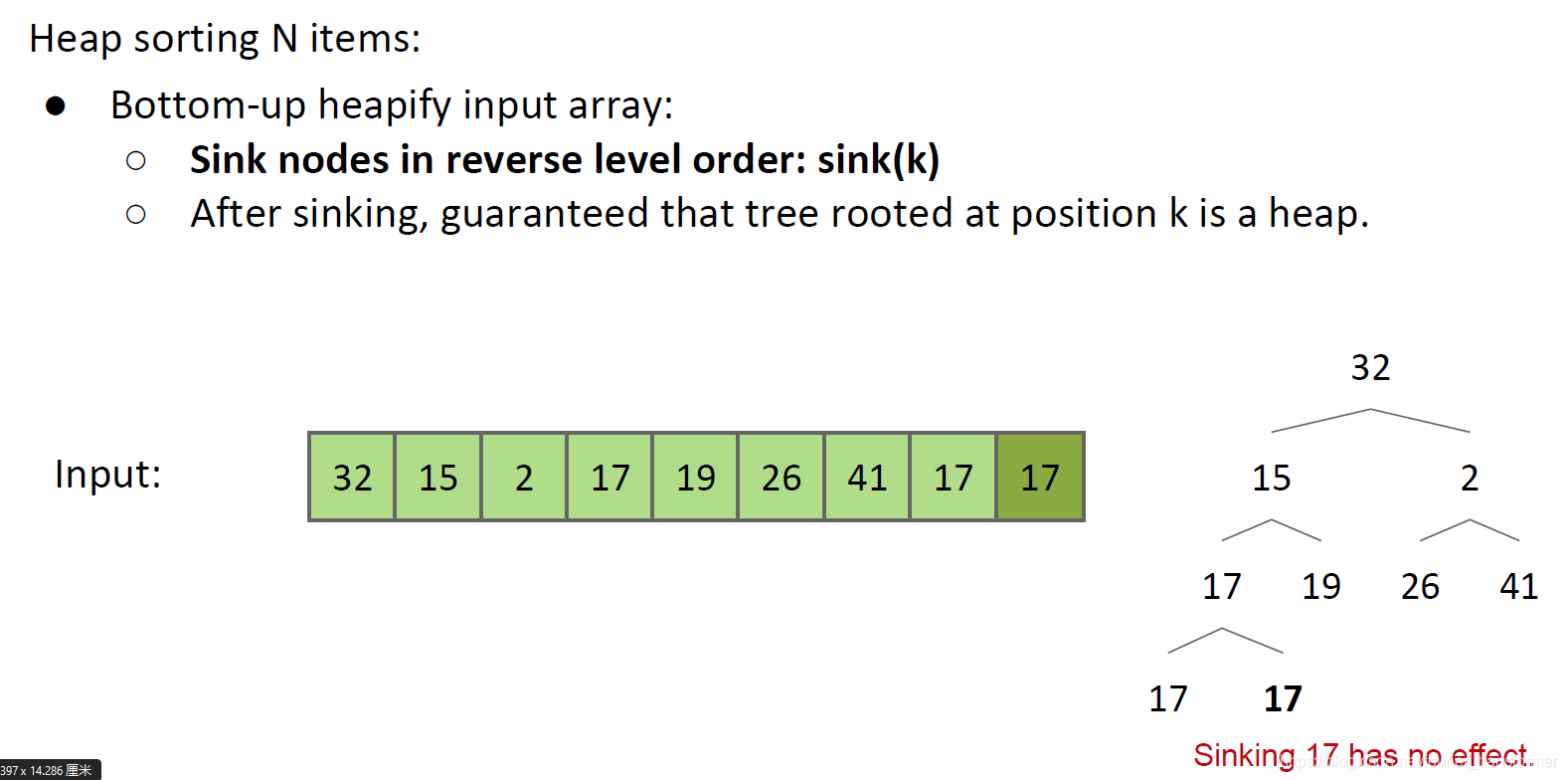
直到17，sink都没有作用。

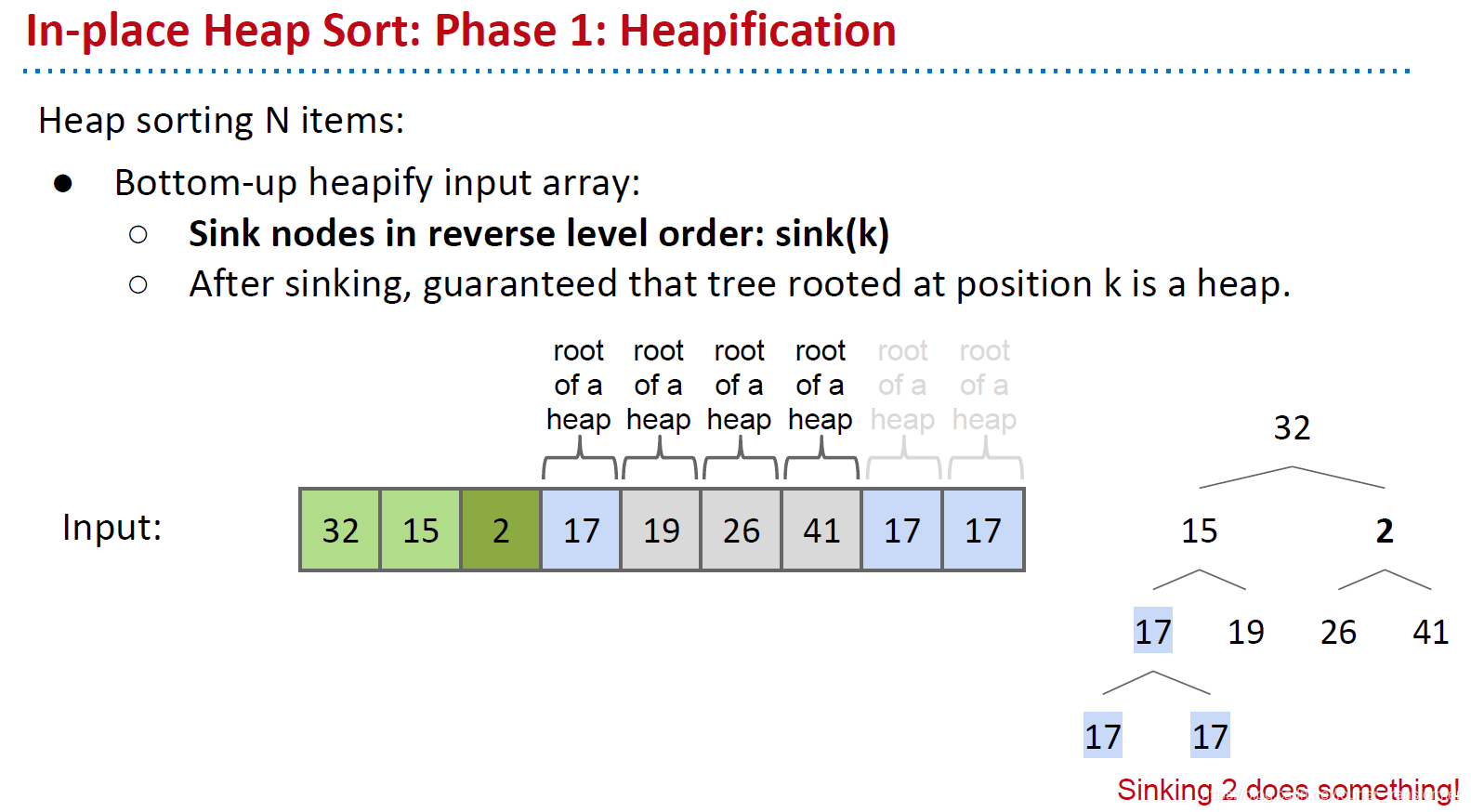
到2的时候，发现2比子节点26和41都要小，所以将2和41交换。

15同理，和19交换。

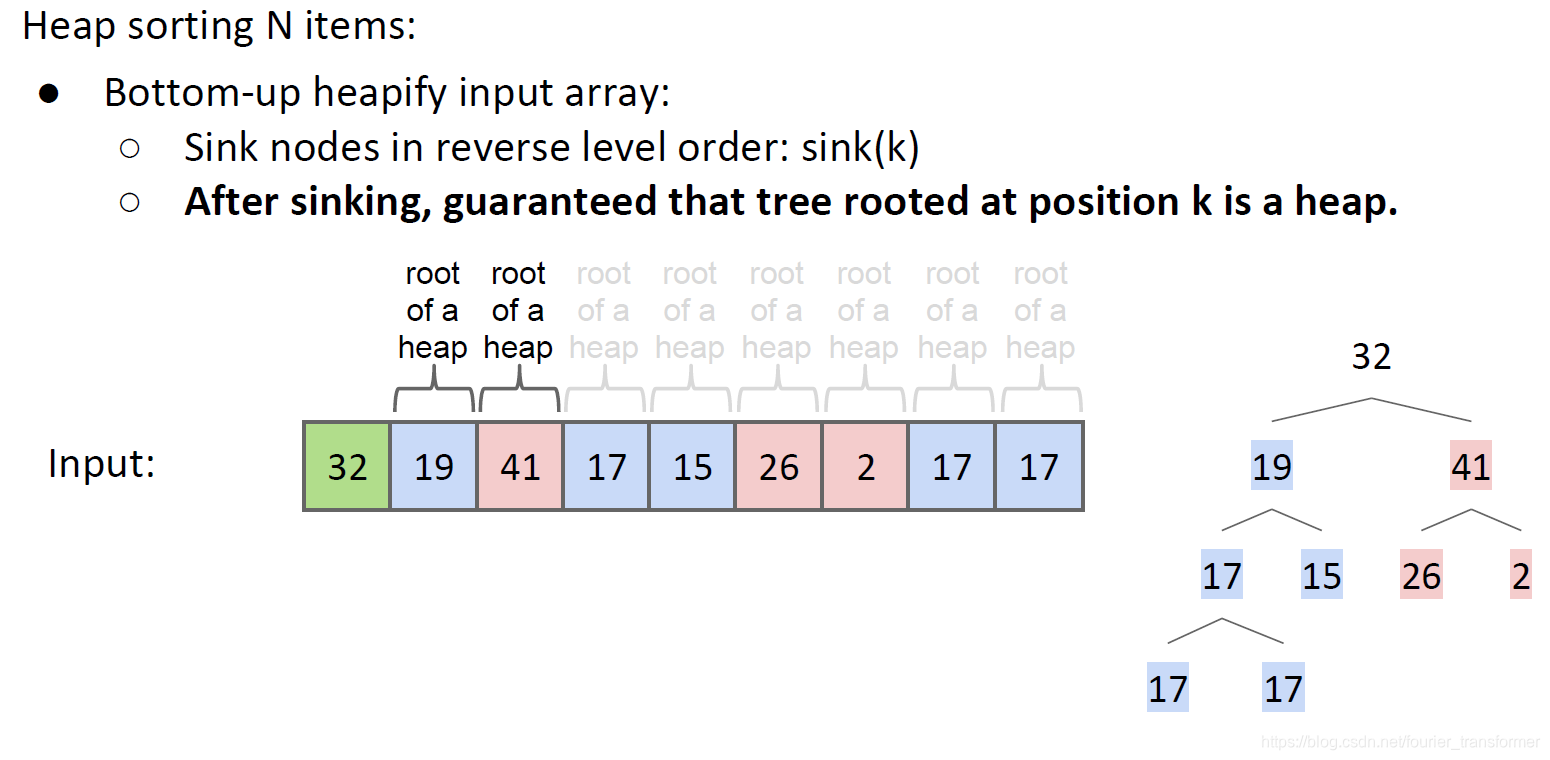
最后，32和41交换。从尾部开始sink的意义是：保证以该位置作为root的树是一个heap，也就是该位置之后全部满足heap的条件。这是我们就有了一个max-oriented heap。

对这个heap进行这样的操作：删除最大的。（把最大的数和heap末尾交换，并且交换末尾的数直到满足heap的定义）。直到heap为空。


时间复杂度依然是O(Nlog N)，但空间复杂度优化为O(1)。

Mergesort

早在复杂度分析的第二章就接触到了mergesort。它的时间复杂度为O(Nlog N)，空间复杂度为O(N)。josh说in-place的mergesort非常难，他也不会。

Insertion Sort

插入排序，一般的思路是这样：首先建一个空数组，然后遍历原数组，依次将每个数字插入到新建数组的正确的位置。

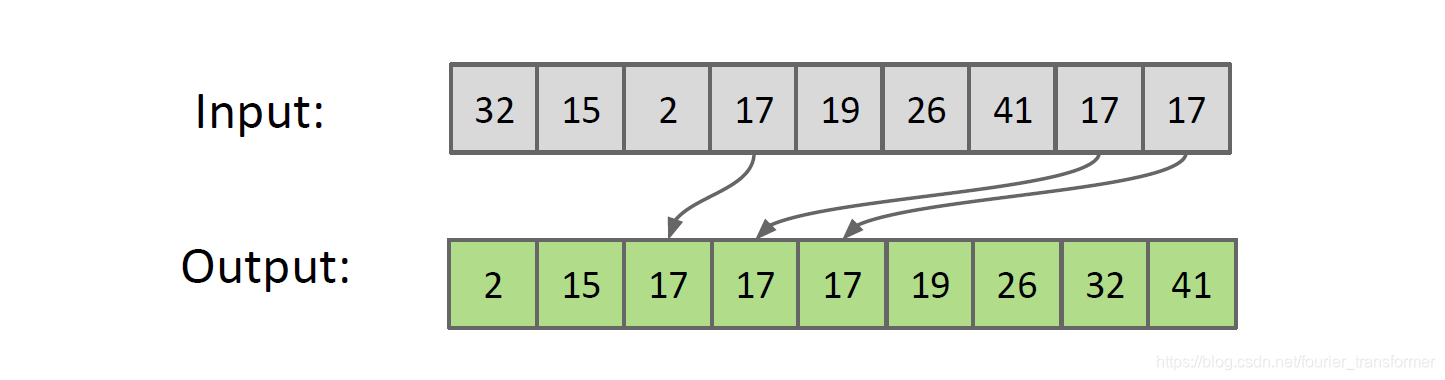
需要额外的存储空间，并且对于数组，插入会不断地移动位置，可以优化成in-place。
依然需要遍历整个数组，但是可以通过swap的方式换到正确的位置。如下图，指针i代表当前遍历的数据，j记录下每次交换的位置。

i, j都在开头，没有要交换的，换到下一项。

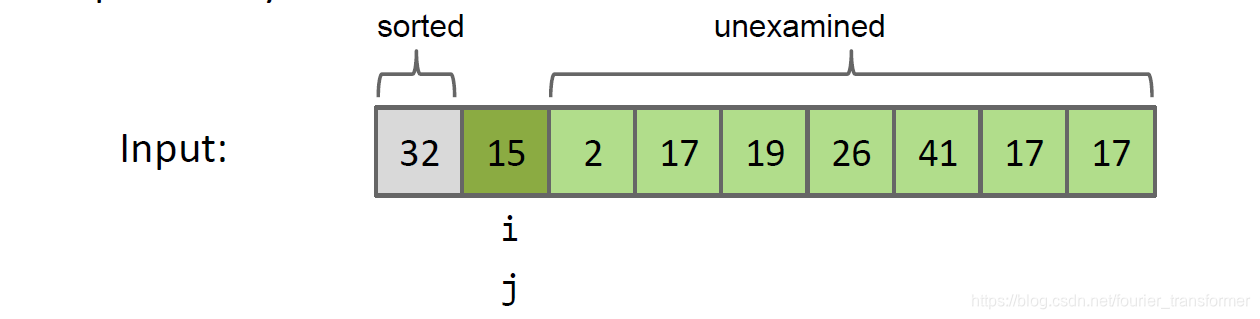
15和32比较，交换15和32，j记录下15交换的位置。

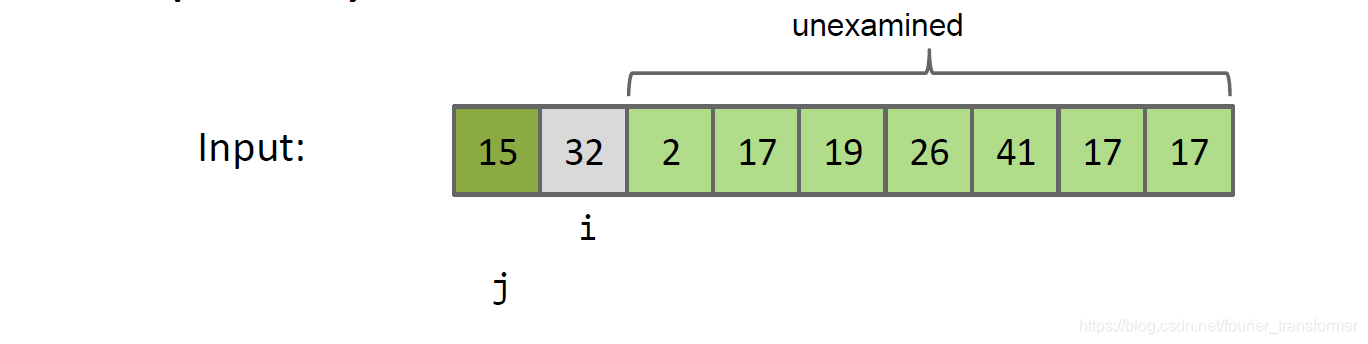
交换完毕，i，j到下一项。

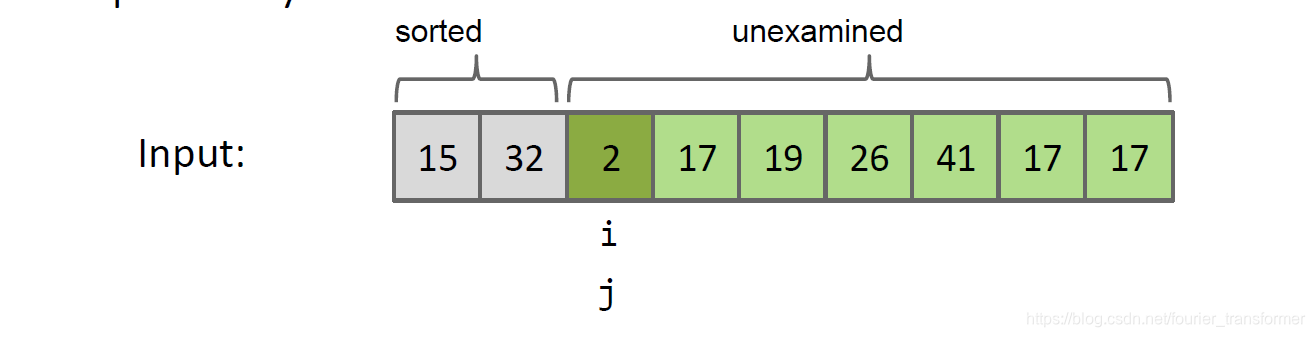
2<32，交换。

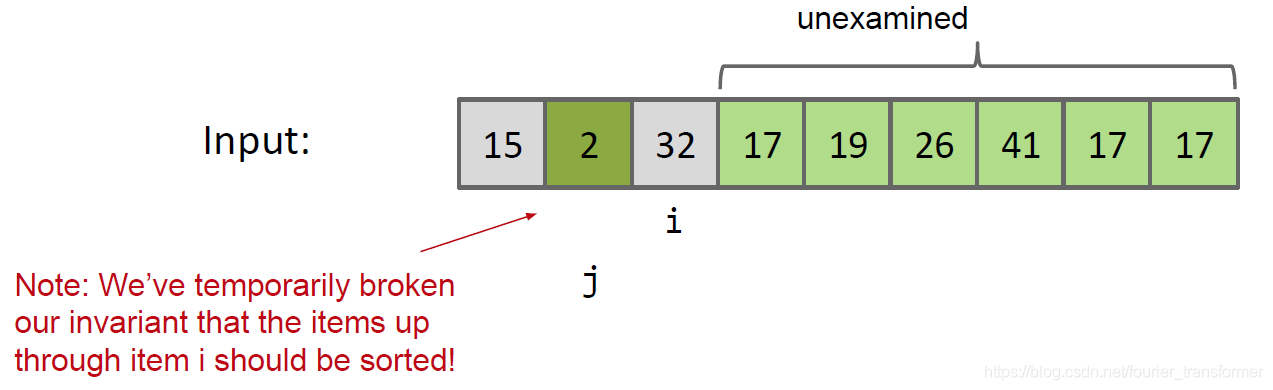
2<15，交换，2，25，32排序完毕。剩下的思路相同。

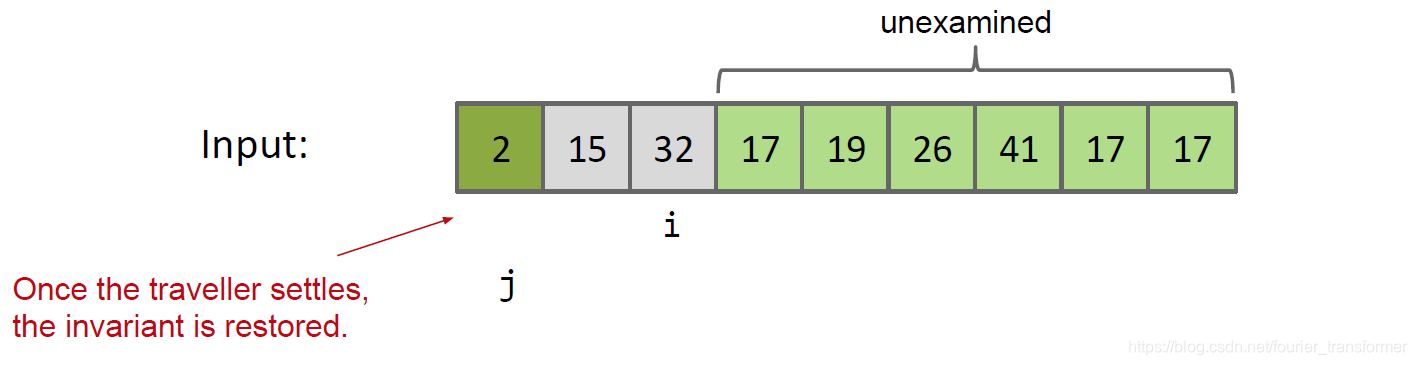
分析runtime，最好情况下，只需要遍历一遍整个数组，这时为O(N)；最坏情况下，也就是从大到小排列时，跟冒泡一样了，为O(N²)。

貌似Insert Sort没有什么优越之处，然而看以下的问题：先搞1000000个排序好的整数，然后改变一个，重新排序，这时选用什么排序算法效率高呢？

这时，用insertion sort排序比较好。因为只需遍历一遍，再加上常数次的swap，就可以实现排序。Selection sort不用说，依然需要O(N²)；Heap Sort还是需要重新建立heap，依然需要O(Nlog N)；Insertion Sort却只需要O(N)了。

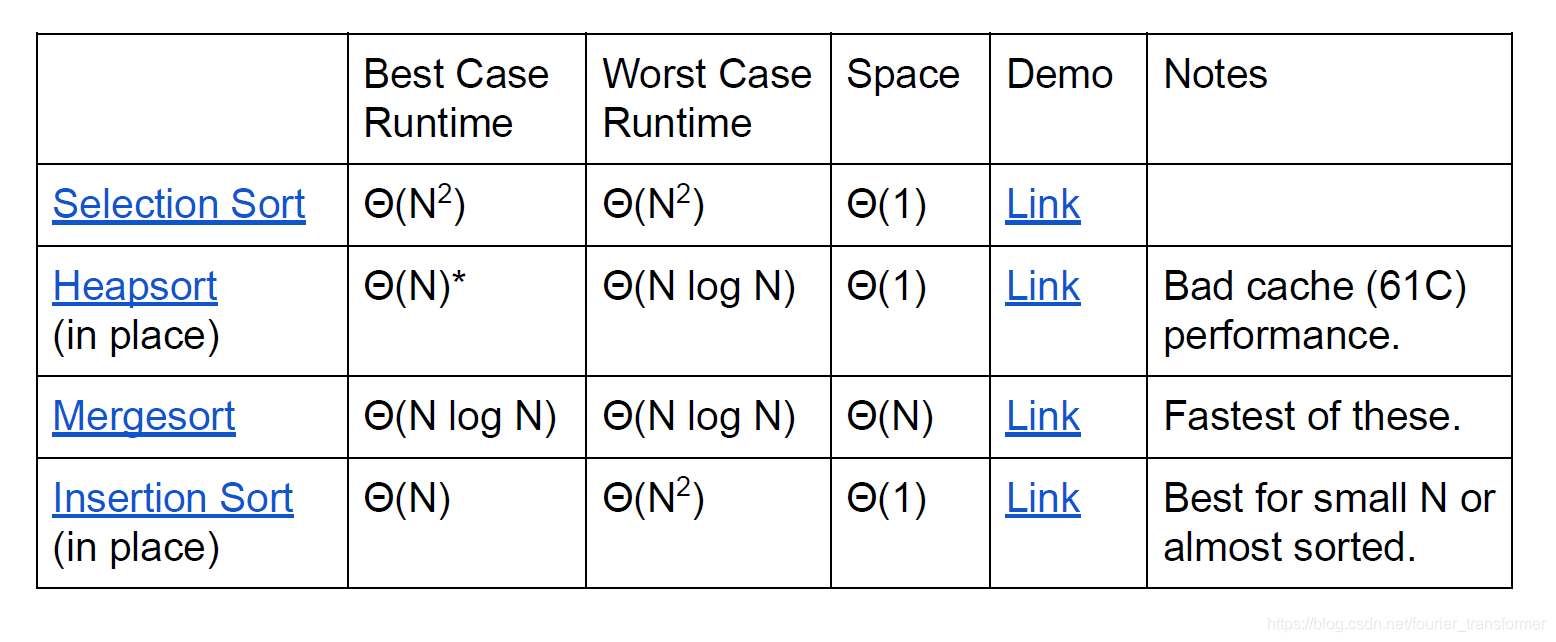
经研究表明，Insertion sort对于小数组和almost sorted的数组，性能最佳。

几种算法各有千秋。这跟ADT是一样的，不同的地方用不同的算法/数据结构。