随机森林算法原理简要总结

①Random Forest 随机森林算法原理：
即bagging法+CART算法生成决策树的结合。

R F = bagging + fully-grown CART decision tree

②bagging法的核心：bootstrap在原始数据集D中选择若干个子数据集Dt，将子数据集单个单个进行决策树生成。

③随机森林的优点：

• 可并行化计算（子集的训练相互独立），效率高
• 继承了CART算法的优点（使用Gini系数选择最优特征及切分点）
• 减小了完全生成树的弊端（因为完全生成树过于复杂，Ein小但Eout大；如果不与bagging结合的话，决策树的训练是要先生成再剪枝的，而RF当中就不需要剪枝了，因为bagging法使得各个子集的决策树不会过于复杂）

④误差Eoob（out of bag 袋外误差）

此处参考博客：
作者：快乐的小飞熊
链接：https://www.jianshu.com/p/b94ec2fc345d
来源：简书

• 在随机森林bagging法中可以发现booststrap每次约有1/3的样本不会出现在bootstrap所采集的样本集合中，故没有参加决策树的建立，这些数据称为袋外数据oob，用于取代测试集误差估计方法，可用于模型的验证。（优点是不需要另外划分validation验证集，袋外数据直接作为验证数据，在模型训练之时就计算出了误差。即袋外误差）
  下面先介绍下oob的使用，其中（x,y）代表输入的样本和label，g表示的是构建的树。
  
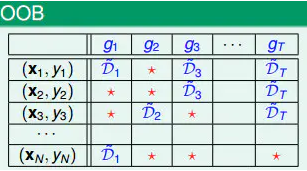
  上图中（xN,yN）没有用于g2、g3、gt，所以（xN,yN）可以作为g2、g3、gt的验证数据，然后此oob数据作为输入，输入到模型中，然后投票，少数服从多数。
  同理，对于（x1,y1)、（x2,y2)等也存在同样的计算，最终计算评判错误的样本占比，就是oob-error.
  所以oob可以用来衡量RF模型的好坏。

• 同时，也可以引出随机森林输出特征重要性的原理：如果特征i对于模型是有利的，那么第i维特征置换成随机值，将会降低模型的性能，也就是会使oob-error变大。
  根据这个原理，我们可以进行特征选取，即去除冗余的、相关性差的特征。（也称为置换试验）
  importance(i) = Eoob(G) - Eoob^p(G)
  其中Eoob^p(G)就是被替换掉第i维特征值后的数据集的Eoob。

---

END