伪谱法求解PDE

伪谱法基本原理

伪谱法适用条件：如果你想在一个简单的领域上高精度地解决一个ODE或PDE，且如果定义问题的数据是平滑的，那么伪谱法通常是最好的工具，伪谱法通常可以达到10位数的精度，其中有限差分或有限元方法将得到2到3位数。在较低的精度下，伪谱法比其他方法需要更少的计算机内存。

在伪谱法中，偏微分方程的解是由一组正交函数 { φ j ( x ) } j = 0 ∞ \{\varphi_j(x)\}_{j=0}^\infty {φj​(x)}j=0∞​的有限线性组合来近似的:
$$\begin{array}{c}{f}_N(x)=\sum _{k=0}^N{\hat{f}}_k{\phi }_k(x)\end{array}$$其中${\hat{f}}_k$被称为$f$相对于基函数 { φ k } \{\varphi_k\} {φk​}的谱系数，${\hat{f}}_k$是$f$在${\phi }_k$“方向”上的度量，可以通过一个积分来计算
$$\begin{array}{c}\begin{array}{r}{\hat{f}}_k=\int f(x){\phi }_k(x)\omega (x)\mathrm{d}x\end{array}\end{array}$$其中，$\omega (x)$是一个与基函数 { φ k } \{\varphi_k\} {φk​}相关联的权重函数。
假设，我们考虑的是在$[0,2\pi ]$内的周期函数，其中一个基函数是由正弦和余弦组成的傅里叶基函数，如 { cos ⁡ k x ， sin ⁡ k x } k = 0 ∞ \{\cos kx，\sin kx\}^∞_{k=0} {coskx，sinkx}k=0∞​，其简洁的复数形式为 { e i k x } k = − ∞ ∞ \{e^{ikx}\}^{\infty}_{k=-\infty} {eikx}k=−∞∞​，如果$f$满足一些条件，如连续性和有界可微，可以证明由$f_N(x)={\sum }_{k=0}^N{\hat{f}}_k{e}^{ikx}$其中${\hat{f}}_k=\int f(x)e^{ikx}\mathrm{d}x$给出的,$f$随着$N$的增加一致收敛于$f$。
$f$的导数近似为$f_N^{{}^{\prime }}$，由下式给出：
$$\begin{array}{c}\begin{array}{r}{f}_N^{{}^{\prime }}(x)=\sum _{k=0}^N{\hat{f}}_k{\phi }_k^{{}^{\prime }}(x)\end{array}\end{array}$$$f_N^{{}^{\prime }}$被称为$f$的伽辽金谱导数。一旦我们知道了导数${\phi }_k^{{}^{\prime }}$（一般的递推公式）的细节，我们就可以计算出公式$(3)$，并找出系数${\hat{f}}_k$来导出$f_N^{{}^{\prime }}(x)={\sum }_{k=0}^N{\hat{f}}_k^{{}^{\prime }}{\phi }_k(x)$。
例如，设$f$是$[0,2\pi ]$中的一个偶数周期函数。近似$f$的一个合适的基函数是傅里叶基函数。如果我们写的话：
$$\begin{array}{c}\begin{array}{r}{f}_N(x)=\sum _{k=0}^N{\hat{f}}_k{e}^{ikx}\end{array}\end{array}$$我们很容易看到，$f$的一阶和二阶导数的近似是：
$$\begin{array}{c}\begin{array}{r}{f}_N^{{}^{\prime }}(x)=\sum _{k=0}^N\left(ik{\hat{f}}_k\right)e^{ikx}\\ f_N^{{}^{\prime \prime }}(x)=\sum _{k=0}^N\left(-k^2{\hat{f}}_k\right)e^{ikx}\end{array}\end{array}$$这就是说，一旦我们知道了谱系数${\hat{f}}_k$，我们就通过将每个${\hat{f}}_k$乘以$-k^2$得到了$f^{{}^{\prime \prime }}$的近似值。例如使用伪谱法，将谱系数分别乘以$ik,(ik{)}^2,(ik{)}^3$来求解函数$f(x)=\sin (\pi (x+1))e^{\cos (\pi (x+1))}$的一次、二次与三次导数的结果如下：

伪谱法求导结果

伪谱法求解声波方程

声波方程为：
$$\begin{array}{c}\begin{array}{r}{\partial }_t^{2}u=v^2{\nabla }^{2}u=v^2({\partial }_x^2+{\partial }_y^2)u\end{array}\end{array}$$将上式对空间的偏导数用伪谱法表示可得：
$$\begin{array}{c}\begin{array}{r}{v}^2({\partial }_x^2+{\partial }_y^2)u=v^2{F}^{-1}\left[-(k_x^2+k_y^2)F(u)\right]\end{array}\end{array}$$其中$F$为傅氏正变换，$F^{-1}$为傅氏逆变换。对时间的偏导数项用二阶中心差分表示为：
$$\begin{array}{c}\begin{array}{r}{\partial }_t^{2}u=\frac{u^{n+1}-2u^n+u^{n-1}}{\Delta t^2}\end{array}\end{array}$$将（1）和（8）式代入到（6）中去，可得：
$$\begin{array}{c}\begin{array}{rl}{\partial }_t^{2}u& =\frac{u^{n+1}-2u^n+u^{n-1}}{\Delta t^2}=v^2{F}^{-1}\left[-(k_x^2+k_y^2)F(u)\right]\\ u^n& =(\Delta t^2{v}^2)F^{-1}\left[-(k_x^2+k_y^2)F(u)\right]+2u^n-u^{n-1}\end{array}\end{array}$$

傅里叶变换讨论

傅里叶变换性质

1.物理空间的离散对应傅里叶空间的有界。
2.物理空间的有界对应傅里叶空间的离散。
对于结论一，我们假定两个复函数为$f(x)=e^{i{k}_{1}x},g(x)=e^{i{k}_{2}x}$，且其中的$k_1\ne k_2$，$x$是定义在离散空间$h\mathbf{Z}$的网格点$x_j=jh,j\in \mathbf{Z}$上的，则：
$$\begin{array}{c}\begin{array}{r}{f}_j=e^{i{k}_1{x}_j}\\ g_j=e^{i{k}_2{x}_j}\end{array}\end{array}$$如果$k_1-k_2$是$\frac{2\pi }{h}$的倍数，则对于每个$j$有$f_j=g_j$。由此可见，对于任何复指数$e^{ikx}$，有无限的其他复指数与它匹配的网格$h\mathbf{Z}$ 。因此，在长度为$\frac{2\pi }{h}$的区间内测量网格的波数就足够了，由于对称性的原因，我们选择区间$[-\frac{\pi }{h},\frac{\pi }{h}]$。
对于结论二，可以通过傅里叶正反变换的对称性来理解，因为在傅里叶变换中，时间和空间是等价的。在傅里叶空间的离散，代入到傅氏反变换中，也是需要计算复指数函数的，同理也会导致物理空间的有界$[0,2\pi ]$。
假定空间上的网格点数$N$是偶数，则网格点的间距是$h=2\pi /N$，可得：
$$\begin{array}{c}\begin{array}{r}\frac{\pi }{h}=\frac{N}{2}\end{array}\end{array}$$现在，傅里叶域是离散的和有界的。这是因为物理空间中的波必须在区间$[0,2\pi ]$上是周期性的，并且只有具有整数波数的$e^{ikx}$具有所需的周期$2\pi$。

aliasing phenomenon

快速傅里叶变换（fft）的性质

这里讨论的是MATLAB中使用的fft和ifft。在使用这些程序时必须稍微小心一点，因为MATLAB假设波数的顺序与我们的不同。在我们的符号中使用的波数表示为：
$$\begin{array}{c}\begin{array}{r}{\hat{f}}_{-\frac{N}{2}+1},{\hat{f}}_{-\frac{N}{2}+2}\cdots ,{\hat{f}}_{\frac{N}{2}}\end{array}\end{array}$$因为fft的使用使用了一个复杂的转换用来匹配该变换满足对称特性${\hat{f}}_j={\hat{f}}_{-j}$,这是由大多数傅里叶变换所利用的，它只存储了大约一半的数组，减少了保持系数所需的内存，并使速度提高了大约两倍，此时傅里叶空间中的傅里叶系数为：
$$\begin{array}{c}\begin{array}{r}{\hat{f}}_0,{\hat{f}}_1,\cdots ,{\hat{f}}_{\frac{N}{2}}\end{array}\end{array}$$

傅里叶系数排列

设$L=Nh$表示仿真域的物理长度。然后，真正的波数数组就采用了这种形式
$$\begin{array}{c}\begin{array}{r}k(i)=\{\begin{array}{ll}\frac{2\pi }{L}i,& i=1,\cdots ,\frac{N}{2}\\ \frac{2\pi }{L}(-N+i)& i=\frac{N}{2}+1,\cdots ,N\end{array}\end{array}\end{array}$$下图是16点，间距为1的傅里叶变换系数的分布情况：

$${\hat{f}}_k$$

伪谱法的稳定性

当用伪谱法数值求解时变偏微分方程时，其模式通常是相同的：空间上的谱微分，时间上的有限差分。例如，人们可以通过欧拉格式来执行时间步进。
以变系数波动方程为例：
$$\begin{array}{c}\begin{array}{r}{\partial }_{t}u=c{\partial }_{x}u,c={\sin }^2(x-1)+0.2,u_0=e^{-100(x-1{)}^2}\end{array}\end{array}$$求解它的迭代格式为：
$$\begin{array}{c}\begin{array}{r}{u}^{n+1}=u^n-2\Delta tc{F}^{-1}[ikF(u)]\end{array}\end{array}$$当时间步长为$\frac{h}{4}=0.0491$时，它是稳定的。

稳定情况

但是当$\Delta t>\frac{1.9}{N}$时，它的解就变得不稳定了。这里的不稳定性是由于时间离散引起的，可以通过适当的隐式离散化来规避。

不稳定情况

伪谱法的频散现象

与有限差分法相比，傅里叶方法最显著的特点之一是数值色散小。设置同样的参数进行伪谱法与三点、五点有限差分实验，通过对比波传播相同时间到达相同位置情况下频率不同引起的频散现象来研究各种算法的频散特性，下面显示快照允许我们得到两个重要结论，实验结果如下：

从图中可以看出随着子波主频的不断增加，不论是三点还是五点有限差分，它们的频散现象愈发严重，且五点有限差分频散较三点有所改善。相比之下，伪谱法的频散现象随主频增大不是很严重，几乎不存在频散。伪谱法理论上不会出现频散现象，我们在数值实验中出现频散是因为时间上作了差分离散导致的频散，跟稳定性一样可以使用其他形式的时间离散来进行改进。
从c组图中可以看出，有限差分解具有明显的强各向异性色散行为。最准确的方向出现在$\theta =45°$，伪谱法解没有表现出明显的色散，但最重要的是，它似乎没有方向依赖性。也就是说，误差是各向同性的。
关于频散性的结论，下图也可以明显说明：

频散性比较

吉布斯现象

吉布斯现象是由亨利·威尔伯拉罕在1848年发现的，然后由j·威拉德·吉布斯在1899年重新发现。
对于具有不连续的周期信号，如果通过加傅立叶级数来重构信号，则在边缘附近会出现超调。这些超调以远离边缘的阻尼振荡方式向外衰减。这被称为GIBBS现象，如下图所示。

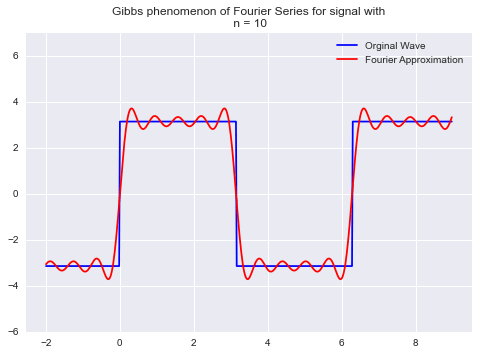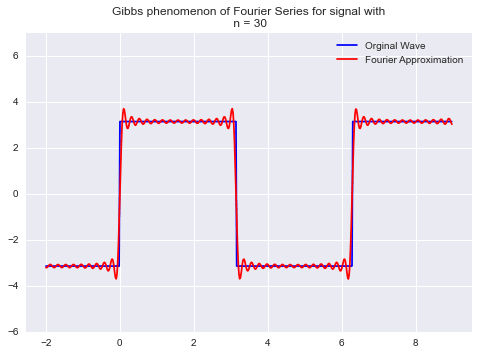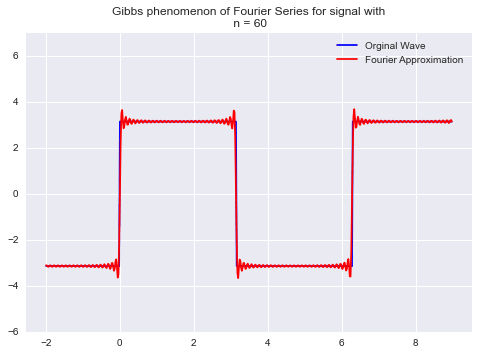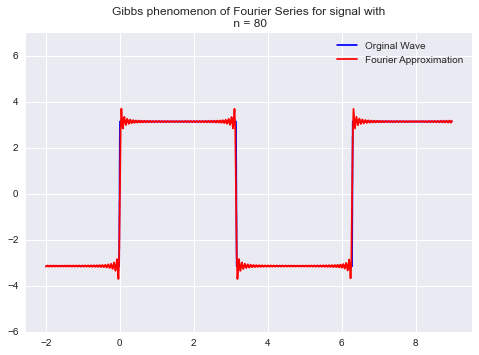
因为，当$0<x<\pi$时$f(x)=1$，当$\pi <x<2\pi$时$f(x)=-1$(在$(0,2\pi )$范围外重复)定义的方波具有傅立叶级数展开:
$$\begin{array}{c}f(x)=\frac{4}{\pi }\sum _{n=1,3,5,\cdots }\frac{1}{n}\sin (nx)\end{array}$$更一般的,随着N增加，部分起伏就向不连续点压缩，但是对任何有限的N值，起伏的峰值大小保持不变，以函数$f(x)=x$为例，其周期为$2\pi$，某个定义区间为$[-\pi ,\pi ]$,其图像为：

且它的傅里叶展开级数的系数为：
$$\begin{array}{c}\begin{array}{rl}{b}_n& =(\frac{1}{\pi }){\int }_{-\pi }^{\pi }x\sin (nx)\mathrm{d}x\\ & =(-1{)}^{n+1}(\frac{2}{n})\end{array}\end{array}$$则它的傅里叶级数近似结果如下：

其误差表示为：

从图中可以看出其误差最大值保持不变，约为跳变值的0.09倍。
当使用伪谱法求导数是使用的不是函数一整个周期时，求导结果也会出现吉布斯现象，例如在区间$[0,2\pi ]$上求取$\cos (x)$的导数（它的一个完整周期应该是$[0,2\pi )$，不包含$2\pi$）时会出现吉布斯现象。

伪谱法对sin函数求导