多种类多元素有序分组问题

例子

18 个标准小球（红9、黄6、蓝3），有序分成 10 组，组不允许为空，有几种方案？

---

讨论

如果允许组为空，比较简单，直接用插板法求解。
n 个小球分成 10 组，即 n+10-1 个间隔中选择 10-1 个插入隔板，方案数为：
C(n+10-1,10-1) = C(n+9,9)
三种颜色小球的方案数叠加（乘积）就是总方案数：
C(9+9,9)×C(6+9,9)×C(3+9,9) = 53535482000

如果不允许组为空（这个前提更贴近实际情形），可以用插板法+容斥原理求解。
对于 i 个组为空的情形，其方案数为：
G(i)
= C(10,i)×C(9+9-i,9-i)×C(6+9-i,9-i)×C(3+9-i,9-i)
= C(10,i)×C(18-i,9-i)×C(15-i,9-i)×C(12-i,9-i)
运用容斥原理，总方案数为：
Sum [ (-1)^i × G(i) ]，( i = 0～9 )
= 2100657730

---

代码

计算组不为空情形的 Python 和 Fortran 代码

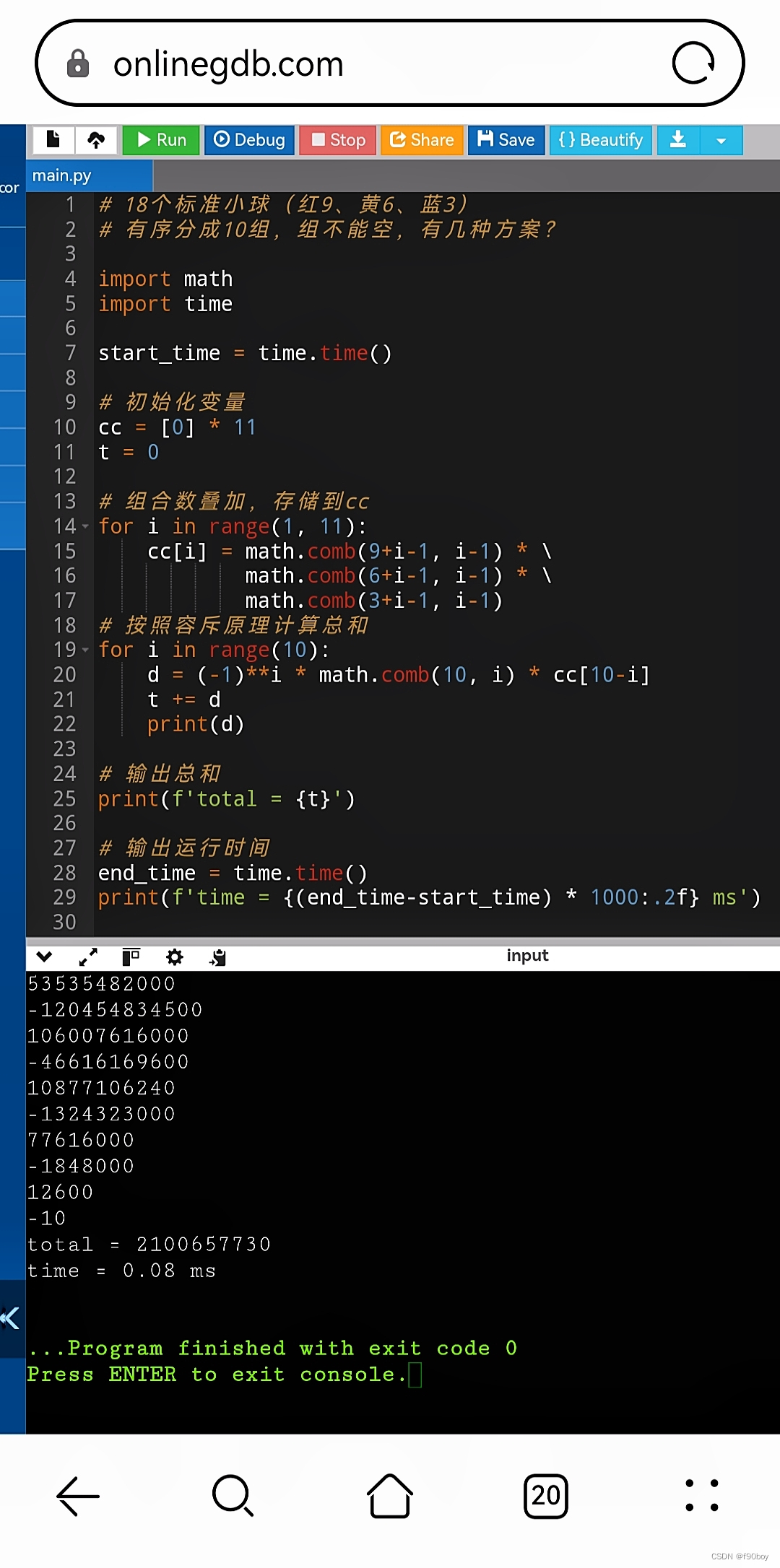
Python

# 18个标准小球（红9、黄6、蓝3）
# 有序分成10组，组不能空，有几种方案？

import math
import time

start_time = time.time()

# 初始化变量
cc = [0] * 11
t = 0

# 组合数叠加，存储到cc
for i in range(1, 11):
    cc[i] = math.comb(9+i-1, i-1) * \
            math.comb(6+i-1, i-1) * \
            math.comb(3+i-1, i-1)
# 按照容斥原理计算总和
for i in range(10):
    d = (-1)**i * math.comb(10, i) * cc[10-i]
    t += d
    print(d)

# 输出总和
print(f'total = {t}')

# 输出运行时间
end_time = time.time()
print(f'time = {(end_time-start_time) * 1000:.2f} ms')

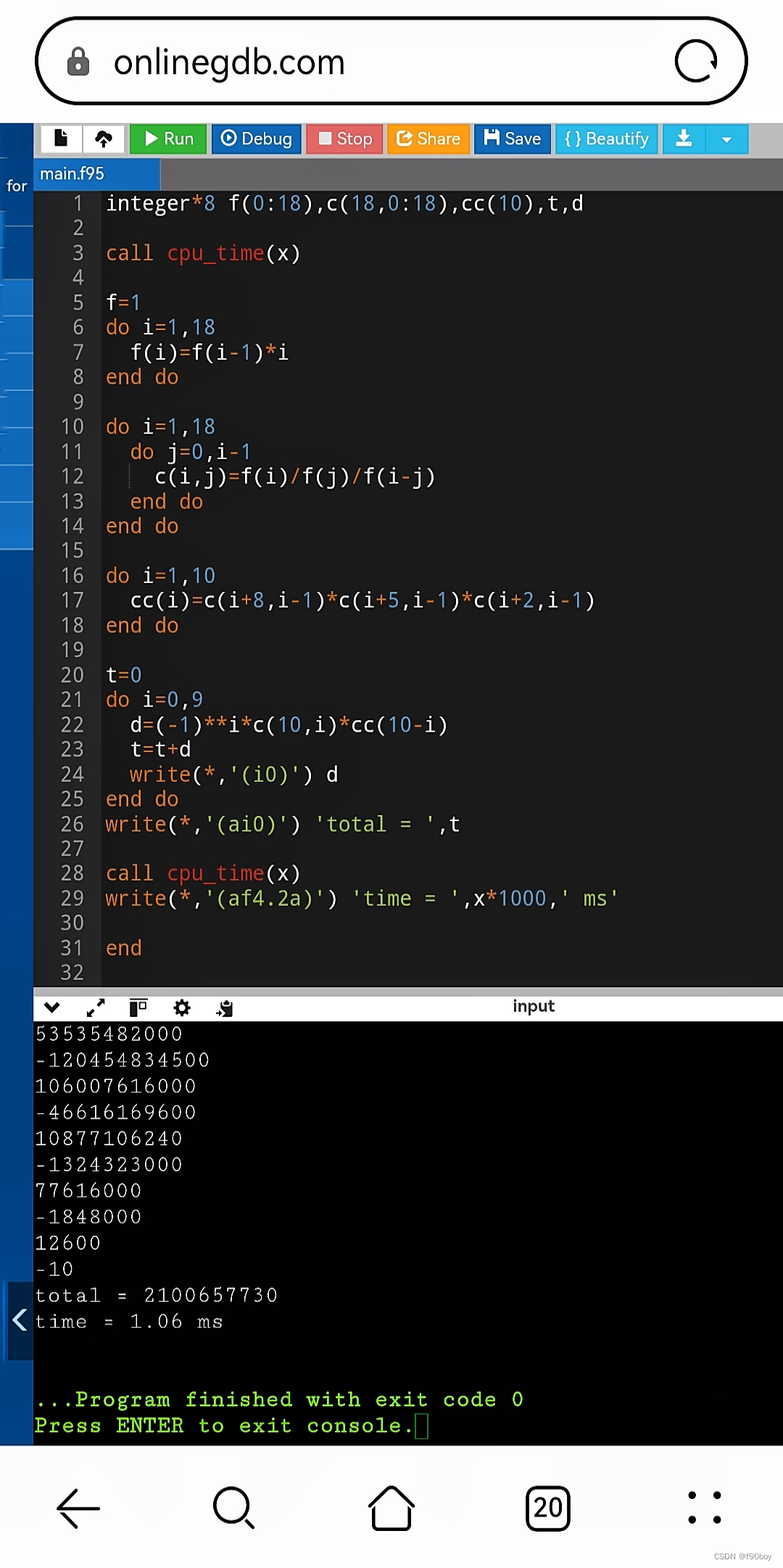
Fortran

integer*8 f(0:18),c(18,0:18),cc(10),t,d

call cpu_time(x)

f=1
do i=1,18
  f(i)=f(i-1)*i 
end do 

do i=1,18
  do j=0,i-1
    c(i,j)=f(i)/f(j)/f(i-j)
  end do 
end do

do i=1,10
  cc(i)=c(i+8,i-1)*c(i+5,i-1)*c(i+2,i-1)
end do

t=0
do i=0,9
  d=(-1)**i*c(10,i)*cc(10-i)
  t=t+d 
  write(*,'(i0)') d
end do 

write(*,'(ai0)') 'total = ',t
call cpu_time(x)
write(*,'(af4.2a)') 'time = ',x*1000,' ms'

end

---

在线编译运行的截图