散列表（哈希表）

概念

散列表和map函数的原理差不多，是根据键值对（key，value）就能直接访问的数据结构，key和value之间存在着一种映射的关系，这个映射函数就叫散列函数，而储存的数组才是散列表，value可以是一个值，也可以是一个链表，如果要处理散列表的冲突问题就要使用到链表。

映射之间转化原理

1. 通过散列函数公式转化为整型类型，然后再用数组长度来对这个整型进行求余，求余的结果就是数组下标，用这个下标值来存放value。
2. 压缩映射：把任意长度的输入，用固定函数来转化成一个固定长度的值，而且这个值远小于输入长度的值。但是这个方法很容易出现离散表的冲突问题。

散列函数的方法主要是3种：

1. 除法散列法：直接使用公式1：index = value % 16 ​​​​​​，求余就是一种除法运算
2. 平方散列法：在计算机运算中，乘法是比除法的计算效率快的（虽然现在的CPU强到看不到就是了），所以也可以使用公式2：index = (value * value) >> 28，（>>右移操作就是相当于除法运算，意义是除以2^28），如果value*value溢出怎么办呢，这里取的是运算结果的值，不需要value*value的值，所以就算溢出，问题不大。
3. 斐波那契散列法：那如果我们能找到一个理想的乘数就不需要使用本身的value值了，那这个理想乘数对于不同位数也会不同，对于16位整数而言，这个乘数是40503 ，对于32位整数而言，这个乘数是2654435769 ，对于64位整数而言，这个乘数是11400714819323198485，例如对于一个32位数的整数，使用公式3： index = (value * 2654435769) >> 28。

我们之所以要使用不同的散列函数，是因为要实现均匀存储。

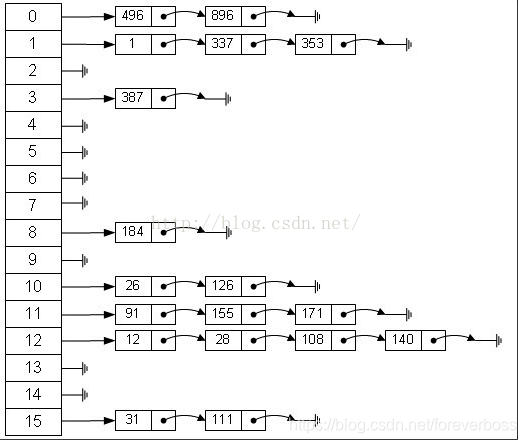
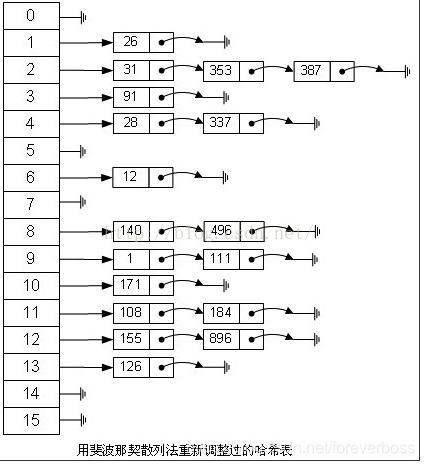
散列冲突

我们为什么要实现均匀存储呢，主要是为了避免出现冲突的情况，当不同的关键字经过散列函数得到同样的散列地址时，就是散列冲突。

解决方案：

1. 建立缓冲区，当我们得到相同的散列地址时，我们就会在缓冲区中寻找。
2. 再次进行探测，当然探测的方法也有3种：
   1. 在index周围中寻找，例如在index+1，index-1，然后是index+-2，以此类推。
   2. 在index周围中随机寻址。
   3. 使用别的散列函数来再次哈希

散列表的应用

1. 主要是用于安全的加密算法
2. 快速查找，哈希表在查找的时间复杂度是O(1)
3. 在处理大量数据的操作中，也可以使用

总结

优点：

1. 哈希表无论是在查找，插入，删除等操作的效率都比较快，这结合了数组和链表的优点。
2. 哈希表适合于处理大数据

缺点：

哈希表虽说结合了链表和数组的优点，但是始终是基于数组的数据结构，所以但存储的数据大于定义的数组长度时，效率会急促的下降。