摩尔投票法的个人理解

摩尔投票法的个人理解

摩尔投票法是找出多数元素的算法；
多数元素是出现次数大于n/2的元素；
摩尔投票法就是进行抵消和 合并的过程，首先选定第一个元素，接着往后遍历，若相同则+1，不同则-1。如果为0，就更换为新元素。

由于具体原理和实现其他文章写得很详细，所以在这里就说一下我个人对这个方法的个人理解：

用诸国混战比喻：

1. 先给视觉给到第一个国家的士兵（第一个数组元素），并给这名士兵一盏灯。
2. 这个国家的士兵散布在战场的各处；(设每支队伍数为count，初始count=1)

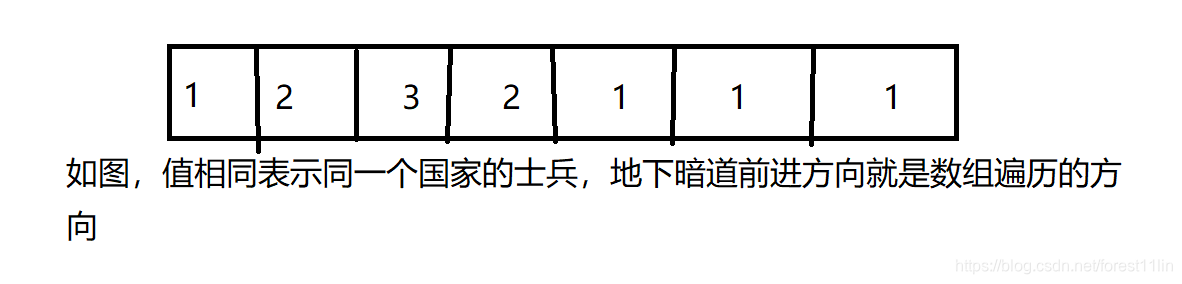
假设这个战场是一地下暗道（数组），暗道里的士兵（数组中的各个元素）互相都看不到对方，于是都互相提防，按兵不动；只有第一个士兵拥有灯，能看清前方的士兵是敌国的还是本国的；各国的士兵都是势均力敌的，即若对决则会同归于尽。

首先，在我们的视角里，这名拿着灯的士兵往战场走去。（与数组后一位元素比较）

1. 若是前方是本国的士兵，则将灯交给对方，由对方在前方探路，本国的队伍+1；（值相等count+1）
2. 若前方是敌国的士兵（无论哪国都是敌国），则探路的士兵会与对方同归于尽，这时灯掉落在地上，本国后面的士兵会捡起来继续向前。本国队伍-1；（值不等count-1）
3. 若本国的这只队伍全部牺牲，则前方的士兵（可能是本国也可能是敌国）会捡起灯，这时我们的视觉就转向捡起灯的士兵。（若count=0，当前元素=新数组元素）

最后存活走出战场的士兵所在的国家（即多数元素）就是最后的胜利者。（count>0，则当前元素为多数元素）