算法学习之二叉排序树的平衡化

最新推荐文章于 2023-02-10 20:53:58 发布

原创最新推荐文章于 2023-02-10 20:53:58 发布 · 819 阅读

2 ·

CC 4.0 BY-SA版权

文章标签：

#学习

本文探讨了为何需要平衡二叉排序树，如何通过旋转操作（右旋和左旋）保持树的平衡，以及关键的AVL树平衡化算法。通过实例和代码演示了如何确保查询效率，避免树结构退化为数组。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

首先提出问题：问什么要让二叉树排序树平衡化

比如给出{1,2,3,4,5,6,7}让我们将其构造成排序树，如下图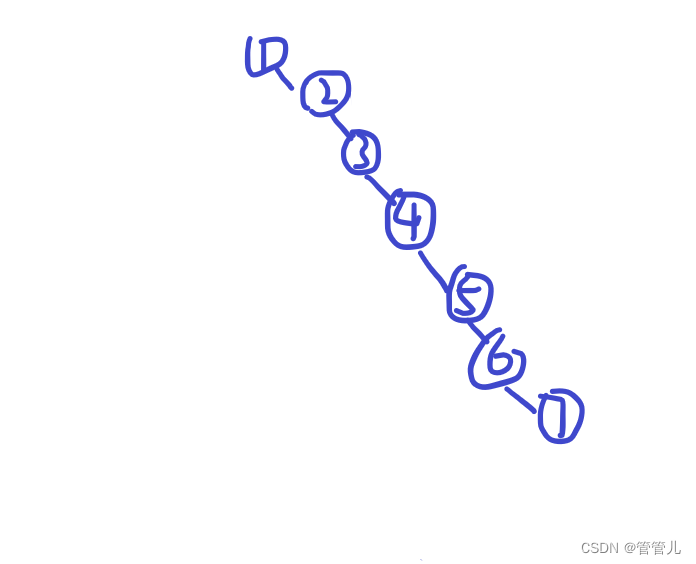

可以看出，此时二叉树变成了数组，而我们为了提高搜索效率的初衷也被打破了

为了解决这种极端情况，我们需要对二叉树进行平衡化

概念

每个节点的左子树和右子树的高度差至多为一
必须是二叉查找树
高度是从根节点到目标节点的层数

思路

我们需要查询出从根节点开始其左右子节点的高度

若左子树的高度-右子树高度>1,该节点右旋
若右子树的高度-左子树高度>1,该节点左旋
右旋的步骤
- 让该节点的左节点更为新的根结点，即该节点的左子节点指向左子树的右子树,该节点的左子树的右子节点指向该节点,在用父节点指向新的节点
左旋的步骤
- 让该节点的右节点更为新的根结点，即该节点的右子节点指向右子树的左子树,该节点的右子树的左子节点,指向该节点,在用父节点指向新的节点

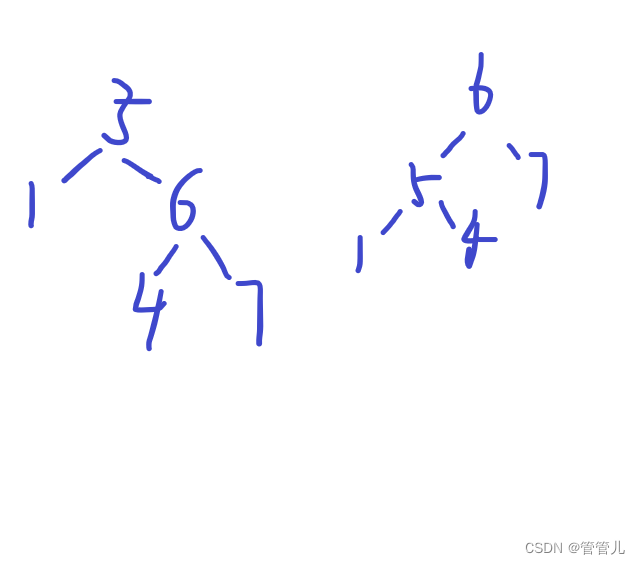
进行右旋时,节点左子树的右子树高度大于左子树的左子树高度时,其左子树要先左旋,既保证左子树高度大于右子树高度

进行左旋时,节点右子树的左子树高度大于右子树的右子树高度时,其右子树要先右旋,既保证右子树高度大于左子树高度

代码

class BinaryNode {

    /**
     * 查找父节点
     * @param node
     * @return
     */
    public BinaryNode getFatherNode(BinaryNode node) {
        BinaryNode node1 = null;
        if (this.left != null) {
            if (this.left == node) {
                node1 = this;
                return node1;
            }else {
                node1 = this.left.getFatherNode(node);
            }
        }
        if (node1 != null) {
            return node1;
        }
        if (this.right != null) {
            if (this.right == node) {
                node1 = this;
                return node1;
            }else {
                node1 = this.right.getFatherNode(node);
            }
        }
        return node1;
    }

    /**
     * 查询节点的高度
     * @return 该节点的高度
     */
    public int highOfNode() {
       return Math.max(left == null ? 0 : left.highOfNode(),right == null ? 0 : right.highOfNode()) + 1 ;
    }

    /**
     * 左子树的高度
     * @return 如果左节点为空,返回0,反之返回高度
     */
    public int leftHigh() {
        if (this.left == null) {
            return 0;
        }else {
            return left.highOfNode();
        }
    }

    /**
     * 右子树的高度
     * @return 如果右节点为空,返回0,反之返回高度
     */
    public int rightHigh() {
        if (this.right == null) {
            return 0;
        }else {
            return right.highOfNode();
        }
    }
}
class BinarySortTree {

    /**
     * 左旋转,使根结点的右节点成为新的根结点,原来根结点的右节点指向新根节点的左节点
     * 这样可以使当前树的左子树高度加一,右子树高度减一
     */
    public void leftRotation(BinaryNode node){
        // 方案一
        // 1.创建一个新的节点,newNode值等于根节点的值
//        BinaryNode node = new BinaryNode(root.getValue());
//        // 2.把新节点的左子树设置为根节点的左子树
//        node.left = root.left;
//        // 3.把新节点的右子树设置为根结点的右子树的左子树
//        node.right = root.right.left;
//        // 4.把根结点的值换为右子节点的值
//        root.setValue(root.right.getValue());
//        // 5.把根节点的右子树设置为右子树的右子树
//        root.right = root.right.right;
//        // 6.把当前节点的左子树设置为新节点
//        root.left = node;
        // 方案2
        // 找到其父节点
        boolean flag = true;
        BinaryNode fatherNode = getFatherNode(node);
        if (fatherNode != null && fatherNode.left != null && fatherNode.left == node) {
            flag = false;
        }
        // 左旋,该节点的右子树指向右子树的左子树,该节点的右子树的左子树,指向该节点,在用父节点指向新的节点
        BinaryNode index = node;
        BinaryNode newNode = node.right;
        node.right = newNode.left;
        newNode.left = index;
        if (node == root) {
            root = newNode;
        }else if (flag) {
            fatherNode.right = newNode;
        }else {
            fatherNode.left = newNode;
        }
    }


    /**
     * 右旋转,使根结点的左节点成为新的根结点,原来根结点的左节点指向新根节点的右节点
     * 这样可以使当前树的左子树高度减一,右子树高度加一
     */
    public void rightRotation(BinaryNode node) {
        boolean flag = true;
        BinaryNode fatherNode = getFatherNode(node);
        if (fatherNode != null && fatherNode.left != null && fatherNode.left == node) {
            flag = false;
        }
        BinaryNode index = node;
        BinaryNode newNode = node.left;
        node.left = newNode.right;
        newNode.right = index;
        if (node == root) {
            root = newNode;
        }else if (flag) {
            fatherNode.right = newNode;
        }else {
            fatherNode.left = newNode;
        }
    }

    /**
     * 顺序二叉树平衡化,平衡化是指每个节点的左子树和右子树的高度差至多为一
     * @param node
     */
    public void avl(BinaryNode node) {
        // 当左子树高度 - 右子树高度 > 1时,右旋,使左子树高度减一,右子树高度加一
        if ((node.leftHigh() - node.rightHigh()) > 1) {
            // 当节点左子树的右子树高度大于左子树的左子树高度时,其左子树要先左旋,既保证左子树高度大于右子树高度
            if (node.left != null && node.left.rightHigh() > node.left.leftHigh()) {
                leftRotation(node.left);
                rightRotation(node);
            }else {
                rightRotation(node);
            }
        }
        // 当右子树高度 - 左子树高度 > 1时,左旋,使右子树高度减一,左子树高度加一
        if ((node.rightHigh() - node.leftHigh()) > 1) {
            // 当节点右子树的左子树高度大于右子树的右子树高度时,其右子树要先右旋,既保证右子树高度大于左子树高度
            if (node.right != null && node.right.leftHigh() > node.right.rightHigh()) {
                rightRotation(node.right);
                leftRotation(node);
            }else {
                leftRotation(node);
            }
        }
        if (node.left != null) {
            avl(node.left);
        }
        if (node.right != null) {
            avl(node.right);
        }
    }

}