用 Kotlin 做对比，就是插 Comparable 啦！嫁接这姐，你就可以货比三家。

最新推荐文章于 2025-10-29 15:55:59 发布

原创最新推荐文章于 2025-10-29 15:55:59 发布 · 2.5k 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#kotlin #面试

Kotlin 专栏收录该内容

6 篇文章

订阅专栏

本文通过Kotlin的Comparable接口，详细介绍了compareTo()、coerceAtLeast()、coerceAtMost()和coerceIn()等方法的使用，并结合BinarySearchTree的应用，展示了如何在Kotlin中进行比较和操作。文章包含多个实例演示，适合面试复习和学习。

💪0. 比较神器——Comparable

👸VS👸🏻，🙅Fight！叽里咕噜…
比较这个嗜好，女人们最喜欢，比上比下，比房子比车子，甚至比子女。
👀：在 Kotlin 世界里，你插这个就能比，就是 Comparable 插件。

🏎️1. 方程 compareTo()

compareTo() 是主打方程，发出比一比的号角。
这个 class 是地主🐢，compareTo( 对手🐰 )。

👧🏻：这不是龟兔赛跑吗？好玩！
🤔：这个比喻不好，不明白，咱还是画圈吧。

介绍个两个免费网上Kotlin 编译器 ——

Kotlin Playground 游乐园 —— 这个快👍。
JDoodle —— 怪名。现打现用，今天就是用这个面试废了。我不是应聘写手机的吗？考官就考基础。我就琢磨着这是干什么来着，手机只有两个问题，其它全是 order，sort，linked list, binary search，可能银行就喜欢这个。记性不好，明年再来。哈奇😷！

✔️它们好处是现打现用，❌坏处是编译功能缺失。你们谁能写个 AI 补补？
…

class Circle(val radius: Int): Comparable<Circle> { 
    private val area: Double = 3.14 * radius * radius
    
    override fun compareTo(other: Circle): Int { 
        val area2 = other.area
  
        // 对比面积
        if(area == area2){ 
            return 0; 
        } else if(area < area2){ 
            return -1; 
        } 
        return 1; 
    } 
    
    override fun toString(): String {
        return "Type(circle) -> radius = $radius, area = $area"
    }
}

fun main(){ 
    val cirs: List<Circle> = listOf(
        Circle(5), Circle(4), Circle(4), Circle(7), Circle(8), Circle(10)) 
  
    println("Is cir1 > cir2? ${cirs[0] > cirs[1]}") 
    println("Is cir3 > cir1? ${cirs[2] > cirs[1]}")
    println("Is cir3 == cir1? ${cirs[2] == cirs[1]}")
}

这个 compareTo 需要覆盖，因为 Comparable 只是个 Interface，骨头也。它要做出三种答复 ——

等于 ⇨ 0
小于 ⇨ -1
大于 ⇨ 1

简单，明快。
结果：

Is cir1 > cir2? true
Is cir3 > cir1? false
Is cir3 == cir1? false

🚝2. 方程 coerceAtLeast() 较大

这是比最小大一点的意思，例子：
coerceAtLeast( 较大 )：

是问我比最小大吗？—— 是就我上，反之最小上。

咱们试试：

    var min = Circle(2) 
    var max = Circle(9) 
    
    println("\nmin: ${min}\ncir2: ${cirs[1]}")    
    println("Find bigger: cir1 > min? Bigger is ${cirs[1].coerceAtLeast(min)}")

🏃结果：

min: Type(circle) -> radius = 2, area = 12.56
cir2: Type(circle) -> radius = 4, area = 50.24
Find bigger: cir1 > min? Bigger is Type(circle) -> radius = 4, area = 50.24

➕找个大小差不多看看：

    println("\ncir1: ${cirs[0]}\ncir2: ${cirs[1]}")    
    println("Find bigger: cir1 > cir2? Bigger is ${cirs[0].coerceAtLeast(cirs[1])}") 
    println("Find bigger: cir2 > cir1? Bigger is ${cirs[1].coerceAtLeast(cirs[0])}")

🏃结果：

cir1: Type(circle) -> radius = 5, area = 78.5
cir2: Type(circle) -> radius = 4, area = 50.24
Find bigger: cir1 > cir2? Bigger is Type(circle) -> radius = 5, area = 78.5
Find bigger: cir2 > cir1? Bigger is Type(circle) -> radius = 5, area = 78.5

都是较大的胜出，这就是 coerceAtLeast 。

🚈3. 方程 coerceAtMost() 较小

顾名思义，coerceAtMost() 就比最大小点，较小也。

    println("\ncir5: ${cirs[4]}\nmax: ${max}")    
    println("Find bigger: cir5 > max? Bigger is ${cirs[4].coerceAtMost(max)}") 
    println("Find bigger: cir5 > max? Bigger is ${max.coerceAtMost(cirs[4])}")

比对 8 号选手和 max 选手。

cir5: Type(circle) -> radius = 8, area = 200.96
max: Type(circle) -> radius = 9, area = 254.34
Find bigger: cir5 > max? Bigger is Type(circle) -> radius = 8, area = 200.96
Find bigger: cir5 > max? Bigger is Type(circle) -> radius = 8, area = 200.96

8 号较小胜出。现在看来好像多余，其实不是，思维有点不一样而已。反正又不用我写，用就是了。

🚅4. 方程 coerceIn() 域内

明白不？这个方程当然有一大一小，要不怎么知道是否在队伍内。
例子：

coerceIn( 最小，最大 )

拿来玩玩：

    println("\ncir4: ${cirs[3]}\nmin: ${min}\nmax: ${max}")    
    println("Is cir4 in min and max? ${cirs[3].coerceIn(min, max) == cirs[3]}")

在室吗？🏃🏼

cir4: Type(circle) -> radius = 7, area = 153.86
min: Type(circle) -> radius = 2, area = 12.56
max: Type(circle) -> radius = 9, area = 254.34
Is cir4 in min and max? true

做两个域外的：

[ ✔️ ] X < min

    min = Circle(6)
    println("\ncir1: ${cirs[0]}\nmin: ${min}\nmax: ${max}")    
    println("Is cir1 in min and max? ${cirs[0].coerceIn(min, max)}")

🏃🏼：

cir1: Type(circle) -> radius = 5, area = 78.5
min: Type(circle) -> radius = 6, area = 113.03999999999999
max: Type(circle) -> radius = 9, area = 254.34
Is cir1 in min and max? Type(circle) -> radius = 6, area = 113.03999999999999

证明在 min 方向，域外。
…

[ ✔️ ] X > max

    min = Circle(6)
    println("\ncir6: ${cirs[5]}\nmin: ${min}\nmax: ${max}")    
    println("Is cir6 in min and max? ${cirs[5].coerceIn(min, max)}")

🏃🏼：

cir6: Type(circle) -> radius = 10, area = 314.0
min: Type(circle) -> radius = 6, area = 113.03999999999999
max: Type(circle) -> radius = 9, area = 254.34
Is cir6 in min and max? Type(circle) -> radius = 9, area = 254.34

max 方向，域外。

🚀5. 对比应用 BinarySearchTree

BinarySearchTree 是 LinkedList 的一种。用 node 节点法插，左右两只手，不是左就是右。
…
👳🏾（面试官）：你好！
🤓（老板派个不好相语的）：你好！
👳🏾：懂 Comparable 吗？
😅（&*#%￥，忘记大半）：嗯，懂的。
👳🏾：（敲键盘）按这个 List [ 8,10,9,2,1,5,4,6,7,3 ] 来，这是圆圈的半径。你用 Comparable 建一个 BinarySearchTree ，语言 Kotlin 。
😨（喔槽…万马奔腾呼啸而过！）：OK，我来推敲推敲…用半径啊…

Circle ：

class Circle(val radius: Int): Comparable<Circle> { 
    
    override fun compareTo(other: Circle): Int = 
    	when {
            radius == other.radius -> 0
            radius < other.radius -> -1
            else -> 1
        }
    
    override fun toString(): String = "Circle($radius)"
}

还可以，超简单的。
…

⭕️ 测试空车

来开个头：

class BinarySearchTree<T : Comparable<T>> {

	data class Node<T: Comparable<T>>(
		var data: T, 
		var left: Node<T>? = null,
		var right: Node<T>? = null
	) {
	}
	
	var root: Node<T>? = null

BinaryTree 当然是太极 ☯️ 分俩仪，data class 是 Kotlin 简化版 class 类别。加点印刷 🖨️ 能力：

	data class Node<T: Comparable<T>>(
		var data: T, 
		var left: Node<T>? = null,
		var right: Node<T>? = null
	) {     
        override fun toString(): String = 
        	"\tdata($data),\n<-($left),\t->($right)\n"
    }

	var root: Node<T>? = null
	
	override fun toString() = root?.toString() ?: "empty tree"

🌽 main：

fun main(){ 
    
    val cirs: List<Circle> = listOf(
        Circle(8), Circle(10), Circle(9), 
        Circle(2), Circle(1), Circle(5), 
        Circle(4), Circle(6), Circle(7),
        Circle(3)
    ) 
        
    val bt: BinarySearchTree<Circle> = BinarySearchTree<Circle>()    
    println("BT: $bt")
}

🙉Run：

BT: empty tree

活的！这是好的开始。
😆：考官，后面用说的成不？
👳🏾（你考还是我考？)：🐽，用 insert() 插入数据。
😆：呵呵，来啦来拉…
…

♈️ 插入测试

    fun insert(value: T) {
        root?.apply { insert(value) } ?: 
        	run { root = Node(value) }
    }

?: 是干啥的？左边应该是 非NULL，就是有东西，进 Data Class 里面那个 insert() 寻找方向；右边是没有东西，直接插新值。

	data class Node<T: Comparable<T>>(
        var data: T, 
        var left: Node<T>? = null,
        var right: Node<T>? = null
	) {     
        override fun toString(): String = ...
        
        fun insert(value: T) { // <= 左边；> 右边
			if (value <= data) { 
				left?.insert(value) ?: run { left = Node(value) }
			} else {
				right?.insert(value) ?: run { right = Node(value) }
			}
		}
    }

🌽 main：

    for (c in cirs) { bt.insert(c) }
    println("BT: $bt")

🙉Run：

BT: 	data(Circle(8)),
<-(	data(Circle(2)),
<-(	data(Circle(1)),
<-(null),	->(null)
),	->(	data(Circle(5)),
<-(	data(Circle(4)),
<-(	data(Circle(3)),
<-(null),	->(null)
),	->(null)
),	->(	data(Circle(6)),
<-(null),	->(	data(Circle(7)),
<-(null),	->(null)
)
)
)
),	->(	data(Circle(10)),
<-(	data(Circle(9)),
<-(null),	->(null)
),	->(null)
)

🙄：难看点，左右还能插对了，好了。
👳🏾：加 contains() 作搜寻，找 8，7 和 11 。
😅：还有？接着了。
…

🕵搜索节点

照虎画猫，递牌子进 Data Class。
👵🏻：什么什么！你教坏小朋友，是照猫画虎。

    fun contains(value: T): Boolean {
        var found = false;
        root?.apply { 
            found = contains(value) 
        }
        return found
    }

💿 data class:

        fun contains(value: T): Boolean =
            when {
                value < data && left != null -> 
                	left!!.contains(value)
                value > data && right!=null ->
                	right!!.contains(value)
                else -> 
                	value.compareTo(data) == 0
            }

🌽 main：

...
    println("Search for Circle(8): ${bt.contains(Circle(8))}")
    println("Search for Circle(7): ${bt.contains(Circle(7))}")
    println("Search for Circle(11): ${bt.contains(Circle(11))}")

🙈Run：

Search for Circle(8): true
Search for Circle(7): true
Search for Circle(11): false

漫天神佛保佑，pass！
👳🏾：不错不错，加个 remove()，删除 8，3，10 。
😅（没完没了）：Sí，no problemo！
…

💣去除节点

mv8
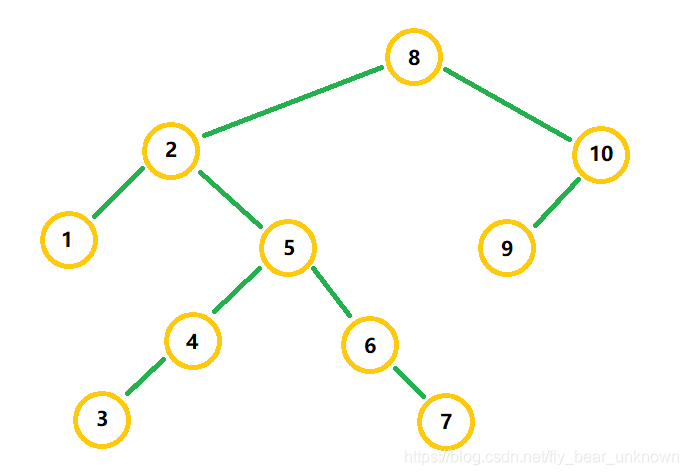
这个好复杂也，多种状况。
8 号置顶，大号骨头。两个仔。
3 号最底层，最简单。
10 号跟 3 号差不多。

💥去没仔的

🌽 main：

    bt.insert(Circle(8))
    println("BST: $bt")
    println("Removed circle(8): ${bt.remove(Circle(8))}")
    println("BST: $bt")

拿一个试手。
🌲 BinarySearchTree：

    fun remove(value: T): Boolean {
        root = remove(value, root)
        return !contains(value)
    }
    
    fun remove(value: T, parent: Node<T>?): Node<T>? {
        parent ?: return null
        
        when {
            parent.data.compareTo(value) == 0 -> {
                when {
                    // no left child
                    parent.left == null -> {
                        return parent.right
                    }
                    // no right child
                    parent.right == null -> {
                        return parent.left
                    }
                }
                // two children
                
            }
        }
        return parent        
    }

🐵Run：

BST: 	data(Circle(8)),
<-(null),	->(null)

Removed circle(8): true
BST: empty tree

👳🏾（在试？)：🐽，继续看手机。
…

💥去单仔：只有右边

🌽 main：

    bt.insert(Circle(8))
    bt.insert(Circle(9))
    
    println("BST: $bt")
    println("Removed circle(8): ${bt.remove(Circle(8))}")
    println("BST: $bt")

🐵Run：

BST: 	data(Circle(8)),
<-(null),	->(	data(Circle(9)),
<-(null),	->(null)
)

Removed circle(8): true
BST: 	data(Circle(9)),
<-(null),	->(null)

Good！
…

💥去单仔：只有左边

🌽 main：

    bt.insert(Circle(8))
    bt.insert(Circle(7))
    
    println("BST: $bt")
    println("Removed circle(8): ${bt.remove(Circle(8))}")
    println("BST: $bt")

🐵Run：

BST: 	data(Circle(8)),
<-(	data(Circle(7)),
<-(null),	->(null)
),	->(null)

Removed circle(8): true
BST: 	data(Circle(7)),
<-(null),	->(null)

…

❌去两个仔的

mv8
现在去 8 号。
➕没找到的线路。
🌲 BinarySearchTree：

    fun remove(value: T, parent: Node<T>?): Node<T>? {
        parent ?: return null
        
        when {
            parent.data.compareTo(value) == 0 -> {
                when {
                    // no left child
                    parent.left == null -> {
                        return parent.right
                    }
                    // no right child
                    parent.right == null -> {
                        return parent.left
                    }
                }
                // two children
                
            }
            // less to left
            value < parent.data -> parent.left = remove(value, parent.left)
            // most to right
    		else -> parent.right = remove(value, parent.right)
        }
        return parent        
    }

➕找到的线路：

8 号要 9 号顶，叫右小（右边最小）。
Node Data Class 加 minNode：

	data class Node<T: Comparable<T>>(
        var data: T, 
        var left: Node<T>? = null,
        var right: Node<T>? = null
	) {
        ...   
        // right min:
        val minNode: Node<T>?
  			get() = left?.minNode ?: this
    }

remove(value: T, parent: Node?) 里面：

            parent.data.compareTo(value) == 0 -> {
                when {
                    // no left child
                    parent.left == null -> {
                        return parent.right
                    }
                    // no right child
                    parent.right == null -> {
                        return parent.left
                    }
                }
                // two children
                val rightMin = parent.right?.minNode!!
                println("Right minimum: ${rightMin.data}")
                
            }

🐵Run：

Right minimum: Circle(9)

找到了，接收 8号的遗产。

            parent.data.compareTo(value) == 0 -> {
                when {
                    // no left child
                    parent.left == null -> {
                        return parent.right
                    }
                    // no right child
                    parent.right == null -> {
                        return parent.left
                    }
                }
                // two children
//                 val rightMin = parent.right?.minNode!!
//                 println("Right minimum: ${rightMin.data}")
//              // move value of rightMin up
				parent.right?.minNode!!.data?.let {
                    parent.data = it
                }
                // remove rightMin
                parent.right = remove(parent.data, parent.right)

🌽 main：

    for (c in cirs) { bt.insert(c) }
    println("Removed circle(8): ${bt.remove(Circle(8))}")
    println("BST: $bt")

🐒Run：

Removed circle(8): true
BST: 	data(Circle(9)),
<-(	data(Circle(2)),
<-(	data(Circle(1)),
<-(null),	->(null)
),	->(	data(Circle(5)),
<-(	data(Circle(4)),
<-(	data(Circle(3)),
<-(null),	->(null)
),	->(null)
),	->(	data(Circle(6)),
<-(null),	->(	data(Circle(7)),
<-(null),	->(null)
)
)
)
),	->(	data(Circle(10)),
<-(null),	->(null)
)

连续去 8号， 3号，10号。
🌽 main：

    println("Removed circle(8): ${bt.remove(Circle(8))}")
    println("Removed circle(3): ${bt.remove(Circle(3))}")
    println("Removed circle(10): ${bt.remove(Circle(10))}")
    println("BST: $bt")

🐒Run：

Removed circle(8): true
Removed circle(3): true
Removed circle(10): true
BST: 	data(Circle(9)),
<-(	data(Circle(2)),
<-(	data(Circle(1)),
<-(null),	->(null)
),	->(	data(Circle(5)),
<-(	data(Circle(4)),
<-(null),	->(null)
),	->(	data(Circle(6)),
<-(null),	->(	data(Circle(7)),
<-(null),	->(null)
)
)
)
),	->(null)

😂：好了，好了。
👳🏾：很好，省得改题了，你加个 asSortedList() 方程，分别印顺次，和反向的次序。
😵：Sort， sort， sort，怎么写？来啦…
…

♐️ Sort

🌲 BinarySearchTree：

    fun asSortedList(): List<T> = root?.toList() ?: emptyList()

让 root 去搜货。
💎 Node Data Class ：

        fun toList(): List<T> = listOfNotNull(
                left?.toList(),
                listOf(data), 
                right?.toList()).flatten()

listOfNotNull() 是只收 NotNull 的货。瞧，我收左边的 toList()，左边最小；再收现在这个；然后收右边的 toList() 。BST就这好，从左到右不用再 sort 。
flattern() 就是把 X 条 List 合成一条新的 List 。

🌽 main：

    val mlist = bt.asSortedList()
    println("Sorted list: ${mlist}")

🐒Run：

Sorted list: [Circle(1), Circle(2), Circle(3), Circle(4), Circle(5), Circle(6), Circle(7), Circle(8), Circle(9), Circle(10)]

反向， 🌽 main：

    val revlist = mlist.asReversed()
    println("Reversed Order list: ${revlist}")

🐒Run：

Reversed Order list: [Circle(10), Circle(9), Circle(8), Circle(7), Circle(6), Circle(5), Circle(4), Circle(3), Circle(2), Circle(1)]

…

🍋. 结果

👳🏾：正确，但是时间到了，但是这里还有几道题，我会向上级汇报你的情况，你回去等消息吧。祝你好运！
😬：谢谢！你也一样。