Circle Loss: A Unified Perspective of Pair Similarity Optimization
2020年CVPR的一篇文章,Circle Loss: A Unified Perspective of Pair Similarity Optimization[1],文章非常的好(๑•̀ㅂ•́)و✧,很久没看过这么干货的文章了。Circle Loss指出softmax loss类和triplet loss类损失函数的同质性,并提出了一种囊括softmax loss类学习和Triplet loss样本对学习的统一损失,且可以重新配比每个相似度,自适应地专门强调欠优化的相似度得分项,提供一种更灵活的优化策略,来打破这样的同质性。Circle Loss也在包括人脸识别,行人重识别等图像检索数据集中达到了新的SOTA。
论文一览:

痛点
作者认为常用的Triplet Loss和softmax+cross entropy loss没有区别,都是在最小化类间相似度,最大化类内相似度(扩大类间距离,缩小类内距离),这两种loss并没有本质的区别。换句话说,他们也共享着相似的优化模式,即减小(Sn(负样本对距离)-Sp(正样本对距离))。这带来了两个问题:
1)优化缺乏灵活性
限制在 s n s_{n} sn和 s p s_{p} sp上的惩罚强度(penalty strength)是相等的。给定一个损失函数, s n s_{n} sn和 s p s_{p} sp的梯度具有几乎相同的幅值。
2)收敛状态不明确
优化 s n − s p s_{n}-s_{p} sn−sp会得到决策边界 s n − s p = m s_{n}-s_{p}=m sn−sp=m,这样的决策边界是模糊的,如下图1(a)中的T和T‘:
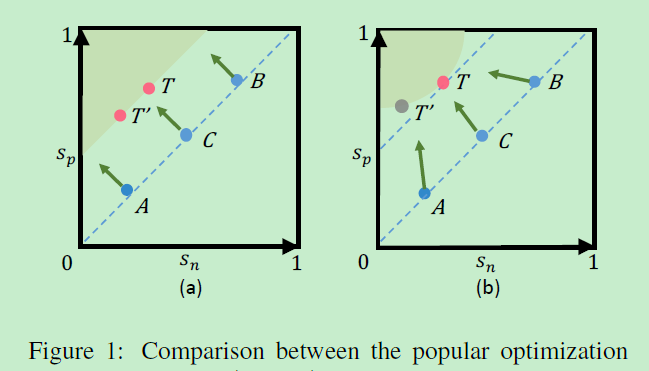
例如当T为{ s n , s p s_{n}, s_{p} sn,sp}={ 0.2 , 0.5 0.2, 0.5 0.2,0.5},而T’为{ s n ′ , s p ’ s_{n}',s_{p}’ sn′,sp’}={ 0.4 , 0.7 0.4, 0.7 0.4,0.7},他们的间隔margin都为0.3。然而全局来看, s n ′ s_{n}' sn′到 s p s_{p} sp的距离只有0.1,这样的决策边界显然是不合理的,可以看到这样的收敛导致到特征空间的分离,没有办法兼顾到全局空间。
作者认为不同的相似度分数应具有不同的惩罚强度,设计了 ( α n S n − α p S p ) (α_{n}S_{n}-α_{p}S_{p}) (αnSn−αpSp)的优化模式, α n α_{n} αn和 α p α_{p} αp独立的权重因子,使得Sn与Sp以不同的步幅学习,使学习节奏适应优化状态:离最优越远的相似度得分,权重因子就越大。这样的决策边界 ( α n S n − α p S p = m ) (α_{n}S_{n}-α_{p}S_{p}=m) (αnSn−αpSp=m)会在 s n s_{n} sn, s p s_{p} sp空间中产生一个圆形,这也是Circle Loss名称的由来。如图1的(b),A为强调提高 s p s_{p} sp,B为强调减小 s n s_{n} sn,这使得优化目标将更加明确
本文的贡献主要为:
1)提出了Circle Loss,通过重新配比相似度得分的权重,使得深度特征的学习更灵活,优化目标更加明确。
2)Circle Loss兼容类级标签和样本对标签,且经过细微的修改可退化为Triplet loss和Softmax Loss。
3)Circle Loss在多种图像检索任务中如人脸识别,行人重识别和汽车图像检索等任务达到了新的SOTA。
模型
1)统一Triplet和softmax的损失函数
假设有K个类内相似度得分(一个batch同一行人有K张图),L个类间相似度得分(一个batch一共有L个行人)。他们的相似性得分分别为{ s p i s_{p}^{i} spi} ( i = 1 , 2... , K ) (i=1, 2..., K) (i=1,2...,K)和 { s n j s_{n}^{j} snj} ( j = 1 , 2... , L ) (j=1, 2..., L) (j=1,2...,L),则定义统一的损失函数如下:
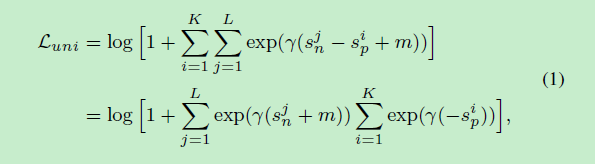
其中γ是尺度因子,m为分离相似度的margin。公式(1)遍历每一个相似对来减少 ( s n j − s p i ) (s_{n}^{j}-s_{p}^{i}) (snj−spi)。
2)退化为Softmax loss
设计算x和权重向量
w
i
(
i
=
1
,
2
,
.
.
.
,
N
)
w_{i}(i=1,2,...,N)
wi(i=1,2,...,N)的相似度得分(N为训练的类的数量),则有N-1个类间(余弦)相似度得分:
s
n
j
=
w
j
T
x
/
(
∣
∣
w
j
∣
∣
∣
∣
x
∣
∣
)
s_{n}^{j} = w_{j}^{T}x/(||w_{j}||||x||)
snj=wjTx/(∣∣wj∣∣∣∣x∣∣)
(
w
j
w_{j}
wj为第j个非目标类的权重向量)还有1个类内的(余弦)相似度得分:
s
p
=
w
y
T
x
/
(
∣
∣
w
y
∣
∣
∣
∣
x
∣
∣
)
s_{p} = w_{y}^{T}x/(||w_{y}||||x||)
sp=wyTx/(∣∣wy∣∣∣∣x∣∣)。
根据这些条件,可以将公式(1)退化为AM-softmax[2]:
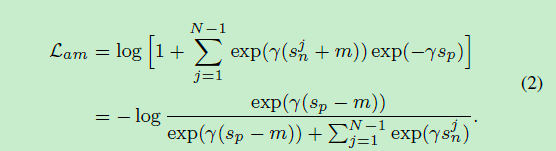
若m=0,(2)式退化成Normface[3]。若用内积替换余弦相似度,再令γ=1,则最终退化为softmax:
L = − l o g e x p ( s p ) e x p ( s p ) + ∑ j = 1 N − 1 e x p ( s n j ) = − l o g e x p ( w y ⋅ x ) e x p ( w y ⋅ x ) + ∑ j = 1 N − 1 e x p ( w j ⋅ x ) = − l o g e x p ( w y ⋅ x ) ∑ j = 1 N e x p ( w j ⋅ x ) L = -log\frac{exp(s_{p})}{exp(s_{p}) + \sum\nolimits_{j=1}^{N-1}exp(s_{n}^{j})} \\ = -log\frac{exp(w_{y} \cdot x)}{exp(w_{y} \cdot x) + \sum\nolimits_{j=1}^{N-1}exp(w_{j} \cdot x)} \\ = -log\frac{exp(w_{y} \cdot x)}{\sum\nolimits_{j=1}^{N}exp(w_{j} \cdot x)} L=−logexp(sp)+∑j=1N−1exp(snj)exp(sp)=−logexp(wy⋅x)+∑j=1N−1exp(wj⋅x)exp(wy⋅x)=−log∑j=1Nexp(wj⋅x)exp(wy⋅x)
3)退化为Triplet Loss
计算feature之间的相似度,负样本对有: s n j = x j T x / ( ∣ ∣ x j ∣ ∣ ∣ ∣ x ∣ ∣ ) s_{n}^{j} = x_{j}^{T}x/(||x_{j}||||x||) snj=xjTx/(∣∣xj∣∣∣∣x∣∣),对正样本对有: s p i = x i T x / ( ∣ ∣ x i ∣ ∣ ∣ ∣ x ∣ ∣ ) s_{p}^{i} = x_{i}^{T}x/(||x_{i}||||x||) spi=xiTx/(∣∣xi∣∣∣∣x∣∣)。
式(1)退化为triplet loss有:
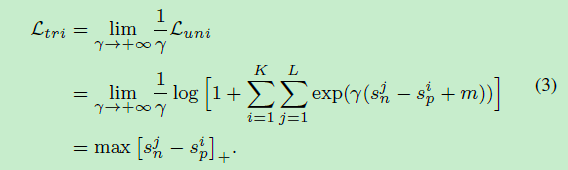
逐渐增大γ将逐渐增加样本mining的强度,当γ趋于无穷大时,式(3)就变成标准的triplet hard mining loss。
由此可见Triplet hard loss及其变种,和softmax loss及其变种,都是式(1)的特殊情况。
4)对比Triplet/Softmax loss的梯度
不同loss梯度对比如下图(这个图非常棒):
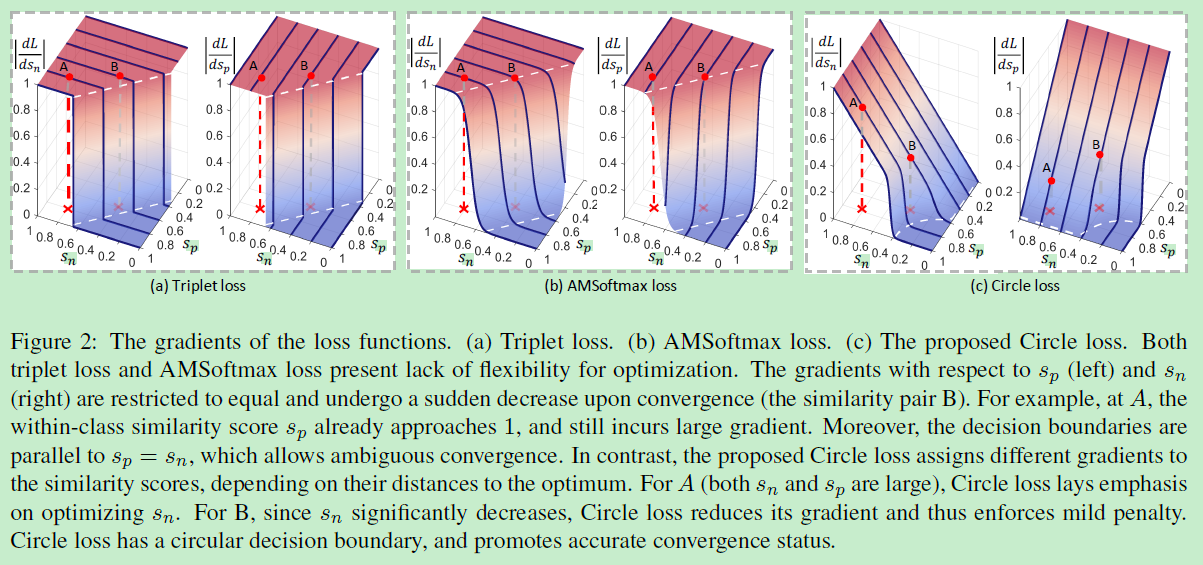
可以看到如图2(a),左边Z轴是 s n s_{n} sn的梯度,右边Z轴是 s p s_{p} sp的梯度。可知:
1)loss到达决策边界之前, s n s_{n} sn和 s p s_{p} sp的梯度是差不多的,而且loss收敛之前梯度面近乎平坦,然后会经历非常大的下降来收敛。
2)图中所示的A点 s n s_{n} sn和 s p s_{p} sp均为0.8,但是梯度仍然非常大。B点相对于A点更靠近决策边界,所以比A点是优化的更好一点点,但是要记得softmax和triplet对A B施加的惩罚是一样的,所以这样A B的优化偏差几乎会一直持续。
3)决策边界与 S n − S p = m S_{n}-S_{p}=m Sn−Sp=m是平行的,还记得图1中任意两点到决策边界都有相似度距离m,换言之,loss函数最小化 S n − S p = m S_{n}-S_{p}=m Sn−Sp=m对于不同的点(T和T’)是无差别的,也更倾向于模糊收敛(而没有针对性)。
triplet/softmax loss存在这么多的问题,那这些问题是怎么导致的?作者认为所有的问题归根结底来自于最小化 s n − s p s_{n} - s_{p} sn−sp的优化方式——这导致减小 s n s_{n} sn和增大 s p s_{p} sp是等价的。
5)Circle Loss
基于统一的Loss(式1),作者为不同的相似度得分(similarity score)添加独立的权重因子 α n α_{n} αn和 α p α_{p} αp,先忽略margin m的情况下得到了(简单版)Circle Loss:
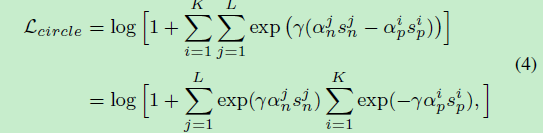
α n α_{n} αn和 α p α_{p} αp是非负数。Circle Loss主要是将 ( s n − s p ) (s_{n}-s_{p}) (sn−sp)拓展为了 ( α n s n − α p s p ) (α_{n}s_{n}-α_{p}s_{p}) (αnsn−αpsp)。训练时, ( α n s n − α p s p ) (α_{n}s_{n}-α_{p}s_{p}) (αnsn−αpsp)的梯度将会乘 α n α_{n} αn或 α p α_{p} αp再反向传播给 s n s_{n} sn或 s p s_{p} sp。当 s n s_{n} sn或 s p s_{p} sp中的任何一方优化不够时,通过权重因子 α n α_{n} αn或 α p α_{p} αp会给优化不足的相似度得分一方提供更大的梯度以弥补不足。
对于margin的情况,使用 ( s n − s p ) (s_{n}-s_{p}) (sn−sp)时margin可以加强优化。但就正如前面讲的一样,margin分别对于 s n s_{n} sn和 s p s_{p} sp是等效的,所以传统的方法只有一个margin m,也只需要一个margin m。
但在Circle Loss中, s n s_{n} sn和 s p s_{p} sp时分离的,因此需要单独分别给margin,就有:
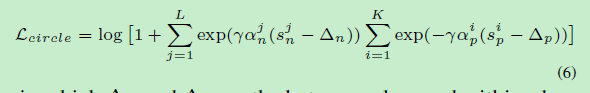
其中 Δ n \Delta_{n} Δn和 Δ p \Delta_{p} Δp分别为类间间隔和类内间隔,式(6)需要 s p i > Δ p s_{p}^{i} > \Delta_{p} spi>Δp, s n j < Δ n s_{n}^{j} < \Delta_{n} snj<Δn。设 s n j s_{n}^{j} snj和 s p i s_{p}^{i} spi的最优值为 O n O_{n} On和 O p O_{p} Op( O n O_{n} On< O p O_{p} Op)。则权重因子可以表示为:
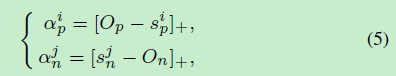
符号 [ ] + []_{+} []+是到零截断,相当于ReLU,保证权重因子的非负性。
则对于二分类问题(为了方便分析,所以选二分类问题),当达到 α n ( s n − Δ n ) − α p ( s p − Δ p ) = 0 α_{n}(s_{n}-\Delta_{n})-α_{p}(s_{p}-\Delta_{p})=0 αn(sn−Δn)−αp(sp−Δp)=0时,有决策边界:
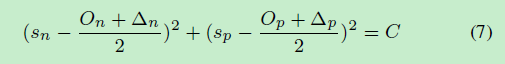
可以看到,决策边界是圆弧!就正如图1(b)和图2(c)所示!是不是感觉amazing!圆半径为 C \sqrt{C} C,圆心为 s n = ( O n + Δ n ) / 2 s_{n}=(O_{n}+\Delta_{n})/2 sn=(On+Δn)/2, s p = ( O p + Δ p ) / 2 s_{p}=(O_{p}+\Delta_{p})/2 sp=(Op+Δp)/2。
6)削减超参数
则Circle Loss有五个超参数, O p O_{p} Op, O n O_{n} On, γ \gamma γ, Δ p \Delta_{p} Δp和 Δ n \Delta_{n} Δn。文章减少超参数:令 O p = 1 + m O_{p}=1+m Op=1+m, O n = − m O_{n}=-m On=−m, Δ p = 1 − m \Delta_{p}=1-m Δp=1−m和 Δ n = m \Delta_{n}=m Δn=m。带入式(7)有新的决策边界:
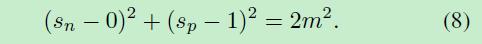
根据式(8)决策边界我们知道其优化目标是使 s p → 1 s_{p}→1 sp→1, s n → 0 s_{n}→0 sn→0。而参数m控制着决策边界的半径,可以被看做松弛因子。换言之Circle Loss希望 s p i > 1 − m s_{p}^{i}>1-m spi>1−m和 s n j < m s_{n}^{j}<m snj<m。这样超参数减少到了只有γ和m这两个。
7)对比Circle Loss的梯度
对Circle Loss的 s p s_{p} sp和 s n s_{n} sn分别求梯度有:
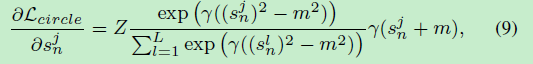
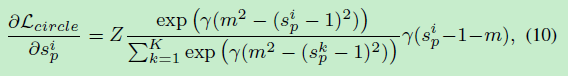
其中Z为:
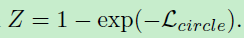
在二分类问题中,根据梯度得到图2(c):
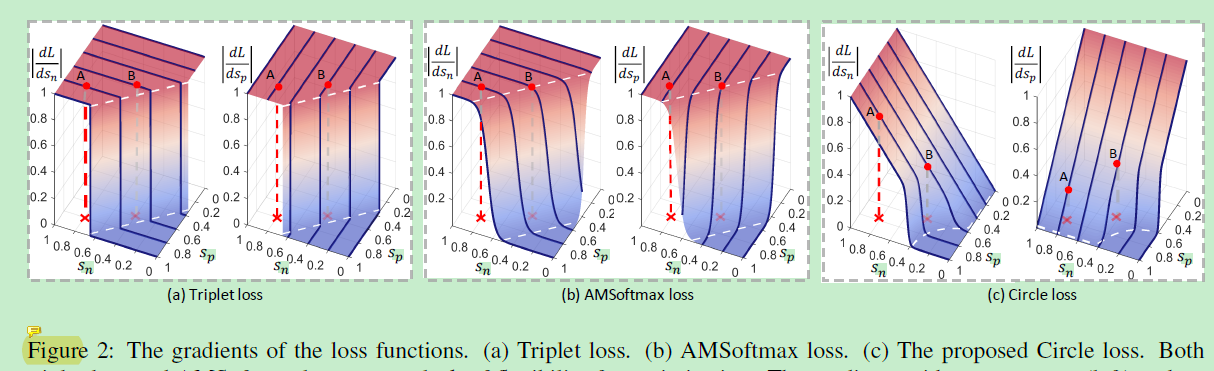
可以看到Circle Loss是对 s p s_{p} sp和 s n s_{n} sn的均衡优化,拿图2(c)左图的A点来说,虽然A点的{ s p , s n s_{p},s_{n} sp,sn}均为{ 0.8 , 0.8 0.8, 0.8 0.8,0.8},由于A点状态对 s n s_{n} sn的梯度较大,所以此时Circle Loss更趋向于使优化往减小 s n s_{n} sn的方向进行,这样的gradient平面对于 s n s_{n} sn来说是剧烈的下降,而对 s p s_{p} sp来说变化不大。
总体而言Circle Loss的技术特点主要有:
1)对正样本对相似度得分 s p s_{p} sp和负样本对相似度得分 s n s_{n} sn的平衡优化
2)为梯度下降提供自动衰减的梯度渐变
3)相比 s n − s p s_{n}-s_{p} sn−sp更明确的优化目标和相似度分布
实验
文章实验在多种学习方式地数据集中测试,包括类标签学习如人脸识别,行人重识别和成对标签学习如细粒度图像检索。
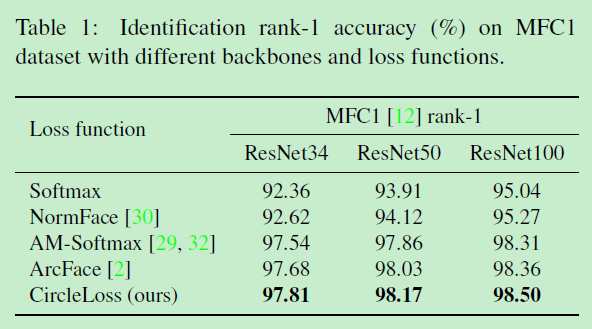
在人脸识别数据集MFC1(MegaFace Challenge 1)的横向SOTA对比:
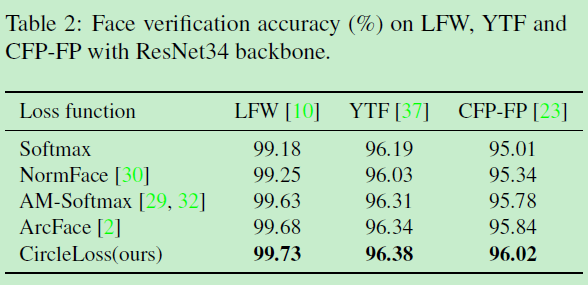
在人脸识别数据集LFW,YTF和CFP-FP的横向SOTA对比:
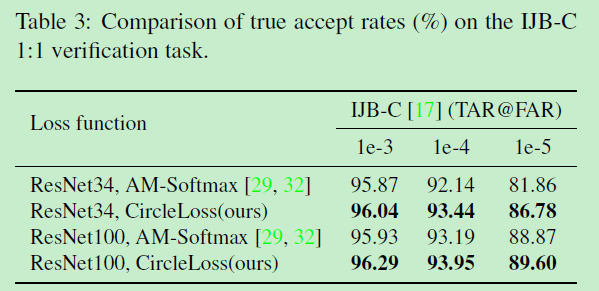
在IJB-C的横向SOTA对比:
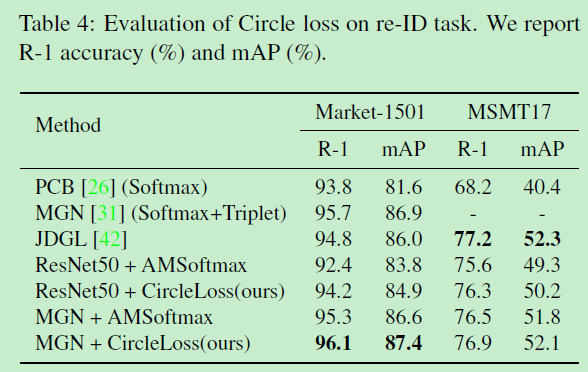
在行人重识别数据集Market1501和MSMT17的SOTA对比:
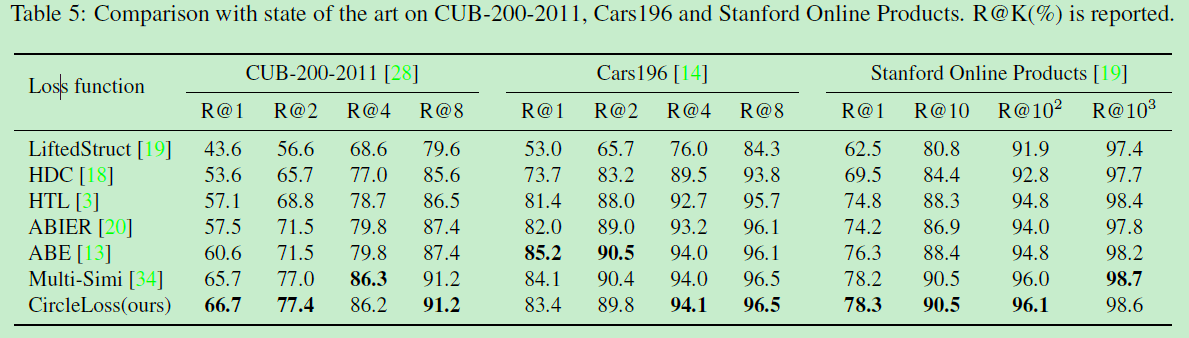
在细粒度图像检索数据集CUB-200-2011,Cars196,Stanford Online Products的SOTA对比:
超参数γ和松弛因子m对模型影响的分离实验,及与其他loss的横向对比,数据集为人脸库MFC1:
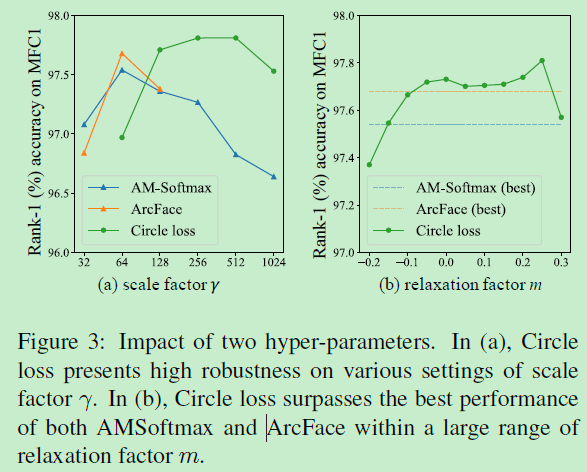
尺度因子γ确定每个相似性评分的最大比例。可以看到相比AM-softmax和ArcFace这两个loss,circle loss对γ有更高的鲁棒性,而作者认为原因主要是自动的梯度衰减导致,权重和梯度会自动衰减,从而保持适度的优化。而松弛因子m主要决定了决策边界的半径,可以看到在一段范围内Circle loss都超过了AM-softmax和ArcFace,作者认为同样表现了很强的鲁棒性。
训练时 s p s_{p} sp和 s n s_{n} sn的变化可视化如下:
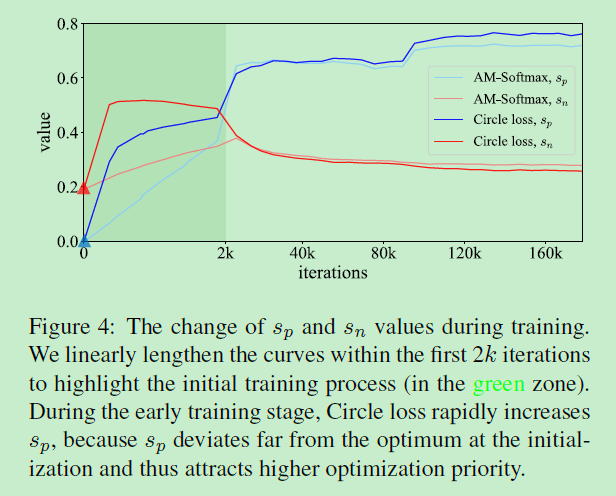
可以看到Circle Loss的 s p s_{p} sp和 s n s_{n} sn收敛速度要比AM-softmax要更快,且收敛后Circle Loss的 s n s_{n} sn比AM-softmax的 s n s_{n} sn要更小, s p s_{p} sp也比AM-softmax的 s p s_{p} sp要更大。
收敛后的相似度得分分布可视化如图:
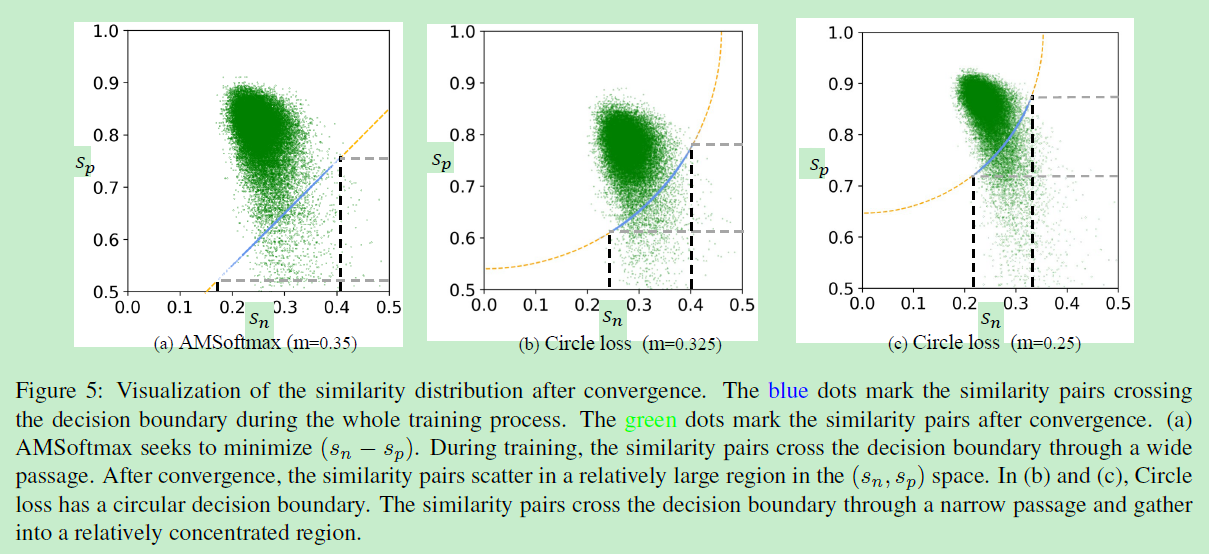
其中蓝色点线是在整个训练过程中标记跨越决策边界的相似度对,如图5(a)所示,AM-softmax追求最小化 s n − s p s_{n}-s_{p} sn−sp,在训练时,相似对通过广泛的通道越过决策边界,相似对的分布也松散。而看到(b)(c),Circle Loss是圆形的决策边界。相似对通过狭窄的通道越过决策边界,并聚集到相对集中的区域。
这表明与AM-Softmax相比,Circle Loss有助于所有相似对的更一致的收敛。 这种现象证实圆损失具有更确定的收敛目标,从而促进了特征空间中更好的可分离性。
写作
写作非常好,但是不知道怎么说。强烈推荐相关方向的自己细读。
感觉全程文章在带着读者走,看得很爽。
"
(Conclusion)First, a majority of loss functions, including the triplet loss and popular classification losses, conduct optimization by embedding the between-class and within-class similarity into similarity pairs. Second, within a similarity pair under supervision, each similarity score favors different penalty strength, depending on its distance to the optimum. These insights result in Circle loss, which allows the similarity scores to learn at different paces. The Circle loss benefits deep feature learning with high flexibility in optimization and a more definite convergence target.
"
非常好~~
问题
文章直接给出了统一的Loss函数式(式1),这个式子怎么来的?
参考文献
[1] Sun Y, Cheng C, Zhang Y, et al. Circle loss: A unified perspective of pair similarity optimization[J]. arXiv preprint arXiv:2002.10857, 2020.
[2] F. Wang, J. Cheng, W. Liu, and H. Liu. Additive margin softmax for face verification. IEEE Signal Processing Letters, 25(7):926–930, 2018.
[3] F. Wang, X. Xiang, J. Cheng, and A. L. Yuille. Normface: L2 hypersphere embedding for face verification. In Proceedings of the 25th ACM international conference on Multimedia,
pages 1041–1049. ACM, 2017.
[4] E. Hoffer and N. Ailon. Deep metric learning using triplet network. In International Workshop on Similarity-Based Pattern Recognition, pages 84–92. Springer, 2015.





 CircleLoss提出了一种统一的损失函数视角,融合了Triplet和Softmax损失,通过重新分配相似度得分权重,实现了更灵活的深度特征学习和更明确的优化目标。在人脸识别、行人重识别等任务上取得SOTA效果。
CircleLoss提出了一种统一的损失函数视角,融合了Triplet和Softmax损失,通过重新分配相似度得分权重,实现了更灵活的深度特征学习和更明确的优化目标。在人脸识别、行人重识别等任务上取得SOTA效果。



















 656
656












