10分钟搞懂决策树理论及编程—机器学习（监督学习）第一讲

最近在利用机器学习理论做一些具体的项目，系统的学习了一些机器学习的理论知识，准备系统的整理一下。当然为了做项目，自然也是要用到实际编程，会附上对应的代码。算是对理论学习的一个巩固和完善过程，希望对大家的学习也能有所帮助。

1.什么是决策树？

决策树是学习算法中最广泛应用的一种技术，这种算法的分类精准度与其它算法相比非常具有竞争力，实现效率也是非常高。算法的分类模型就是一棵树的形式，称之为决策树（Decision Tree），如图1所示。

决策树有两种类型的节点，决策节点（Decision Nodes，即中间节点）和叶子节点（Leaf Nodes）。最后到达的每一个叶子节点都是在对应的属性下的同类数据。一棵决策树就是通过属性参数不断分隔训练数据，使得各个子集尽量纯的过程。

图1 决策树模型

2.如何构建决策树？

对于同一组数据如果按照不同的划分方法可以构建不同的决策树，一棵决策树可以被转化为一系列的if—then关联规则。构造决策树的过程就是按照属性对数据进行递归分隔的过程，刚开始所有数据都在根部，随着决策树的“长大”，数据将不断的被分隔。每一次在属性的选择上，我们都选择最佳分类属性（根据混杂度函数计算得出）。混杂度函数反映了用该属性进行数据分隔以后的数据集的混杂度。

3.混杂度函数的计算

  最流行的用于决策树学习的混杂度函数是信息增益（Information Gain）和信息增益率（Information Gain Ratio）。信息增益是基于信息论（Information Theory）中熵的概念。

每一次选择属性分隔数据时，我们都希望能够让分类出来的数据更加纯，因此希望熵的改变最大，即信息增益最大，信息增益就是指熵的变化量。给出具体的公式如下（1-3）。

 图2 案例数据集

以图2中的数据集为例，我们在进行案例划分时怎么选择属性呢？是优先选择年龄还是是否有工作作为第一个决策节点呢？需要计算信息增益才能决定。整个表格中的数据集为D，它有四个属性：年龄、有工作、有房子、信贷情况，D中有6个否的训练实例和9个是的训练实例，可以计算得：

 然后我们用年龄这个属性对数据进行分隔，分隔之后的数据被分为三类，D1（青年）、D2（中年）、D3（老年），每个子集都是对应5个训练集。

=0.888

其中：=0.971

==0.971=0.722

 可以得到：*0.722=0.888

类似的可以得到：

=0.551，

=0.647，

=0.608

各个属性对应的信息增益分别为：

=0.971-0.888=0.083

=0.971-0.551=0.420

=0.971-0.647=0.324

=0.971-0.608=0.363

根据信息增益最大化原则，是否有房子是作为根节点的最好属性，后面继续采用这种方法对分类不纯的分支再进行数据分隔，最后就能得到整棵决策树。ID3决策树算法就是基于信息增益实现的。类似于信息增益，我们也可以选择信息增益率最大的属性作为最佳属性值。信息增益率的计算公式如式（4-5）所示。

                 （4）

            （5）

4.编程如何实现

通过自己编写计算信息增益的函数就可以每次都选出最佳属性，实现决策树构建过程。不过，决策树作为一种成熟的算法，在Matlab、Python语言开发等软件中都可以调用函数实现。本文以Matlab为例在程序中进行实现。部分代码如下：

%%

% 计算熵不纯度

function res = calculateImpurity(examples_)  %res就是信息熵

    P1 = 0;

    P2 = 0;

    [m_,n_] = size(examples_);             % 数据的行数和列数

    P1 = sum(examples_(:,n_) == 'yes');    % 分类标签为yes的数量

    P2 = sum(examples_(:,n_) == 'no');     %分类标签为no的数量，相加应该等于14

    P1 = P1 / m_;                          %计算所占的比例

    P2 = P2 / m_;

    if P1 == 1 || P1 == 0    %如果全是正例，则信息熵为0

        res = 0;

    else

        res = -(P1*log2(P1)+P2*log2(P2));  %信息熵的公式，计算整个数据的信息熵

    end

end

最后的运行结果如图3所示：

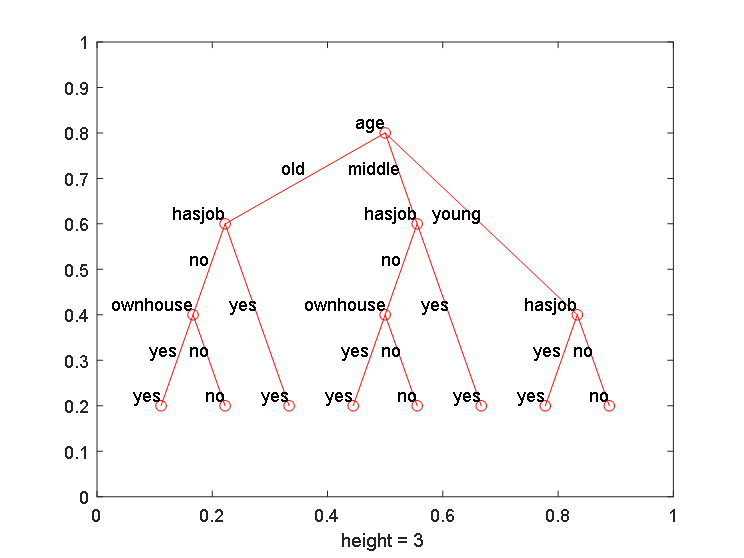
 图3  生成的决策树

如果以上内容对你的学习有所帮助，欢迎收藏、关注及评论。