【动态规划】路径问题动态

点赞👍👍收藏🌟🌟关注💖💖
你的支持是对我最大的鼓励，我们一起努力吧!😃😃

1.不同路径

题目链接：62. 不同路径

题目分析：

机器人每次只能向右或者向下走。问从起点到终点共有多少路径。

算法原理：

状态表示

根据经验 + 题目要求

经验都是以 i 位置为结尾，或者以 i 位置为起点，巴拉巴拉。但是这道题是二维的，所以 以[i，j]为结尾时，巴拉巴拉，题目要求问从起点到终点共有多少路径。所以
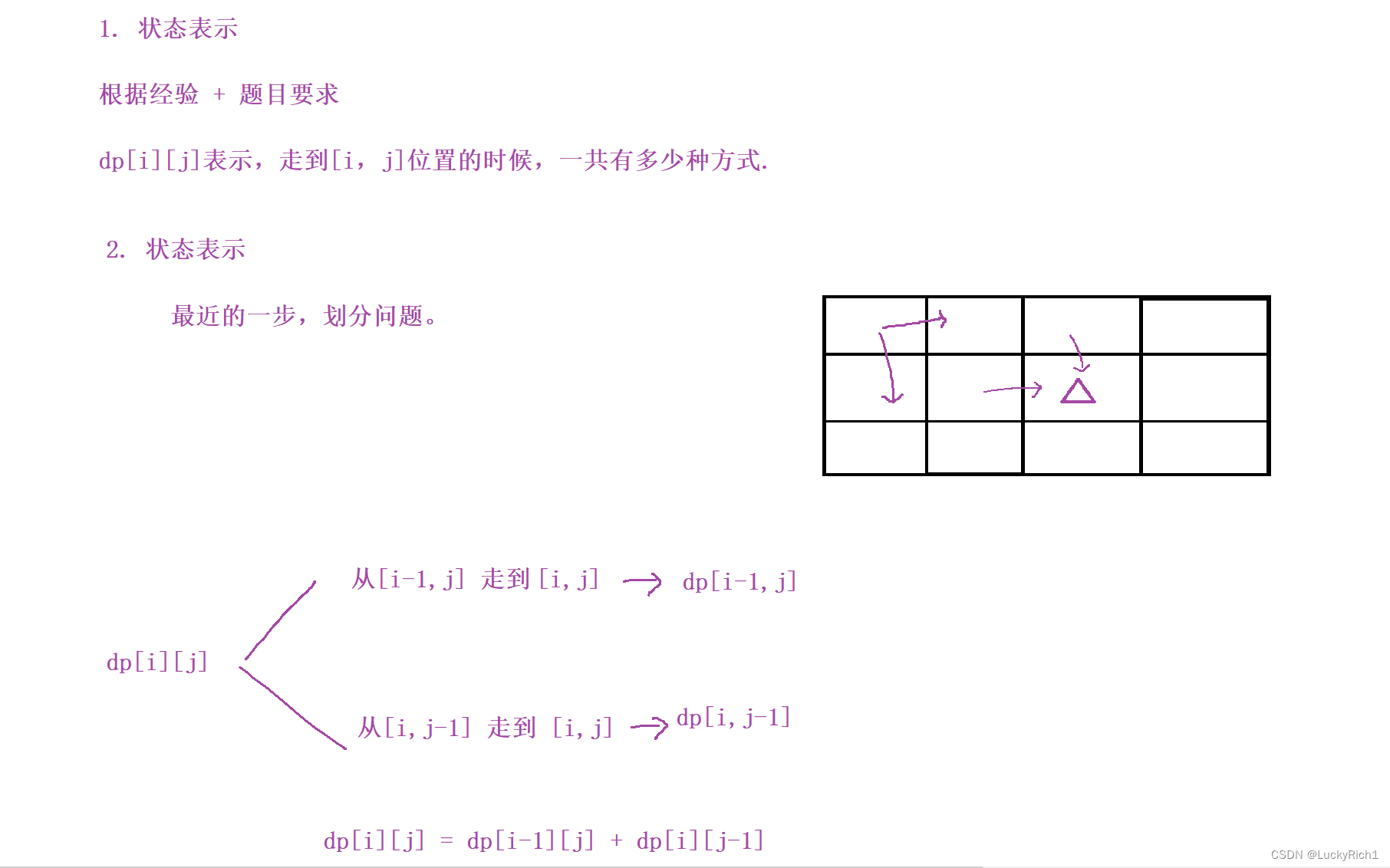
dp[i][j]表示，走到[i，j]位置的时候，一共有多少种方式。

状态转移方程

根据最近的一步，划分问题。

我们的问题是走到[i，j]的位置，那最近的一步就是如何走到[i，j]的位置，这道题只能向左向下走，因此走到[i，j]的位置分为两种情况。从[i-1，j]走到[i，j]，从[i，j-1]走到[i，j]。然后就看这两种情况能不能用状态表示。

从[i-1，j]走到[i，j]仅需在走一步就到[i，j]了，所以到[i-1，j]有多少种方法就知道从上面到[i，j]有多少种方法。那到[i-1，j]有多少种方法呢。而dp[i][j]表示就是走到[i，j]位置的时候，一共有多少种方式。所以dp[i-1，j] 可以表示从上面到[i，j]有多少种方法。

同理从[i，j-1]走到[i，j]也仅需再走一步就到[i，j]，dp[i，j-1] 表示从左边到[i，j]有多少种方法。

初始化

填表时不越界

根据状态转移方程填表我们发现填表需要用到上面的位置和左边的位置。但是填第一行和第一列就会发生越界的情况。

之前一维数组dp的时候说过有两种初始化的方式

1. 填表前先把越界的地方初始化
2. 一维数组前多开一个虚拟节点，繁琐的初始化就可以放在填表中进行，简单很多。

二维数组也可以这样做，直接多开一行一列！ 然后填表是就不会越界了。

但是要注意两个问题

1. 虚拟节点里面的值，要保证后面填表的结果是正确的
2. 下标的映射

虚拟节点的值应该填多少，具体问题具体分析。

这道题从起点到起点应该是1，从起点向左这一行也都是1，向下这一列也是1，那虚拟节点值填多少可以保证是这样的结果呢，我们发现只要把dp[0][1]这个虚拟位置初始化为1，其他初始化为0就可以了。

建议初始化，一维数组dp多开一个虚拟节点初始化，二维数组dp多开一行一列初始化。

填表顺序

从上往下填写每一行，每一行从左向后

返回值

题目要返回的是mn的位置，因为我们刚好多开一行一列，所以直接把dp[m][n]返回即可。

class Solution {
   
    int dp[101][101];
public:
    int uniquePaths(int m, int n) {
   
        // 1.创建dp表
        // 2.初始化
        // 3.填表
        // 4.返回值
        
        dp[0][1] = 1;
        for(int i = 1; i <= m; ++i)
        {
   
            for(int j = 1; j <= n; ++j)
            {
   
                dp[i][j] = dp[i - 1][j] + dp[i][j -