【PTA】列出连通集 (25 分)——无向无权图邻接矩阵存储

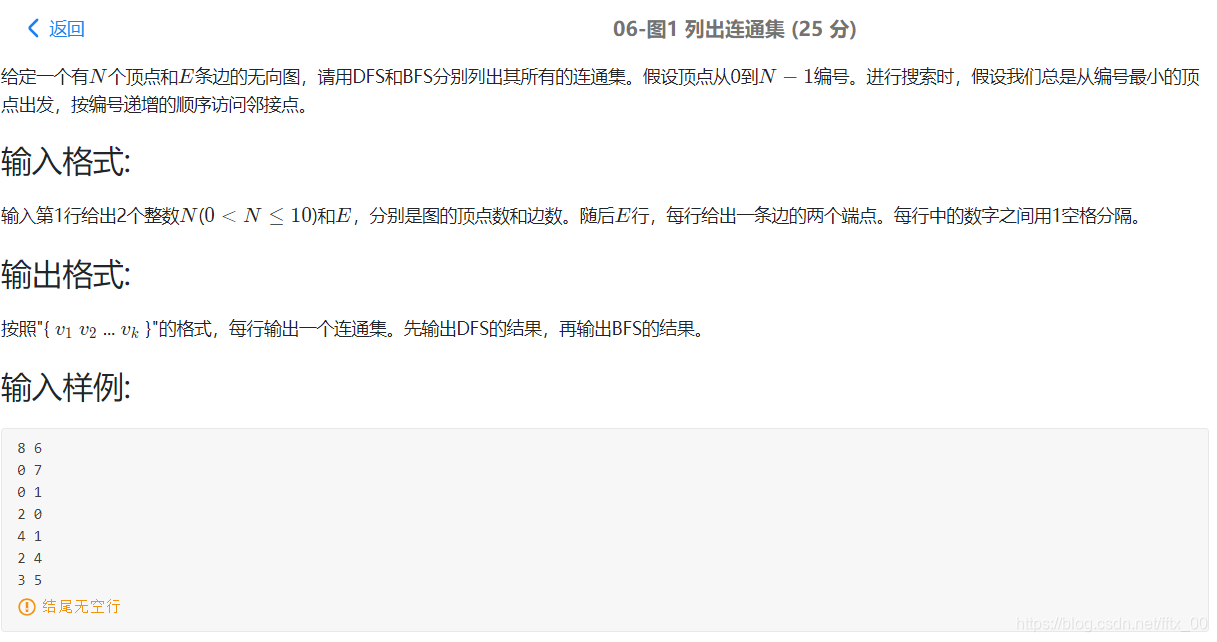
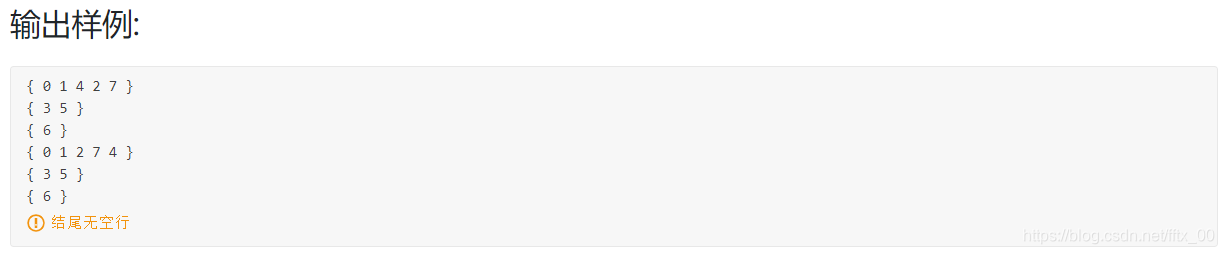
//因为要按编号递增顺序访问各邻接点，因此最好使用邻接矩阵存储
#include <iostream>
#include <algorithm>
#include <queue>
using namespace std;

//无向无权图：邻接矩阵、结点数、边数
#define MAXN 15
int G[MAXN][MAXN],Nv,Ne;

//读入图
void BuildGraph(){
  cin>>Nv>>Ne;

  int v1,v2;
  for(int i=0;i<Ne;i++){
    cin>>v1>>v2;
    G[v1][v2]=1;
    G[v2][v1]=1;
  }

}

//DFS
int visited[MAXN];
void DFS(int v){
  visited[v]=1;
  cout<<" "<<v;
  for(int j=0;j<Nv;j++){
    if(G[v][j] == 1 && visited[j] == 0){
      DFS(j);
    }
  }
}


//BFS
void BFS(int v){
  queue<int> q;
  q.push(v);
  visited[v]=1;
  int tmp;
  while(!q.empty()){
    tmp=q.front();
    cout<<" "<<tmp;
    q.pop();
    for(int i=0;i<Nv;i++){
      if(G[tmp][i] == 1 && visited[i] == 0){
        q.push(i);
        visited[i]=1;
      }
    }
  }

}

//因为不是连通图所以需要遍历结点，访问各结点的所有邻接点，从而遍历全图

//所有组DFS输出
void ListComponents_DFS(){
  for(int i=0;i<Nv;i++){
  if(!visited[i]){
    cout<<"{";
    DFS(i);
    cout<<" }\n";
  }
  }
}

//所有组BFS输出
void ListComponents_BFS(){
  for(int i=0;i<Nv;i++){
  if(!visited[i]){
    cout<<"{";
    BFS(i);
    cout<<" }\n";
  }
  }
}

int main(){
  BuildGraph();
  ListComponents_DFS();

//visited数组归零
  fill(visited,visited+Nv,0);

  ListComponents_BFS();

  return 0;
}