源哥每日一题第三弹 分解质因子中的 Pollard Rho和Miller Rabin算法（没写完，明天接着写）

想这个题纯属是突发奇想，想起了某个同行交友群的入群问题：找到某个数的质因子。推广一下，这个问题，就是将一个数拆成这样的形式：x = p1^a1*p2^a2*p3^a3……其中，pi为质数，这也就是传说中的唯一分解定理。

作为入群问题，自然是比较简单，莽的话一会就能跑出来，无聊的用用素数筛，但这些，毕竟都不是最为优美的算法——即使它的复杂度已经达到了普遍都可以接受的o（n）级别。

可不可以更快呢？答案当然是肯定的，不过我要说，接下来我所写的东西，和平时咱们学的算法不同，它不是一个百分之百准确的东西，但是却可以快速的解决这个问题。

现在 ，我要介绍：Pollard Rho分解因数算法

引入：想一个问题：在上学的时候，我们会经历一个神奇的现象：一个班中，总会有两个人的生日相同；为什么呢？

这个问题被称之为生日悖论：只要人数大于23 时， 这些人中出现相同生日的概率大于50%。

怎么会有这么神奇的事情呢？概率论给了我们完美的理论支撑：n个人中，每个人的生日不相同的概率为：

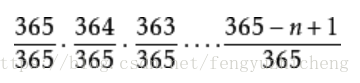
可以用算一下，当n等于23时就非常接近0.5了；当n大于60时，就已经小于0.01了；等于100时，无限接近0。

发生了一个比较有意思的事情：我们知道，只有人数在大于等于365（或366）的时候，我们才可以说，这个值是等于0的；

但其实，在大于100的时候，准确率就已经很高了，算到这里，就可以当作100%准确了。

回到一开始的问题。如何利用生日悖论分解n呢？

现在我们先假设，判断一个数是否是素数的次数为T；