图的遍历之最小生成树（Java实现）

    最小生成树是图理论中的一种最常见的应用，他是用最小的边连接所有的顶点。他们之间用最少量的边保证了他们彼此联通，这就组成了最下生成树。对于给定的顶点和边，可能有多种最小生成树，最小生成树边E的数量总比顶点V的数量小1，记住这个关系：E=V-1，这里不用关心边的长度，因为我们不是要找最短路径，而是要找最少数量的边。

    创建最下生成树的算法与搜索算法类似，可以使用深度优先搜索也可以使用广度优先搜索来实现，在搜索过程中，记录所走过的边，就可以创建一颗最小生成树。

     这里以下图为例，图中顶点和边之间因为多条边的缘故，连通性虽好，但是过于复杂，其实可以有更少的边组成更简洁的图。

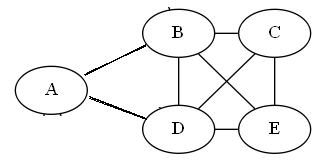
这里，如果只有如下的边，AB BC CD DE，也能让图联通起来，这就是这个图的一种最小生成树。如下图所示：

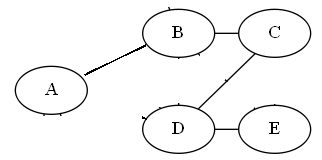
这时候边就是四条，顶点五个，正好满足E=V-1。下面给出最下生成树的实现代码：

Vertex.java

package com.xxx.algorithm.wh.mstgrapch;

public class Vertex {
	public char label;
	public boolean visited;
	public Vertex(char label){
		this.label = label;
		this.visited = false;
	}
}

StackX.java

package com.xxx.algorithm.wh.mstgrapch;

public class StackX {
	private final int SIZE=20;
	private int[] st;
	private int top;
	public StackX(){
		st = new int[SIZE];
		top = -1;
	}
	
	public void push(int i){
		st[++top] = i;
	}
	
	public int pop(){
		return st[top--];
	}
	
	public int peek(){
		return st[top];
	}
	
	public boolean isEmpty(){
		return top == -1;
	}
}

Graph.java

package com.xxx.algorithm.wh.mstgrapch;

public class Graph {
	
	private final int MAX_VERTS=20;
	private Vertex[] vertLists;
	private int[][] adjMat;
	private int nVerts;
	private StackX stack;
	
	public Graph(){
		vertLists = new Vertex[MAX_VERTS];
		adjMat = new int[MAX_VERTS][MAX_VERTS];
		nVerts = 0;
		for(int i=0;i<MAX_VERTS;i++){
			for(int j=0;j<MAX_VERTS;j++){
				adjMat[i][j] = 0;
			}
		}
		stack = new StackX();
	}

	public void addVertex(char label){
		vertLists[nVerts++] = new Vertex(label);
	}
	
	public void addEdge(int start,int end){
		adjMat[start][end] = 1;
		adjMat[end][start] = 1;
	}
	
	public void displayVertex(int v){
		System.out.print(vertLists[v].label);
	}
	
	public void mst(){
		stack.push(0);
		vertLists[0].visited = true;
		while(!stack.isEmpty()){
			int currentVertex = stack.peek();
			int v = getUnvisitedVertex(currentVertex);
			if(v==-1){
				stack.pop();
			}else{
				vertLists[v].visited = true;
				stack.push(v);
				displayVertex(currentVertex);
				displayVertex(v);
				System.out.print(" ");
			}
		}
		
		for(int i=0;i<nVerts;i++){
			vertLists[i].visited = false;
		}
	}
	
	public int getUnvisitedVertex(int v){
		for(int j=0;j<nVerts;j++){
			if(adjMat[v][j]==1 && vertLists[j].visited==false)
				return j;
		}
		return -1;
	}
	
	public static void main(String[] args) {
		Graph graph = new Graph();
		graph.addVertex('A');
		graph.addVertex('B');
		graph.addVertex('C');
		graph.addVertex('D');
		graph.addVertex('E');
		
		graph.addEdge(0,1);
		graph.addEdge(0,3);
		graph.addEdge(1,2);
		graph.addEdge(3,4);
		graph.addEdge(2,3);
		graph.addEdge(2,4);
		
		System.out.print("mst:");
		graph.mst();
		System.out.println();
	}

}

运行程序，打印信息如下：

mst:AB BC CD DE 

    最小生成树的算法与深度优先搜索的方法大部分重叠，其中最主要区别的就是遍历的时候，打印的是边的信息，而不是顶点信息。