二叉搜索树

前言

在之后我们需要介绍两个非常重要的结构，分别是Set和Map，而在介绍之前，我们需要先介绍一下二叉搜索树，为之后的学习做一个铺垫

---

一、概念

二叉搜索树：又称为二叉排序树，它可能是棵空树，也可能不是
存储方式一般采用链式存储，因为二叉搜索树不一定是一棵完全二叉树，那么采用顺序存储可能就会造成空间的浪费
二叉搜索树的结构遵循以下原则：
如果二叉搜索树不是空树，且根节点存在孩子节点

1.左子树所有节点的值一定比根节点的值小
2.右子树所有节点的值一定比根节点的值大
3.左子树的根节点和右子树的根节点也是一棵二叉搜索树
以上原则我们可以得知，二叉搜索树的中序遍历有序

二、操作

（一）查找

当我们要查找某一个值在二叉搜索树中是否存在时，那么我们需要从根节点开始查找，步骤：

1. 如果根节点的值大于目标值，那么向左遍历
2. 如果根节点的值小于目标值，那么向右遍历
3. 如果根节点的值等于目标值，return 节点

一直重复上述过程，如果遍历到null，那么表示二叉搜索树中没有目标值，return null
如下图：

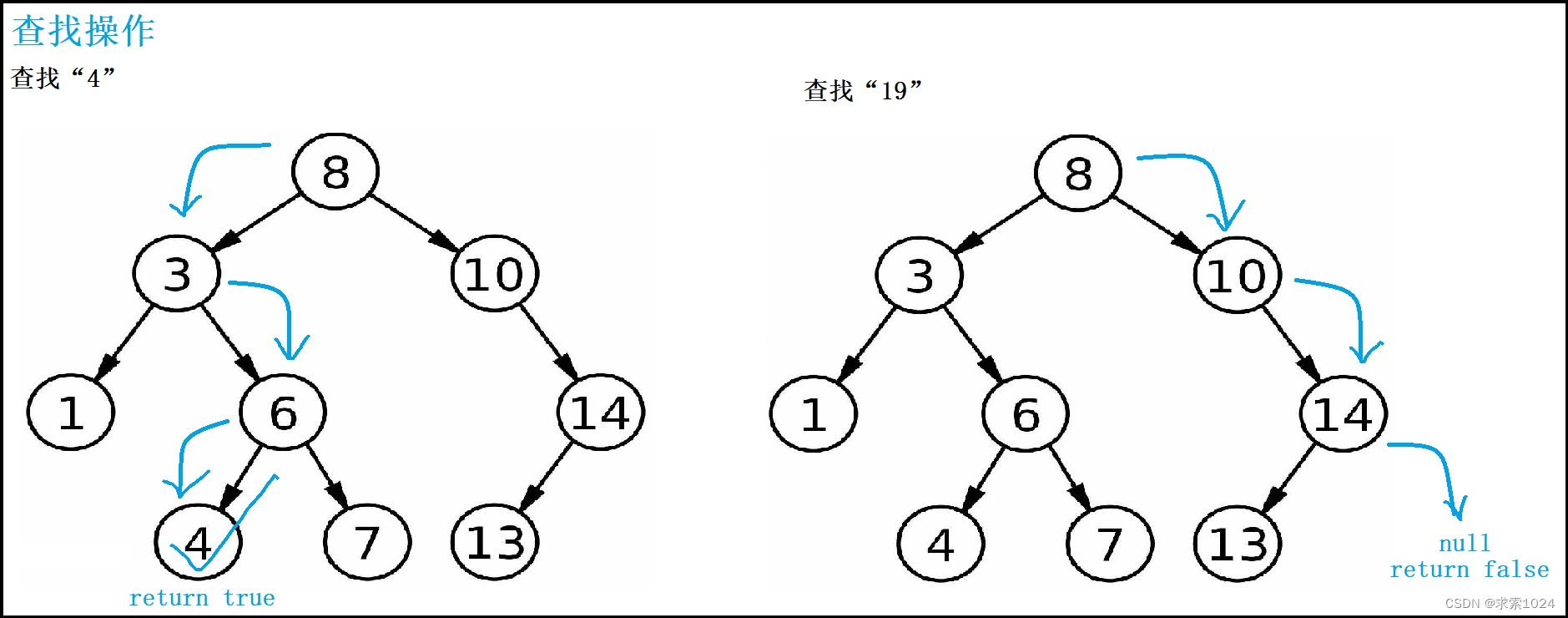
从上述查找过程我们可以看出二叉搜索树的查找和二分查找几乎一模一样，区别就在于二叉搜索树不一定是一棵完全二叉树，最坏情况下甚至是一棵单叉树，时间复杂度最坏情况达到了O(N)
代码示例：

/**
 * 非递归查找某个元素是否在本树中
 * 时间复杂度：O(N)（最坏情况下二叉搜索树是一棵单叉树）
 * 空间复杂度：O(1)
 * @param val
 * @return
 */
public TreeNode treeNodeSearch(int val) {
    TreeNode cur = root;
    while(cur != null) {
        if(cur.val == val) {
            return cur;
        }else if(cur.val > val) {
            cur = cur.left;
        }else {
            cur = cur.right;
        }
    }
    return null;
}

//递归查找，查找的树不一定是本树
public TreeNode treeNodeSearch(int val,TreeNode root) {
    if(root == null) {
        return null;
    }
    if(root.val == val) {
        return root;
    }else if(root.val > val){
        return treeNodeSearch(val,root.left);
    }else {
        return treeNodeSearch(val,root.right);
    }
}

（二）插入

前提说明：普通二叉搜索树的插入不考虑树的平衡问题

思路：我们的方法和查找类似，先找到要插入位置的双亲结点，然后进行插入，如果搜索树中本来就有这个元素，返回false

如下图：

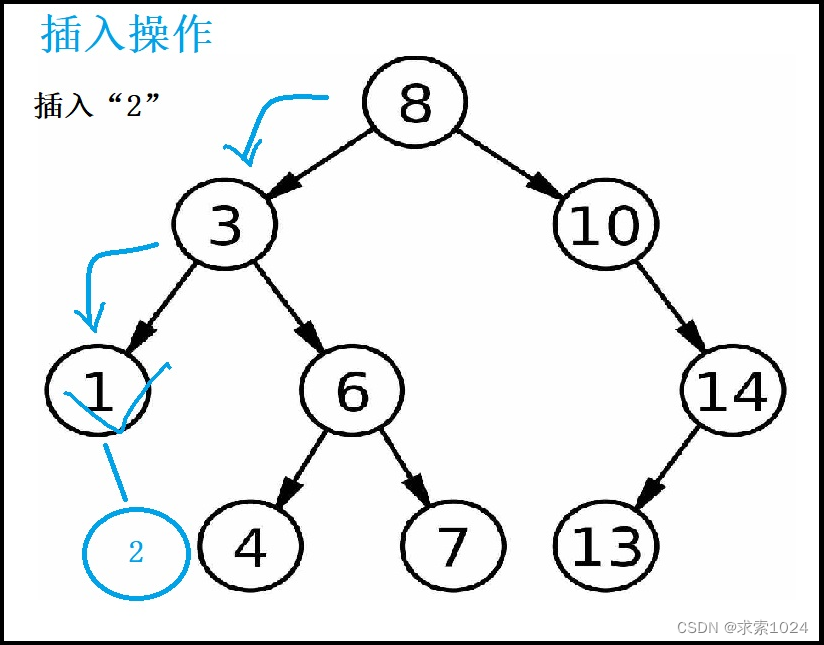
从上述插入过程中，我们知道如果根节点为null，那么我们插入到根节点的位置，否则都是在叶子节点进行插入

代码示例：

/**
 * 二叉搜索树的插入操作，不考虑树的平衡问题
 * 时间复杂度：O(N)
 * 空间复杂度：O(1)
 * @param val 需要插入的值
 * @return
 */
public boolean treeNodeInsert(int val) {
   if(root == null) {
       root = new TreeNode(val);
       return true;
   }
   TreeNode cur = root;
   while(cur != null) {
       if(cur.val > val) {
           if(cur.left == null) {
               cur.left = new TreeNode(val);
           }else {
               cur = cur.left;
           }
       }else if(cur.val < val){
           if(cur.right == null) {
               cur.right = new TreeNode(val);
           }else {
               cur = cur.right;
           }
       }else {
           return false;
       }
   }
   return true;
}

（三）删除（难点）

删除操作要比查找和插入操作复杂的多，需要考虑删除节点之后该由哪个节点顶替这个位置
那么根据上述问题，我们提出了四种情况解决思路：

1. cur.left == null && cur.right != null

• 当cur == root时，root = root.right
• 当cur != root时，如果parent.left == cur，那么parent.left = cur.right;如果parent.right == cur,那么parent.right == cur.right

2. cur.left != null && cur.right == null

• 当cur == root时，root = root.left
• 当cur != root时，如果parent.left == cur，那么parent.left = cur.left；如果parent.right == cur,那么parent.right = cur.left

3. cur.left != null && cur.right != null

（重点难点）
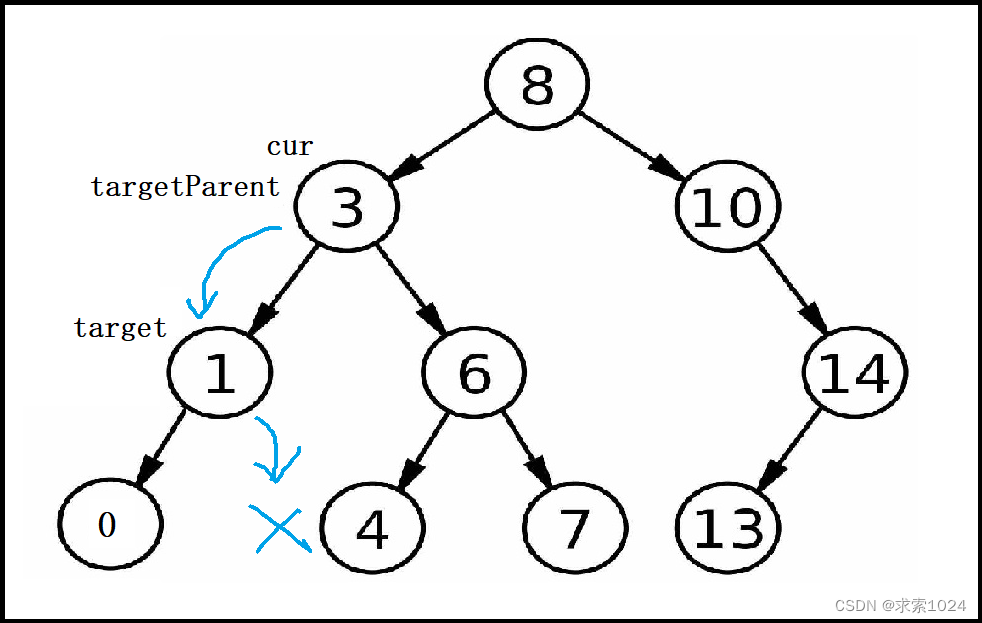
我们为了保证二叉搜索树的特性，那么就必须找到cur位置节点左子树的最大值或右子树的最小值，即左子树最右下角的节点或右子树最左下角的节点
下来我们以找左子树最右下角的节点为例：
此时我们选择再定义两个节点target = cur.left 与 targetParent = cur，target用来记录最右下角的节点，targetParent用来记录最右下角节点的双亲节点
当target.right == null时，cur.val = target.val。我们将cur的值更新之后，就要考虑删除target，而作为最右下角的节点，target一定没有右子树
易错易漏点:一般情况下我们可以直接将targetParent.right = target.left;可是如果targetParent = = cur，即下面这种情况下，那么我们就必须写成targetParent.left = target.left;

4. cur.left == null && cur.right == null

• 当cur == root时，root = null
• 当cur != root时，如果parent.left == cur,那么parent.left == null;如果parent.right == cur,那么parent.right == null

代码示例：

/**
 * 二叉搜索树的删除操作，不考虑树的平衡问题
 * 时间复杂度：O(N)
 * 空间复杂度：O(1)
 * @param val
 * @return
 */
public boolean treeNodeDelect(int val) {
    TreeNode cur = root;
    TreeNode parent = null;
    while(cur != null) {
        if(cur.val == val) {
            return removeNode(parent, cur);
        }else if(cur.val < val) {
            parent = cur;
            cur = cur.right;
        }else {
            parent = cur;
            cur = cur.left;
        }
    }
    return false;
}

private boolean removeNode(TreeNode parent, TreeNode cur) {
    if(cur.left == null && cur.right != null) {
        if(cur == root) {
            root = root.right;
            return true;
        }else {
            if(parent.left == cur) {
                parent.left = cur.right;
                return true;
            }else {
                parent.right = cur.right;
                return true;
            }
        }
    }else if(cur.left != null && cur.right == null){
        if(cur == root) {
            root = root.left;
            return true;
        }else {
            if(parent.left == cur) {
                parent.left = cur.left;
                return true;
            }else {
                parent.right = cur.left;
                return true;
            }
        }
    }else if(cur.left != null && cur.right != null) {
        TreeNode target = cur.left;
        TreeNode targetParent = cur;
        while(target.right != null) {
            targetParent = target;
            target = target.right;
        }
        cur.val = target.val;
        if(targetParent == cur) {
            targetParent.left = target.left;
        }else {
            targetParent.right = target.left;
        }
        return true;
    }else {
        if(cur == root) {
            root = null;
        }else if(parent.left == cur) {
            parent.left = null;
        }else {
            parent.right = null;
        }
        return true;
    }
}

三、整体实现

整体代码示例：

class BinarySearchTree {
    static class TreeNode {
        public int val;
        public TreeNode left;
        public TreeNode right;
        public TreeNode(int val) {
            this.val = val;
        }
    }

    public static TreeNode root = null;

    /**
     * 非递归查找某个元素是否在本树中
     * 时间复杂度：O(N)（最坏情况下二叉搜索树是一棵单叉树）
     * 空间复杂度：O(1)
     * @param val 需要查找的目标值
     * @return
     */
    public TreeNode treeNodeSearch(int val) {
        TreeNode cur = root;
        while(cur != null) {
            if(cur.val == val) {
                return cur;
            }else if(cur.val > val) {
                cur = cur.left;
            }else {
                cur = cur.right;
            }
        }
        return null;
    }

    //递归查找，查找的树不一定是本树
    public TreeNode treeNodeSearch(int val,TreeNode root) {
        if(root == null) {
            return null;
        }
        if(root.val == val) {
            return root;
        }else if(root.val > val){
            return treeNodeSearch(val,root.left);
        }else {
            return treeNodeSearch(val,root.right);
        }
    }

    /**
     * 二叉搜索树的插入操作，不考虑树的平衡问题
     * 时间复杂度：O(N)
     * 空间复杂度：O(1)
     * @param val 需要插入的值
     * @return
     */
    public boolean treeNodeInsert(int val) {
       if(root == null) {
           root = new TreeNode(val);
           return true;
       }
       TreeNode cur = root;
       while(cur != null) {
           if(cur.val > val) {
               if(cur.left == null) {
                   cur.left = new TreeNode(val);
               }else {
                   cur = cur.left;
               }
           }else if(cur.val < val){
               if(cur.right == null) {
                   cur.right = new TreeNode(val);
               }else {
                   cur = cur.right;
               }
           }else {
               return false;
           }
       }
       return true;
    }

    /**
     * 二叉搜索树的删除操作，不考虑树的平衡问题
     * 时间复杂度：O(N)
     * 空间复杂度：O(1)
     * @param val
     * @return
     */
    public boolean treeNodeDelect(int val) {
        TreeNode cur = root;
        TreeNode parent = null;
        while(cur != null) {
            if(cur.val == val) {
                return removeNode(parent, cur);
            }else if(cur.val < val) {
                parent = cur;
                cur = cur.right;
            }else {
                parent = cur;
                cur = cur.left;
            }
        }
        return false;
    }

    private boolean removeNode(TreeNode parent, TreeNode cur) {
        if(cur.left == null && cur.right != null) {
            if(cur == root) {
                root = root.right;
                return true;
            }else {
                if(parent.left == cur) {
                    parent.left = cur.right;
                    return true;
                }else {
                    parent.right = cur.right;
                    return true;
                }
            }
        }else if(cur.left != null && cur.right == null){
            if(cur == root) {
                root = root.left;
                return true;
            }else {
                if(parent.left == cur) {
                    parent.left = cur.left;
                    return true;
                }else {
                    parent.right = cur.left;
                    return true;
                }
            }
        }else if(cur.left != null && cur.right != null) {
            TreeNode target = cur.left;
            TreeNode targetParent = cur;
            while(target.right != null) {
                targetParent = target;
                target = target.right;
            }
            cur.val = target.val;
            if(targetParent == cur) {
                targetParent.left = target.left;
            }else {
                targetParent.right = target.left;
            }
            return true;
        }else {
            if(cur == root) {
                root = null;
            }else if(parent.left == cur) {
                parent.left = null;
            }else {
                parent.right = null;
            }
            return true;
        }
    }

    public void inorder(TreeNode root) {
        if(root == null) {
            return;
        }
        inorder(root.left);
        System.out.print(root.val + " ");
        inorder(root.right);
    }
}

四、性能分析

从上述增删查操作我们可以看到，无论哪一种都需要进行查找，因此查找的效率代表了二叉搜索树其他操作的效率
数组中的数都相同，但数的顺序不同，插入时就可能出现不同结构的二叉搜索树，可能是一棵完全二叉树，也有可能是一棵单支树

在完全二叉树的情况下，查询的效率可以达到O(logN)
而在单支树的情况下，查询效率就只有O(N)

如果结构变成单支树，那么二叉搜索树的性能就失去了，而对二叉搜索树采取优化，让它插入数据或者删除数据后，仍能保持一棵左右子树最大高度差不超过1的树，我们以后再讨论

五、与Java数据结构中类集的关系

TreeSet和TreeMap中的底层就是采取二叉搜索树的结构实现的，只不过是经过优化的二叉搜索树，又称为红黑树，而红黑树就是一棵近似平衡的二叉搜索树，红黑树不在这里进行过多介绍了