前言
小白跟随尚硅谷学习数据结构与算法的第四天—排序。
冒泡排序
一、基本介绍
冒泡排序(Bubble Sorting)的基本思想是:通过对待排序序列从前向后(从下标较小的元素开始),依次比较相邻元素的值,若发现逆序则交换,使值较大的元素逐渐从前移向后部,就像水底下的气泡一样逐渐向上冒。
二、冒泡排序的应用实例
我们举一个具体的案例来说明冒泡法。我们将五个无序的数:3,9,-1,10,20,使用冒泡排序法将其排成一个从小到大的有序数列。

冒泡排序小结
- 一共进行数组的大小-1次大小的循环 ;
- 每一趟排序的次数在逐渐减少;
- 优化方案:因为排序的过程中,各元素不断接近自己的位置,如果一趟比较下来没有进行过交换,就说明序列有序,可以提前结束冒泡排序,因此要在排序过程中设置个标志fag判断元素是否进行过交换,即优化。
三、代码实现:
public class BubbleSort {
public static void main(String[] args) {
int[] arr=new int[]{3,9,-1,10,20};
System.out.println("原始的数组:"+Arrays.toString(arr));
bubbleSort(arr);
}
public static void bubbleSort(int[] arr){
int temp;//临时变量记录数据
for (int i = 0; i <arr.length-1 ; i++) {// 控制排序次数
for (int j = 0; j < arr.length-1 ; j++) {
temp=arr[j];
//如果前面的数比后面的数大,则交换
if (arr[j]>arr[j+1]){
arr[j]=arr[j+1];
arr[j+1]=temp;
}
}
}
System.out.println("排序后的数组:"+Arrays.toString(arr));
}
}但是用该代码运行的排列存在一个问题,就是如果一趟比较下来没有进行过交换,该程序不会停止,而是执行for循环直至执行(数组的大小-1)次,当数据量较大时,极大地浪费了性能,因此我们在源代码上进行更改,使得当一趟比较下来没有进行过交换时,跳出循环。
public class BubbleSort2 {
public static void main(String[] args) {
int[] arr=new int[]{3,9,-1,10,20};
System.out.println(Arrays.toString(arr));
bubbleSort(arr);
}
//时间复杂度O(n^2)
public static void bubbleSort(int[] arr){
int temp;//临时变量
boolean flag=false;
for (int i = 0; i <arr.length-1 ; i++) {// 控制排序次数,例如
for (int j = 0; j < arr.length-1 ; j++) {
temp=arr[j];
//如果前面的数比后面的数大,则交换
if (arr[j]>arr[j+1]){
flag=true;
arr[j]=arr[j+1];
arr[j+1]=temp;
}
}
if (flag==false){//在一次排序中,一次交换都没有发生过
break;
}else {//重置flag
flag=false;
}
}
System.out.println(Arrays.toString(arr));
}
}在这里,我们加入了一个判断标识flag,初始flag=false,每一次进行数据交换,将flag=ture;在每一次循环结束后将flag重置为false,如果再一次循环中没有交换位置,则说明排序结束,这时候flag一直为false,我们加入一个判断条件,当flag==false时,跳出循环。
冒泡排序执行较慢,不推荐使用。
选择排序
一、基本介绍
选择式排序也属于内部排序法,是从欲排序的数据中,按指定的规则选出某元素,再依规定交换位置后达到排序的目的。
二、选择排序思想
选择排序(select sorting)也是一种简单的排序方法。它的基本思想是:第一次从arr[0]~arr[n-1]中选取最小值,与arr[0]交换,第二次从arr[1]~arr[n-1]中选取最小值,与arr[1]交换,第三次从arr[2]~arr[n-1]中选取最小值,与arr[2]交换,…,第i次从arr[i-1]~arr[n-1]中选取最小值,与arr[i-1]交换,…,第n-1次从arr[n-2]~arr[n-1]中选取最小值,与arr[n-2]交换,总共通过n-1次,得到一个按排序码从小到大排列的有序序列。
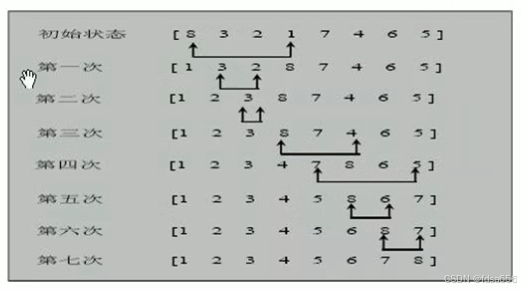
三、选择排序的思路图解

说明:
1.选择排序一共有数组大小-1轮排序;
2.每1轮排序,又是一个循环,循环的规则(代码);
2.1先假定当前这个数是最小数;
2.2然后和后面的每个数进行比较,如果发现有比当前数更小的数,就重新确定最小数,并得到下标;
2.3当遍历到数组的最后时,就得到本轮最小数和下标;
2.4 交换 [代码];
四、代码实现
public static void SelectSort2(int[] arr){
//第n次
for (int i = 0; i < arr.length-1 ; i++) {
int min=arr[i];
int minIndex=i;
for (int j = i; j <arr.length ; j++) {
if (arr[j]<min){ //说明假定的最小值并不是最小
min=arr[j]; //重置min
minIndex=j; //重置minIndex;
}
}
//将最小值,放在arr[0],即交换
arr[minIndex]=arr[i];
arr[i]=min;
}
System.out.println("排序过后:"+Arrays.toString(arr));
}插入排序
一、基本介绍
插入式排序属于内部排序法,是对于欲排序的元素以插入的方式找寻该元素的适当位置,以达到排序的目的。
二、插入排序法思想
插入排序(Insertionsorting)的基本思想是:把n个待排序的元素看成为一个有序表和一个无序表,开始时有序表中只包含一个元素,无序表中包含有n-1个元素,排序过程中每次从无序表中取出第一个元素,把它的排序码依次与有序表元素的排序码进行比较,将它插入到有序表中的适当位置,使之成为新的有序表。
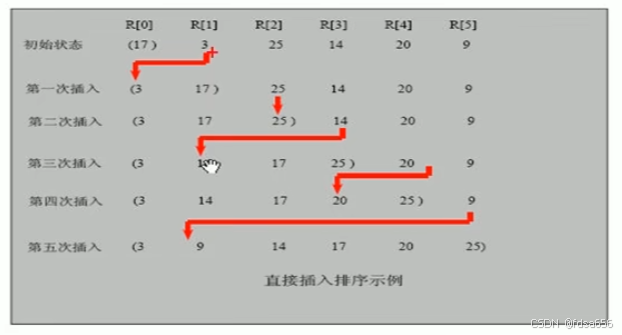
三、代码实现
public static void insertSort(int[] arr){
//定义待插入的数
for (int i = 1; i <arr.length ; i++) { //假设第一个数arr[0]是有序的,我们则要遍历后面的数,插入到arr[0]的有序表中
int temp= arr[i];//设置一个临时变量
int j;//用j表示有序数组中的数据
for (j = i-1; j >=0 ; j--) {//从i的前一位开始遍历,直至遍历结束
if (arr[j]>temp){//如果有序表中的元素大,则向后移一位
arr[j+1]=arr[j];
}else {
break;//如果有序表中的元素小,则退出循环
}
}
arr[j+1]=temp;
}
System.out.println(Arrays.toString(arr));
}总结:
老师给的代码有一些繁琐,根据自己的理解对源代码进行改善,在 arr[j + 1] = temp;这一步中,老师加了一个if (j + 1!=i)的判断,个人觉得没有必要,理论上加if判断可能是为了避免多余的赋值操作。但实际上,在标准的插入排序中,这种判断是多余的。
- 考虑以下情况:
- 当
temp比已排序部分的元素都大时,内层for循环会在j等于i - 1时就结束,此时j + 1等于i,添加if判断可以避免在这种情况下执行arr[j + 1] = temp;。 - 然而,在正常的插入排序中,即使执行
arr[j + 1] = temp;也不会导致错误,因为arr[j + 1]仍然是temp应该插入的位置。
- 当
希尔排序
一、插入排序问题分析
我们看简单的插入排序可能存在的问题.
数组 arr ={2,3,4,5,6,1}这时需要插入的数 1(最小),这样的过程是:
{2, 3, 4, 5,6, 6}
{2, 3, 4, 5, 5, 6}
{2, 3, 4, 4, 5, 6}
{2, 3, 3, 4, 5, 6}
{2, 2, 3, 4, 5, 6}
{1,2,3, 4, 5, 6}
结论:当需要插入的数是较小的数时,后移的次数明显增多,对效率有英雄。
二、基本介绍
希尔排序是希尔(DonaldShell)于1959年提出的一种排序算法。希尔排序也是一种插入排序,它是简单插入排序经过改进之后的一个更高效的版本,也称为缩小增量排序。
三、希尔排序基本思想
希尔排序是把记录按下标的一定增量分组,对每组使用直接插入排序算法排序;
随着增量逐渐减少,每组包含的关键词越来越多,当增量减至1时,整个文件恰
被分成一组,算法便终止
四、希尔排序的示意图
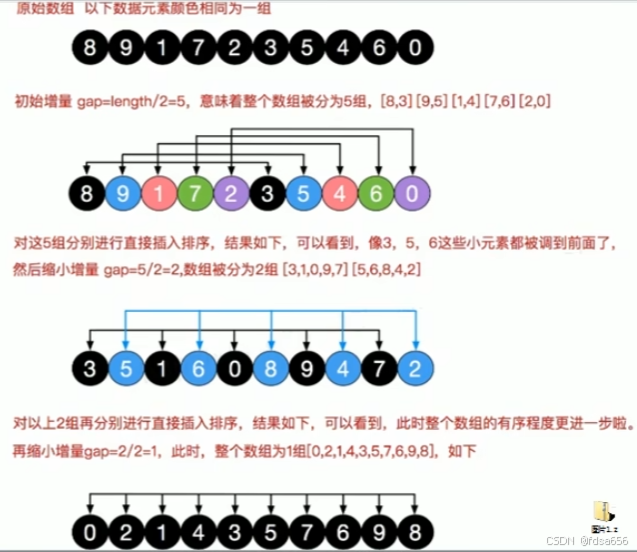

五、代码实现
public static void ShellSort(int[] arr){
//假定arr={8,0,1,7,2,3,9,4}
int gap=arr.length;//先确定间隔的长度 长度为8 则 间隔长度为8 4 2 1
while (gap>1){
gap=gap>> 1;//这里采用位运算 即除2 gap=4
for (int i = 0; i <arr.length-gap ; i++) {
int j;
int temp=arr[i+gap];//保存当前元素 arr[i + gap] 的值。
for (j =i; j >=0 ; j-=gap) {//从 i 开始,以 gap 为间隔向前比较元素。
if (arr[j]>temp){//如果当前元素 arr[j] 大于 temp,将 arr[j] 向后移动 gap 个位置(arr[j + gap] = arr[j];)
arr[j+gap]=arr[j];//将 temp 放入合适的位置。
}else {
break;
}
}
arr[j+gap]=temp;
}
}
System.out.println(Arrays.toString(arr));
}说明:
希尔排序的核心在于不断缩小间隔 gap,先对间隔为 gap 的元素组进行插入排序。
开始时,gap 较大,元素可以在数组中远距离移动,这有助于将较小的元素更快地移到数组的前部,较大的元素移到数组的后部,提高排序效率。
随着 gap 逐渐减小,最终 gap 会变为 1,此时就相当于普通的插入排序,但由于之前的预排序,数组已经部分有序,所以最终排序的效率比直接使用插入排序要高。
例如,对于输入数组 {8, 0, 1, 7, 2, 3, 9, 4}:
开始时,gap = 8,经过 gap = gap >> 1 后,gap = 4。
对于 gap = 4,会比较和交换 (8, 2)、(0, 3)、(1, 9)、(7, 4) 这些元素对,进行分组插入排序。
然后 gap 继续减半,直到 gap = 1,此时进行最后的微调,完成整个数组的排序。
希尔排序是一种不稳定的排序算法。这种算法利用了插入排序在处理部分有序数组时效率较高的特性,通过先对间隔元素进行排序,逐渐缩小间隔,最终完成整个数组的排序。
留言
创作不易,喜欢请点赞关注!谢谢!




















 1476
1476

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








