https://dspace.mit.edu/handle/1721.1/123142
这篇论文主要是讲多模配准的两个损失函数MI和MIND,网络结构还是voxelmorph。
摘要:
传统的方法还是优化方法(optimization,只要是DL的方法都会这么一说),所以很慢。
deep learning的方法是学习一个全局函数,加速配准过程。不过一般专注于单模配准。
引言:
不同的成像技术对体内组织有不同的反馈,所以才需要多模配准,来提供更多的信息。像MRI-T1可以区分脑部健康的组织,MRI-T2更容易反馈出一些高亮的异常结构,例如肿瘤。

图1.1 MRI-T1和MRI-T2同一个病人的脑部扫描。不同的组织对比,MRI-T1要比MRI-T2更好,最明显的是大脑皮层的轮廓。
多模配准之所以比单模配准更难,主要是因为两幅图像中对应结构的强度之间的复杂关系。比如一副图像中该组织结构是比较亮的,在另一个模态里可能就呈现出暗的。传统的方法在CPU上进行配准可能要十几分钟到一个小时不等(我接触到GPU上也就几分钟),一般都是优化问题,也就是最小化misalignment并且最大化形变场的smoothness。
论文着重对比两个损失函数mutual information(MI)和Modality-Independent Neighborhood Descriptor(MIND)。
背景:
2.1医学图像配准
最优化形变场:elastic registration、b-spline registration、discrete(non-differentiable)
2.2 基于学习的配准
基于学习的配准主要是学习一个全局的配准函数,大多数方法是监督学习,也就是需要ground truth deformations,gt很难获取。所以才有了无监督学习的方法,开创性的是voxelmorph

图2.1 voxelmorph encoder-decoder model结果,每个矩形表示3D volume,里面的数组表示channels,下面的数组表示空间分辨率。

图2.2 整体的模型图,voxelmorph学习一个变换 来事的moving image
来事的moving image 形变后与fixed image
形变后与fixed image 对齐,损失函数就是度量warped image
对齐,损失函数就是度量warped image 和fixed image
和fixed image 之间的相似性,并同时约束变换
之间的相似性,并同时约束变换 的光滑性。
的光滑性。
voxelMorph最小化的cost function:
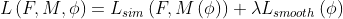 (2.1)
(2.1)
F和M就是两幅输入的图像, 是一个形变场,
是一个形变场, 是用来度量
是用来度量
 之间的相似性,
之间的相似性,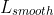 是deformation field 的正则项
是deformation field 的正则项 是正则项权重。
是正则项权重。 可以使mean squared error 或者是cross-correlation。
可以使mean squared error 或者是cross-correlation。
VoxelMorph配准速度也就GPU上一秒左右,CPU上1分钟左右,相同输入在CPU上可能就需要用小时做单位了(应该是夸张了),VoxelMorph训练的话就几天时间。单模配准上VoxelMorph已经很有效了,但是多模还没验证,主要是他的损失函数是mean-squared-error和cross-correlation,这两个损失函数也就是假设相应结构在两幅图像中是线性关系。
2.3 互信息Mutual Information
图像配准的方法都是最大化两幅图像的相似性。而相似性的度量,大多数是比较像素强度,比如L2 norm,L1 norm和cross correlation。单在多模配准中不能简单的假设两幅图像的强度关系是线性的。
一些传统的多模配准已经有一些方法,较为常见的比如mutual information(MI),一个经典的信息论方法,直观的定义了一个分布提供给另一个分布的信息量。
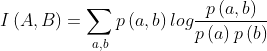 (2.2)
(2.2)
概率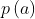 是在图像A中强度等于a的voxels比例,概率
是在图像A中强度等于a的voxels比例,概率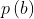 是在图像B中强度等于b的voxels比例。这两个概率可以通过为两幅图构造一个像素强度直方图来计算。
是在图像B中强度等于b的voxels比例。这两个概率可以通过为两幅图构造一个像素强度直方图来计算。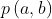 是两幅图像A和B的强度的联合分布,也就是两幅图像对应像素分别等于(a,b)的概率。等式2.2也就等于两个概率分布
是两幅图像A和B的强度的联合分布,也就是两幅图像对应像素分别等于(a,b)的概率。等式2.2也就等于两个概率分布和
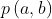 之间的Kullback-Leiber 散度,因此两幅图像最不相似,
之间的Kullback-Leiber 散度,因此两幅图像最不相似,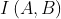 最大,由于
最大,由于表示两幅图像像素强度的分布是独立的,如果A和B对齐了,那么
和
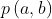 最接近,因为它最大限度地增加了一张图片与另一张图片之间的信息量。
最接近,因为它最大限度地增加了一张图片与另一张图片之间的信息量。
为了实现这个,我们对强度进行分箱bin intensities,然后离散的方式计算KL散度。
在多模图像配准中用负的互信息代替 ,因为最大化互信息来配准两幅图像,MI的实现可分成global mutual information和local mutal infromation分别对应image和patches的计算。互信息在传统配准中使用的比较多,但在基于学习的配准中使用的并不多。
,因为最大化互信息来配准两幅图像,MI的实现可分成global mutual information和local mutal infromation分别对应image和patches的计算。互信息在传统配准中使用的比较多,但在基于学习的配准中使用的并不多。
2.4 MIND
另外的一个loss function就是模态独立邻域描述子(Modality Independent Neighbourhood Descriptor,MIND),MIND是一个描述每个voxel周围局部模式的特征。这是通过观察中心patch和固定距离外的patch之间的相似性来计算的。基于MIND的相似函数背后的假设是,即使在不同的图像模态下,voxel周围的local patterns也应该是相似的,因此我们希望最小化我们所配准的两幅图像之间的MIND特征差异。
MIND由一个距离向量 和path size
和path size 来参数化,为了计算基于MIND的损失函数,我们希望看到6邻域patch与中心patch的相似性.
来参数化,为了计算基于MIND的损失函数,我们希望看到6邻域patch与中心patch的相似性.
图2.3 用于计算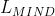 的6邻域patch视图,由参数 path size
的6邻域patch视图,由参数 path size 和distance
和distance  来参数化。
来参数化。
首先定义 来作为图像patches之间的相似性度量
来作为图像patches之间的相似性度量
 (2.3)
(2.3)
 是image,
是image, 和
和 是image中的两个locations,
是image中的两个locations, 是patch大小为
是patch大小为 的voxel到patch中心的位移集合。因此,
的voxel到patch中心的位移集合。因此, 计算以
计算以 和
和 为中心的两个图像patch之间的均方差,patch的大小为p×p×p。随后是MIND的定义
为中心的两个图像patch之间的均方差,patch的大小为p×p×p。随后是MIND的定义
(2.4)
 是image,
是image, 是image中的location,
是image中的location, 是distance vector。
是distance vector。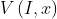 是local variance的评估。我们让MIND成为
是local variance的评估。我们让MIND成为 的一个Gaussian function,也就是当patches不相似低响应,相似是高响应。
的一个Gaussian function,也就是当patches不相似低响应,相似是高响应。
为了构建用于配准基于MIND的loss function,我们取我们希望对齐的两幅图像的MIND之间绝对差异的平均值:
 (2.5)
(2.5)
A B分别是fixed image 和wared image,R是长度为d的六个位移向量,在x,y,z方向各有两个。MIND在传统的图像配准中已经能够很好的使用了,但是在基于学习的配准方法中还没有比较好的运用。
方法
3.1 Mutual Information的可微性
如果要又在DL反向传播中,必须要可微分,每个体素应该连续地贡献到一个范围内的直方图容器中,而不是只贡献到它所处的容器中。我们使用Parzen windowing方法计算 ,给定一组n个样本
,给定一组n个样本 ,每个样本
,每个样本 贡献到
贡献到 与其距离函数
与其距离函数
(3.1).
我们将使用参数为 高斯函数作为权重函数W:
高斯函数作为权重函数W:
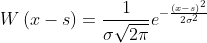 (3.2)
(3.2)
为了计算两幅图像A和B的MI,我们需要计算每幅图像的强度分布,以及两幅图像的联合分布。图像A 的强度分布是,为了计算联合分布将每个样本视为两幅图像中对应位置的一对强度:
(3.3)
为了利用(2.2)计算两幅图像的互信息,我们对k个等间距强度bin中心处的和
进行评估,
在所有
 对bin中心。参数k决定了每幅图像直方图中bin的数量,影响了这种互信息近似的准确性。
对bin中心。参数k决定了每幅图像直方图中bin的数量,影响了这种互信息近似的准确性。

图3.1 描述两幅图像A,B联合分布
图3.1 描述在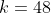 bins,两幅图像A,B联合分布
bins,两幅图像A,B联合分布 ,每个在热图中的(i,j)的square表示图像A的强度为i且图像B的强度为j的体素所占的比例,使用上面描述的Parzen窗口近似。左边描述的是还没有配准的两幅图像
,每个在热图中的(i,j)的square表示图像A的强度为i且图像B的强度为j的体素所占的比例,使用上面描述的Parzen窗口近似。左边描述的是还没有配准的两幅图像 分布,右边描述的是使用基于MI损失已经配准好的
分布,右边描述的是使用基于MI损失已经配准好的 分布。直观地看,配准后两幅图像的MI较大,因为热图上的亮点更集中,这意味着一幅图像的体素强度提供了另一幅图像对应体素强度的更多信息。
分布。直观地看,配准后两幅图像的MI较大,因为热图上的亮点更集中,这意味着一幅图像的体素强度提供了另一幅图像对应体素强度的更多信息。
Mutual information有两种global 和local。Global mutual information计算的是两幅图像的mutual information,local mutual information计算单是两幅图像对应patches的mutual information平均值。
global MI-base loss function:
 (3.4)
(3.4)
local MI-base loss function:
 (3.5)
(3.5)
 是patches的集合,之所以MI都是负的,因为两幅图对齐的时候MI最大,而一般loss都是最小化,所以加了一个负号。
是patches的集合,之所以MI都是负的,因为两幅图对齐的时候MI最大,而一般loss都是最小化,所以加了一个负号。
global MI是基于整个图像的强度分布。所以,假设两个体素具有相同的强度但在空间上彼此远离,global MI会把他们看做是一样的。为了让我们只考虑在空间上接近的体素,我们需要使用local MI来代替。因为local MI能够捕捉空间信息,我们直观地期望local MI表现得更好,但可能会以过拟合为代价。
3.2 Vectorized MI
要在VoxelMorph中使用global和local MI,必须以向量化vectorized的方式实现它们。向量化vectorized操作比循环操作运行速度快得多,而且由于每次通过网络的一对图像都必须计算MI损失,我们只能使用向量化操作来实现MI,否则体素形态将不能及时训练。
3.2.1 Vectorized Global MI
为了计算两幅图像A和B的global MI,我们首先计算矩阵和
,每个都有shape num_voxels×num_bins,表示每个体素对每个强度bin的贡献,如式(3.2)所示.这可以通过首先对图像进行重塑reshaping和tiling平铺,使其具有num_voxels×num_bin维数,减去bin中心的强度,然后进行element-wise操作来计算高斯函数。然后沿着0轴计算分布
 和
和 ,以及沿着0轴计算
,以及沿着0轴计算和
的均值。计算联合分布
 ,我们简化
,我们简化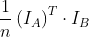 ,其中n是每张图像中的体素数,因为这将准确地给我们公式(3.3)中的总和。
,其中n是每张图像中的体素数,因为这将准确地给我们公式(3.3)中的总和。

算法1、global MI 的伪代码
3.2.2 Vectorized local MI
为了计算两幅图像A和B的局部MI,我们首先将每幅图像rehsape为大小为p×p×p的patch。然后我们进一步reshape得到数组 和
和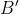 ,每个num_patch x p3大小,其中num_patch =
,每个num_patch x p3大小,其中num_patch =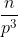 。注意,这个实现意味着patches不会重叠。为了得到重叠的patches,我们可以创建每个图像的多个副本,并重新reshape它们以创建offset patches,但为了节省内存,我们没有创建重叠的patches。一旦我们得到
。注意,这个实现意味着patches不会重叠。为了得到重叠的patches,我们可以创建每个图像的多个副本,并重新reshape它们以创建offset patches,但为了节省内存,我们没有创建重叠的patches。一旦我们得到 和
和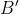 ,我们将第一个维度视为batch size,并继续进行与global MI相同的计算,只是现在所有的东西都是批处理的。
,我们将第一个维度视为batch size,并继续进行与global MI相同的计算,只是现在所有的东西都是批处理的。
3.3 Vectorized MIND
为了在VoxelmMrph中使用基于MIND的loss function,我们需要实现MIND向量化的方式。给定一幅图像A,MIND由一个高斯函数计算,该高斯函数是A的一个中心patch和它的六个固定距离的相邻patch中的一个之间的平均平方差。为了用向量化的方式来做这件事,我们首先在六个方向中的一个方向将图像A移动d个距离,然后减去原始图像A。然后取每个副本的元素平方,对patch大小p×p×p进行卷积,使kernel一致等于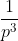 。这样得到的图像中,x位置的值是在所选方向上移动了d的patch与以x为中心的patch之间的平方差。为了计算均方差上的高斯函数,我们只需应用element0wise的操作,如squaring和dividing。为了计算基于MIND的loss function,我们需要计算在六个方向上的每一个方向都计算MIND特征,然后计算两幅图像MIND的绝对差,在所有n个voxels和六个方向上取平均。
。这样得到的图像中,x位置的值是在所选方向上移动了d的patch与以x为中心的patch之间的平方差。为了计算均方差上的高斯函数,我们只需应用element0wise的操作,如squaring和dividing。为了计算基于MIND的loss function,我们需要计算在六个方向上的每一个方向都计算MIND特征,然后计算两幅图像MIND的绝对差,在所有n个voxels和六个方向上取平均。
实验:
41.数据集
14,000 MRI-T1 :ADNI, OASIS , ABIDE, ADHD200 , MCIC , PPMI, HABS, and Harvard GSP.
6000 train, 3000 validate, and 5000 test images
预处理仿射空间归一化,脑组织提取。利用FreeSurfer,在分割过程中,采用人工质量控制来捕获较大的误差
MRI-T2:ADNI
T1->T2 atlas
虽然我们的方法是无监督的,因此不需要分割,但我们使用分割精度作为一个代理来评估图像配准精度,因此我们需要对我们的T2 atlas进行分割,以评估我们的方法。T2扫描没有分割,但是所有的T1扫描都分割,所以我们取同一个病人的T1扫描并将其与T2扫描进行仿射配准。然后,我们用仿射变换warpT1扫描的segmentation ,得到T2扫描的segmentation。仿射关系通过ANTs-MI计算,使用传统的优化方法最大化MI来计算多模配准。由于两次扫描都来自同一对象,我们期望仿射配准会相当准确。因为我们没有T2 segmentations,所以没有办法对它进行评估,但是我们可以可视化resulting segmentation。从图4.1上看到脑室在T2上表现的非常好,并且海马体也覆盖的差不多。最后一步就是确保T2已经与所有的T1仿射对齐了,这样模型就变得比较容易训练。
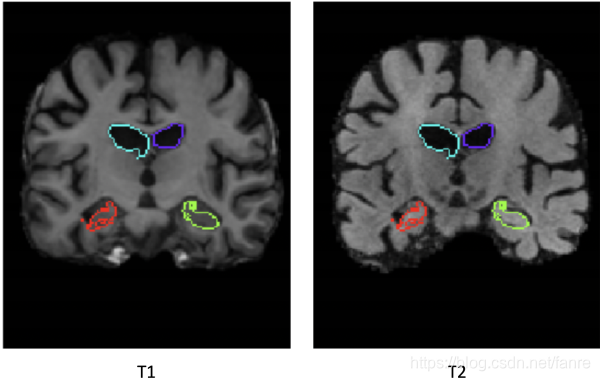
图4.1 左边:原始的T1扫描和风格,仿射变换到T2扫描。右侧:T2扫描覆盖T1变换的分割。上面两个是脑室,下面两个是海马体。
4.2 评价度量
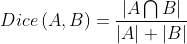
4.3 baseline
Symmetric Normalization (SyN) ,Advanced Normalization Tools (ANTs) software


























 1232
1232

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








