【MachineLearning】之 神经网络

一、前言

---

人工神经网络（英语：Artificial neural network，简称：ANN）

感知机模型就是一个人工神经网络，只不过是一个结构简单的单层神经网络。

当要解决线性不可分或者多分类问题，往往会尝试将多个感知机组合在一起，变成一个更复杂的神经网络结构。

1 层神经网络结构

2 层神经网络结构

二、概念

---

（1）什么是激活函数

逻辑回归、感知机、多层感知机与人工神经网络 4 个概念，这 4 种方法都与线性函数有关，而区别在于对线性函数的因变量的不同处理方式上面。

$$f(x)=w_1{x}_1+w_2{x}_2+\cdots +w_n{x}_n+b=WX+b\text{\hspace{1em}(1)}$$

• 对于逻辑回归而言，我们是采用了 $sigmoid$ 函数将 $f(x)$ 转换为概率，最终实现二分类。
• 对于感知机而言，我们是采用了 $sign$ 函数将 $f(x)$ 转换为 -1 和 +1 最终实现二分类。
• 对于多层感知机而言，具有多层神经网络结构，在 $f(x)$ 的处理方式上，一般会有更多的操作。

于是，$sigmoid$ 函数和 $sign$ 函数还有另外一个称谓，叫做「激活函数（Activation function）」

（2）激活函数的作用

作用：针对数据进行非线性变换，解决线性模型无法完成的分类任务

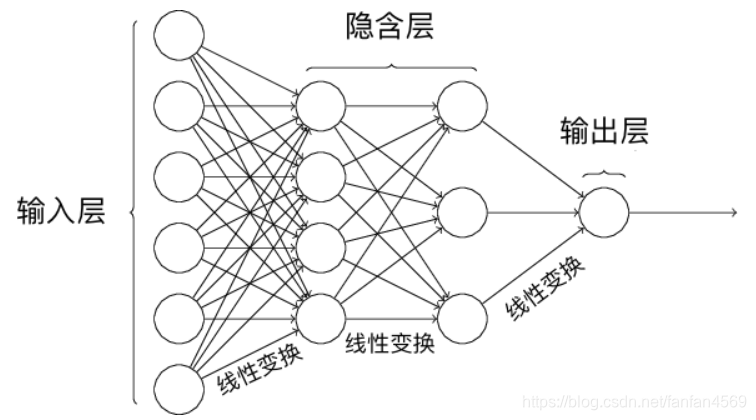
如上图所示，线性变换的多重组合依旧还是线性变换。如果我们在网络结构中加入激活函数，就相当于引入了非线性因素，这样就可以解决线性模型无法完成的分类任务。

（3）反向传播直观认识

组合成多层神经网络之后，更新权重的过程就变得复杂起来，而反向传播算法正是为了快速求解梯度而生。

参考资料：http://galaxy.agh.edu.pl/~vlsi/AI/backp_t_en/backprop.html

下图呈现了一个经典的 3 层神经网络结构，其包含有 2 个输入 $x_1$ 和 $x_2$ 以及 1 个输出 $y$。

网络中的每个紫色单元代表一个独立的神经元，它分别由两个单元组成。一个单元是权重和输入信号，而另一个则是上面提到的激活函数。其中，$e$ 代表激活信号，所以 $y=f(e)$ 就是被激活函数处理之后的非线性输出，也就是整个神经元的输出。

注：此处与下文使用g()作为激活函数稍有不同

下面开始训练神经网络，训练数据由输入信号 $x_1$ 和 $x_2$ 以及期望输出 $z$ 组成，首先计算第 1 个隐含层中第 1 个神经元 $y_1=f_1(e)$ 对应的值。

接下来，计算第 1 个隐含层中第 2 个神经元 $y_2=f_2(e)$ 对应的值。

然后是计算第 1 个隐含层中第 3 个神经元 $y_3=f_3(e)$ 对应的值。

与计算第 1 个隐含层的过程相似，我们可以计算第 2 个隐含层的数值。

最后，得到输出层的结果：

上面这个过程被称为前向传播过程，那什么是反向传播呢？接着来看：

当我们得到输出结果 $y$ 时，可以与期望输出 $z$ 对比得到误差 $\delta$。

然后，我们将计算得到的误差 $\delta$ 沿着神经元回路反向传递到前 1 个隐含层，而每个神经元对应的误差为传递过来的误差乘以权重。

同理，我们将第 2 个隐含层的误差继续向第 1 个隐含层反向传递。

此时，我们就可以利用反向传递过来的误差对从输入层到第 1 个隐含层之间的权值 $w$ 进行更新，如下图所示：

同样，对第 1 个隐含层与第 2 个隐含层之间的权值 $w$ 进行更新，如下图所示：

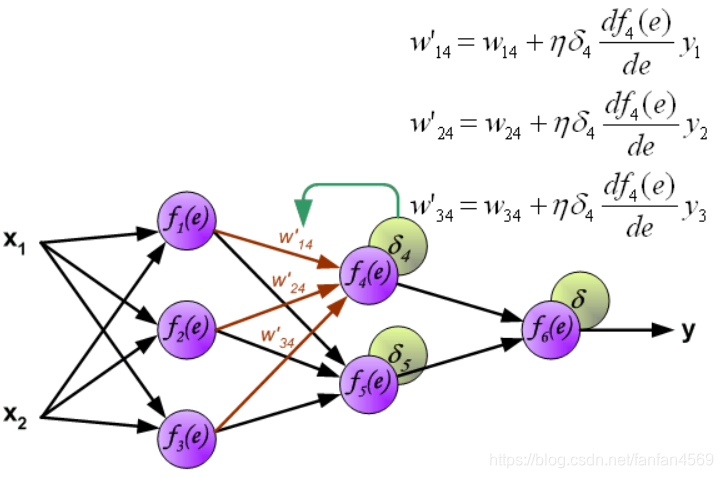
最后，更新第 2 个隐含层与输出层之间的权值 $w$ ，如下图所示：

图中的 $\eta$ 表示学习速率。这就完成了一个迭代过程。更新完权重之后，又开始下一轮的前向传播得到输出，再反向传播误差更新权重，依次迭代下去。

所以，反向传播其实代表的是反向传播误差。

三、实战

---

（1）定义神经网络结构

构建包含 1 个隐含层的人工神经网络结构。其中，输入层为 2 个神经元，隐含层为 3 个神经元，并通过输出层实现 2 分类问题的求解。该神经网络的结构如下：

本次实验中，激活函数为 $sigmoid$ 函数：
$$sigmoid(x)=\frac{1}{1+e^{-x}}\text{\hspace{1em}(2a)}$$

由于下面要使用 $sigmoid$ 函数的导数，所以同样将其导数公式写出来：

$$\Delta sigmoid(x)=sigmoid(x)(1-sigmoid(x))\text{\hspace{1em}(2b)}$$

python 实现

# sigmoid 函数
def sigmoid(x):
    return 1 / (1 + np.exp(-x))

# sigmoid 函数求导
def sigmoid_derivative(x):
    return sigmoid(x) * (1 - sigmoid(x))

（2） 前向传播

前向（正向）传播中，每一个神经元的计算流程为：线性变换 → 激活函数→输出值。

同时，约定：

• $Z$ 表示隐含层输出，$Y$ 则为输出层最终输出。
• $w_{ij}$ 表示从第 $i$ 层的第 $j$ 个权重。

于是，上图中的前向传播的代数计算过程如下。

神经网络的输入 $X$，第一层权重 $W_1$，第二层权重 $W_2$。为了演示方便，$X$ 为单样本，因为是矩阵运算，我们很容易就能扩充为多样本输入。

$$X=\left[\begin{array}{cc}{x}_1& x_2\end{array}\right]\text{\hspace{1em}(3)}$$

$$W_1=\left[\begin{array}{ccc}{w}_{11}& w_{12}& w_{13}\\ w_{14}& w_{15}& w_{16}\end{array}\right]\text{\hspace{1em}(4)}$$

$$W_2=\left[\begin{array}{c}{w}_{21}\\ w_{22}\\ w_{23}\end{array}\right]\text{\hspace{1em}(5)}$$

接下来，计算隐含层神经元输出 $Z$（线性变换 → 激活函数）。同样，为了使计算过程足够清晰，我们这里将截距项表示为 0。

$$Z=sigmoid(X\cdot W_1)\text{\hspace{1em}(6)}$$

最后，计算输出层 $Y$（线性变换 → 激活函数）：

$$Y=sigmoid(Z\cdot W_2)\text{\hspace{1em}(7)}$$

下面实现前向传播计算过程，将上面的公式转化为代码如下：

# 示例样本
X = np.array([[1, 1]])
y = np.array([[1]])

X, y

然后，随机初始化隐含层权重。

W1 = np.random.rand(2, 3)
W2 = np.random.rand(3, 1)

W1, W2

前向传播的过程实现基于公式（5）和公式（6）完成。

input_layer = X # 输入层
hidden_layer = sigmoid(np.dot(input_layer, W1)) # 隐含层，公式 20
output_layer = sigmoid(np.dot(hidden_layer, W2)) # 输出层，公式 22

output_layer

（3） 反向传播

接下来，我们使用梯度下降法的方式来优化神经网络的参数。那么首先需要定义损失函数，然后计算损失函数关于神经网络中各层的权重的偏导数（梯度）。

此时，设神经网络的输出值为 Y，真实值为 y。然后，定义平方损失函数如下：

$$Loss(y,Y)=\sum (y-Y{)}^2\text{\hspace{1em}(8)}$$

接下来，求解梯度 $\frac{\partial Loss(y,Y)}{\partial W_2}$，需要使用链式求导法则：

$$\frac{\partial Loss(y,Y)}{\partial W_2}=\frac{\partial Loss(y,Y)}{\partial Y}\frac{\partial Y}{\partial W_2}\text{\hspace{1em}(9a)}$$

$$\frac{\partial Loss(y,Y)}{\partial W_2}=2(Y-y)\ast \Delta sigmoid(Z\cdot W_2)\cdot Z\text{\hspace{1em}(9b)}$$

同理，梯度 $\frac{\partial Loss(y,Y)}{\partial W_1}$ 得：

$$\frac{\partial Loss(y,Y)}{\partial W_1}=\frac{\partial Loss(y,Y)}{\partial Y}\frac{\partial Y}{\partial Z}\frac{\partial Z}{\partial W_1}\text{\hspace{1em}(10a)}$$

$$\frac{\partial Loss(y,Y)}{\partial W_1}=2(Y-y)\ast \Delta sigmoid(Z\cdot W_2)\cdot W_2\ast \Delta sigmoid(X\cdot W_1)\cdot X\text{\hspace{1em}(10b)}$$

其中，$\frac{\partial Y}{\partial W_2}$，$\frac{\partial Y}{\partial W_1}$ 分别通过公式（6）和（5）求得。接下来，我们基于公式对反向传播过程进行代码实现。

# 公式 9
d_W2 = np.dot(hidden_layer.T, (2 * (output_layer - y) * 
              sigmoid_derivative(np.dot(hidden_layer, W2))))

# 公式 10
d_W1 = np.dot(input_layer.T,  (
       np.dot(2 * (output_layer - y) * sigmoid_derivative(
       np.dot(hidden_layer, W2)), W2.T) * sigmoid_derivative(np.dot(input_layer, W1))))

d_W2, d_W1

现在，就可以设置学习率，并对 $W_1$, $W_2$ 进行一次更新了

# 梯度下降更新权重, 学习率为 0.05

W1 -= 0.05 * d_W1 # 如果上面是 y - output_layer，则改成 +=
W2 -= 0.05 * d_W2

W2, W1

以上，我们就实现了单个样本在神经网络中的 1 次前向 → 反向传递，并使用梯度下降完成 1 次权重更新。那么，下面我们完整实现该网络，并对多样本数据集进行学习。

# 示例神经网络完整实现
class NeuralNetwork:
    
    # 初始化参数
    def __init__(self, X, y, lr):
        self.input_layer = X
        self.W1 = np.random.rand(self.input_layer.shape[1], 3)
        self.W2 = np.random.rand(3, 1)
        self.y = y
        self.lr = lr
        self.output_layer = np.zeros(self.y.shape)
    
    # 前向传播
    def forward(self):
        self.hidden_layer = sigmoid(np.dot(self.input_layer, self.W1))
        self.output_layer = sigmoid(np.dot(self.hidden_layer, self.W2))
    
    # 反向传播
    def backward(self):
        d_W2 = np.dot(self.hidden_layer.T, (2 * (self.output_layer - self.y) *
                      sigmoid_derivative(np.dot(self.hidden_layer, self.W2))))
        
        d_W1 = np.dot(self.input_layer.T, (
               np.dot(2 * (self.output_layer - self.y) * sigmoid_derivative(
               np.dot(self.hidden_layer, self.W2)), self.W2.T) * sigmoid_derivative(
               np.dot(self.input_layer, self.W1))))
        
        # 参数更新
        self.W1 -= self.lr * d_W1
        self.W2 -= self.lr * d_W2

接下来，我们使用实验一开始的示例数据集测试，首先我们要对数据形状进行调整，以满足需要。

X = df[['X0','X1']].values # 输入值
y = df['Y'].values.reshape(len(X), -1) # 真实 y，处理成 [[],...,[]] 形状

接下来，我们将其输入到网络中，并迭代 100 次：

nn = NeuralNetwork(X, y, lr=0.001) # 定义模型
loss_list = [] # 存放损失数值变化

for i in range(100):
    nn.forward() # 前向传播
    nn.backward() # 反向传播
    loss = np.sum((y - nn.output_layer) ** 2) # 计算平方损失
    loss_list.append(loss)

print("final loss:", loss)
plt.plot(loss_list) # 绘制 loss 曲线变化图

可以看到，损失函数逐渐减小并接近收敛，变化曲线比感知机计算会平滑很多。不过，由于我们去掉了截距项，且网络结构太过简单，导致收敛情况并不理想。本实验重点再于搞清楚 BP 的中间过程，准确度和学习难度不可两全。另外，需要注意的是由于权重是随机初始化，多次运行的结果会不同。