numpy的一次小尝试：一元线性回归分析

后天就要考试了，这两天一直在复习数理统计，刚才做了一个线性回归的题，发现我的答案和书上的答案大相径庭，所以我决定写程序来看一看谁对谁错

然后，我错了，书上的答案是正确的：

import turtle
import numpy as np
from matplotlib import pyplot as plt
x=[19.83,20.24,21.2,23.85,24.47,25.08,28.47,35.2,35.74,39.77,41.3,42.2,45.87,47.83,29.28,29.76,33.93,49.13,56.46,57.55]
y=[2466,2501,2390,2450,2350,2396,2331,2203,2159,2137,2092,2082,2060,2025,2297,2285,2238,2040,1865,1857]
X=np.zeros(20)
Y=np.zeros(20)
X2=np.zeros(20)
Y2=np.zeros(20)
XY=np.zeros(20)
i=0
while i<20:
    X[i]=x[i]
    Y[i]=y[i]
    i+=1
X2=X*X
Y2=Y*Y
XY=X*Y
x_mean=X.mean()
y_mean=Y.mean()
x2_mean=X2.mean()
y2_mean=Y2.mean()
xy_mean=XY.mean()
belta=(xy_mean-(x_mean*y_mean))/(x2_mean-pow(x_mean,2))
alpha=y_mean-belta*x_mean
# print("y="+alpha+"+"+belta+"*x")
Z=np.zeros(20)
Z=alpha+belta*X
sigma=y2_mean-pow(y_mean,2)-pow(belta,2)*(x2_mean-pow(x_mean,2))
print("alpha:",alpha)
print("belta:",belta)
print("sigma:",sigma)
fig=plt.figure()
ax=fig.add_subplot(1,1,1)
ax.plot(x,y,'r*')
ax.plot(X,Z,'b-')
ax.set_xlabel("x")
ax.set_ylabel("y")
fig.show()
turtle.done()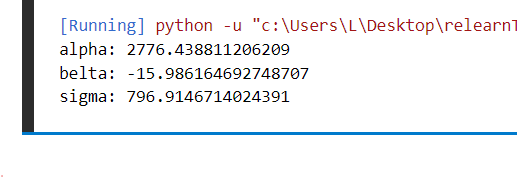

图一：计算参数输出

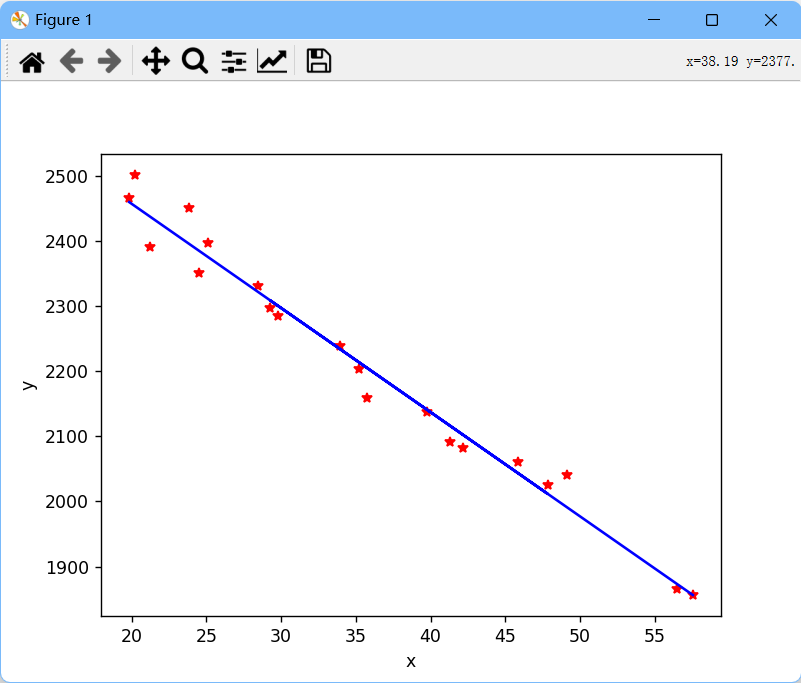
图二：回归直线图

想了半天，估计又是我敲计算器的时候算错了

然后嘛，第五题我也不想算了，就拿自己的程序运行一下，看看结果就好

改一下数据：

x=[2,4,6,8,10]
y=[64,138,205,285,360]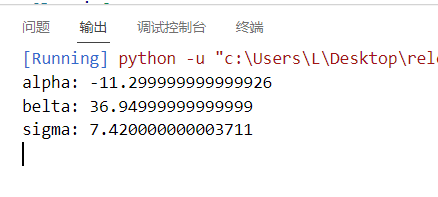

图三：计算所得参数

图四：回归直线

emm，看来我还是不细心，用计算器竟然都会按错。。。。。。

其实，我想，有时间的话，我想把数理统计这本书全部用程序写一遍，有时间再说吧。