思路:跟这题完全一样。点击打开链接 数据比HDU的强。
#include <cstdio>
#include <cstring>
#include <map>
#include <algorithm>
using namespace std;
struct S{
char op[5];
int x,id;
}e[100005];
bool cmpval(S a,S b)
{
if(a.x==b.x) return a.op[0]<b.op[0];
return a.x<b.x;
}
bool cmpid(S a,S b)
{
return a.id<b.id;
}
int n,cnt,val[100005],num[400005];
long long sum[400005][5];
void build(int idx,int s,int e)
{
if(s!=e)
{
int mid=(s+e)>>1;
build(idx<<1,s,mid);
build(idx<<1|1,mid+1,e);
}
num[idx]=0;
for(int i=0;i<5;i++) sum[idx][i]=0;
}
void update(int idx,int s,int e,int pos,int flag)
{
num[idx]+=flag;
if(s==e)
{
sum[idx][1]+=val[s]*flag;
return;
}
int mid=(s+e)>>1;
if(pos<=mid) update(idx<<1,s,mid,pos,flag);
else update(idx<<1|1,mid+1,e,pos,flag);
for(int i=0;i<5;i++) sum[idx][i]=sum[idx<<1][i]+sum[idx<<1|1][i-num[idx<<1]%5>=0?i-num[idx<<1]%5:i-num[idx<<1]%5+5];//更新对应区间内下标为模5等于i数的和
}
long long query(int idx,int s,int e,int mod)
{
return sum[idx<<1][mod]+sum[idx<<1|1][mod-num[idx<<1]%5>=0?mod-num[idx<<1]%5:mod-num[idx<<1]%5+5];
}
int main()
{
int i;
long long ans;
while(~scanf("%d",&n))
{
map<int,int>mp;//用于离散化过程中判重,有可能存在先add a,再del a,再 add a的情况
for(i=0;i<n;i++)
{
scanf("%s",e[i].op);
if(e[i].op[0]=='s') e[i].x=0;
else scanf("%d",&e[i].x);
e[i].id=i;
}
sort(e,e+n,cmpval);
cnt=1;
for(i=0;i<n;i++)//离散化
{
if(e[i].op[0]=='a')
{
if(!mp[e[i].x]) mp[e[i].x]=cnt++;
val[mp[e[i].x]]=e[i].x;
e[i].x=mp[e[i].x];
}
else if(e[i].op[0]=='d')
{
e[i].x=mp[e[i].x];
}
}
sort(e,e+n,cmpid);
cnt--;
if(!cnt)//特判
{
for(i=0;i<n;i++)
{
if(e[i].op[0]=='s')
{
printf("0\n");
}
}
continue;
}
build(1,1,cnt);
for(i=0;i<n;i++)
{
if(e[i].op[0]=='a') update(1,1,cnt,e[i].x,1);
else if(e[i].op[0]=='d') update(1,1,cnt,e[i].x,-1);
else printf("%I64d\n",query(1,1,n,3));
}
}
}







 本文介绍了一种高效算法来计算数组中任意k个元素的中位数之和,通过将数组划分为五元组并找到每个五元组的中位数,然后计算这些中位数的总和。该方法特别适用于现代图形卡的加速应用。此外,文章提供了一个输入输出示例,并解释了如何快速实现这个算法。
本文介绍了一种高效算法来计算数组中任意k个元素的中位数之和,通过将数组划分为五元组并找到每个五元组的中位数,然后计算这些中位数的总和。该方法特别适用于现代图形卡的加速应用。此外,文章提供了一个输入输出示例,并解释了如何快速实现这个算法。
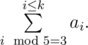
 operator stands for taking the remainder, that is
operator stands for taking the remainder, that is  stands for the remainder of dividing
stands for the remainder of dividing 















 448
448

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








