（2021-AAAI）Type-augmented Relation Prediction in Knowledge Graphs

（2021-AAAI）Type-augmented Relation Prediction in Knowledge Graphs

Keywords: Representation Learning

摘要

本文是关于知识图谱补全中的关系预测（relation prediction）。大多数现有的工作都是通过最大化观察到的三元组实例的可能性来进行补全，对实体类型信息、关系信息等本体信息的关注却不多。我们提出了一种类型增强的关系预测(TaRP)方法，其中我们将类型信息和实例级信息应用于关系预测。其中，类型信息和实例级信息分别编码为关系的先验概率和似然概率，并按照贝叶斯规则进行组合。在FB15K、FB15K-237、YAGO26K-906和DB111K-174四个基准数据集上，我们提出的TaRP方法的性能明显优于最先进的方法。此外，结果表明，该方法显著提高了数据效率。更重要的是，通过该模型，从特定数据集提取的类型信息可以很好地推广到其他数据集。

介绍

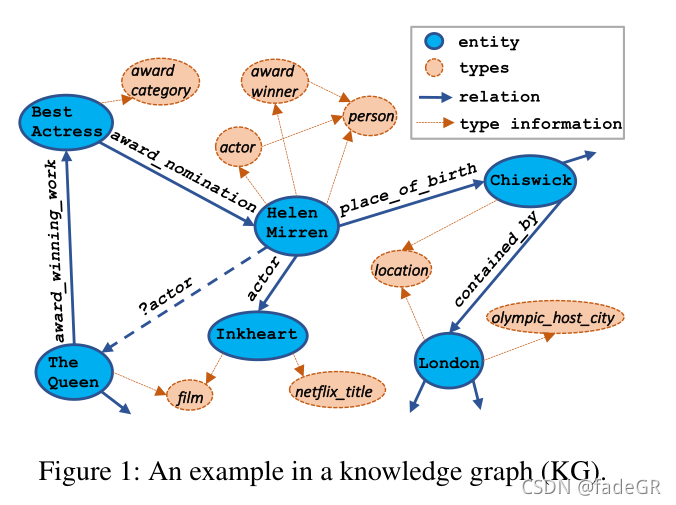
关系预测方法大都基于知识图谱嵌入，主要使用知识图谱中的两类信息进行分类：

• 实例级信息（Instance-level information） 也就是三元组信息
  • 例如：Helen_Mirren →place_of_birth → Chis_wick
• 本体信息（Ontological information） 也就是实体属性信息 type information
  • Helen_Mirren的类型{actor, award_winner, person}

大多数现有方法仅使用实例级信息来学习嵌入，而其他一些模型同时使用实例级信息和本体信息。类型信息例如本体信息可以直观地帮助关系预测，因为大多数关系可以将两种不同类型的实体连接为领域和范围。例如：

• 关系place_of_birth总是将person类型的实体和location类型的实体连接起来构成三元组。将此类类型信息集成到实例级训练三元组中可以使关系预测任务受益，特别是在缺乏足够的训练数据来学习嵌入的情况下。

如今一些现有的基于嵌入的模型集成了类型信息，但是这类模型通过模型训练来集成本体信息，来更好的地学习嵌入，因此容易出现以下缺点：

• 类型信息与层次信息没有显式区分，联合考虑两种信息来学习一组单一的模型参数
• 类型信息被紧密地编码到目标函数中，使得集成高度依赖于训练过程，因此在增加新的嵌入技术时不太灵活。我们将这种集成过程称为特性级集成（feature-level integration）。相反，我们提出了一种有效的决策级集成（decision-level integration）：给定类型信息和实例级信息分别编码为先验概率和可能性，所提出的决策级集成遵循贝叶斯规则将这两种信息结合起来。

在本文中，我们提出了一个简单而有效的框架，以增强现有的基于嵌入的模型与类型信息。我们工作的贡献如下:

• 所提出的决策级集成框架独立于基于嵌入的模型，可以灵活地应用于不同的基于嵌入的模型，无需额外的训练
• 在三个基准数据集上，所提出的类型增强关系预测(TaRP)方法比最先进的模型实现了更好的关系预测性能。此外，我们还表明，通过集成类型信息，TaRP对培训数据的依赖性更小，因此数据效率更高。
• 我们通过经验证明，从特定数据中提取的类型信息可以通过TaRP模型对其他不同的数据集进行一般化。

相关工作

介绍了现有知识图谱补全大多数基于嵌入的方法，同时简单介绍了基于嵌入的方法的基本内容：设计嵌入方式、设计评分函数与损失函数。都是基于TransE的思想不断演化更新，这些方法只是借用了实例级信息，并没有借助本体信息。

再讨论了现有的基于嵌入的方法而且结合了本体信息，也有很多，而且还探讨了本体信息中除了类型信息之外的信息利用情况。但他们都是将本体信息集成到特征级的实例信息，来更好的学习嵌入。

除了基于嵌入的方法还有基于路径的方法，但计算量大本文不讨论该情况。

TaRP: Type-augmented

Relation Prediction Model（关系预测模型）

在本节中，我们将介绍我们的类型增强关系预测(type-augmented relation prediction framework)（TaRP）框架，该框架使用来自知识图谱的类型信息增强现有的嵌入模型。我们的框架由两个组件组成:

• (a)先验模型，其中我们将类型信息编码为先验概率，详见章节;
• (b)基于现有实例级信息的似然模型。任何现有的基于嵌入的模型都可以作为似然模型，在本节中我们简要描述了三种用于实验的基于嵌入的模型。该框架使用贝叶斯规则集成了先验和似然模型的信息(详见本节)。

Type Information Integration （类型信息集成）

本节介绍将类型信息编码为先验概率的方法，定义知识图谱G={E,R,T}\mathcal{G}=\{\mathcal{E}, \mathcal{R}, \mathcal{T}\}G={E,R,T}，$\mathcal{E},\mathcal{R},\mathcal{T}$分别为实体集，关系集，类型集。

基于层次结构的类型权重：类型是有层次结构的，一个个包含关系，例如{person，actor…}，对于不同层次的类型赋予不同的权重。$H=/t_1/t_2/\dots ./t_k/\dots /t_K^1$就是一个不断具体化的类型。权重公式如下：
$$w_e^H\left(t_k\right)=\frac{\exp (k-1)}{{\sum }_{j=0}^{K-1}\exp (j)}$$
每一个实体都对应一个类型序列，在该类型序列中计算不同层次类型的权重。对于同一个实体中的同一个类型，取所有层次中的最小值$w_e(t)=$ $\min \left(w_e^{H_1}(t),w_e^{H_2}(t),\dots ,w_e^{H_N}(t)\right)$。例如：$H_1=/person/actor$ ，$H_2=/person/awar{d}_{w}inner$ ，$H_3=/person$ 所以计算得到： $w_e($ person $)=0.27,w_e($ actor $)=0.73$, $w_e($ award_winner $)=0.73$。同时类型分为头实体类型和尾实体类型：
$$\begin{array}{rl}{T}_{r,head}& ={\cup }_{e\in \mathrm{Head}(r)}{T}_e\\ T_{r,tail}& ={\cup }_{e\in \mathrm{Tail}(r)}{T}_e\end{array}$$

定义关系r的头实体集合：Head⁡(r)={eh∣(eh,r,et)∈G,∀et∈E}\operatorname{Head}(r)=\left\{e_{h} \mid\left(e_{h}, r, e_{t}\right) \in \mathcal{G}, \forall e_{t} \in \mathcal{E}\right\}Head(r)={eh​∣(eh​,r,et​)∈G,∀et​∈E}，定义关系r的尾实体集合：Tail⁡(r)={et∣(eh,r,et)∈G,∀eh∈E}\operatorname{Tail}(r)=\left\{e_{t} \mid\left(e_{h}, r, e_{t}\right) \in \mathcal{G}, \forall e_{h} \in \mathcal{E}\right\}Tail(r)={et​∣(eh​,r,et​)∈G,∀eh​∈E}，计算关系r对应头实体和尾实体的一个类型权重为：
$$\begin{array}{rl}{w}_{r,\text{ head }}(t)& =\sum _{e\in \mathrm{Head}(r)}{w}_e(t),\text{ for }t\in T_{r,head}\\ w_{r,tail}(t)& =\sum _{e\in \mathrm{Tail}(r)}{w}_e(t),\text{ for }t\in T_{r,tail}\end{array}$$

基于类型先验概率：计算头实体和关系的类型相似度，尾实体和关系的类型相似度，
$$\begin{array}{rl}& s\left(e_h,r\right)=\frac{{\sum }_{t\in T_{r,head}\cap T_{e_h}}{w}_{r,head}(t)}{{\sum }_{t\in T_{r,head}}{w}_{r,head}(t)}\\ & s\left(e_t,r\right)=\frac{{\sum }_{t\in T_{r,tail}\cap T_{e_t}}{w}_{r,tail}(t)}{{\sum }_{t\in T_{r,tail}}{w}_{r,tail}(t)}\end{array}$$
所以先验概率定义为：

$$p\left(r\mid \mathcal{T}\left(e_h,e_t,\mathcal{R}\right)\right)\triangleq \frac{s\left(e_h,r\right)s\left(e_t,r\right)}{{\sum }_{r^{\prime }\in \mathcal{R}}s\left(e_h,r^{\prime }\right)s\left(e_t,r^{\prime }\right)}$$
不同于以前的工作(Ma et al. 2017)，通过平等对待每种类型来衡量语义相似度。我们的基于类型的先验概率与基于层次的类型权重不仅编码类型信息，而且编码类型之间的底层层次。

为了消除噪声，引入$\eta$参数，公式如下：
$$w_{r,\ast }(t)\ge W_{r,\ast }^{\min }+\eta \times \left(W_{r,\ast }^{\max }-W_{r,\ast }^{min}\right)$$

嵌入基础模型

介绍常用的嵌入模型：

TransE： ${\mathbf{e}}_h,{\mathbf{e}}_r\in {\mathbb{R}}^d$ and $\mathbf{r}\in {\mathbb{R}}^d$.
$$f_r\left({\mathbf{e}}_h,{\mathbf{e}}_t\right)=-||{\mathbf{e}}_h\cdot \mathbf{r}-{\mathbf{e}}_t\Vert$$
RotatE： ${\mathbf{e}}_h,{\mathbf{e}}_r\in {\mathbb{C}}^d$ and $\mathbf{r}\in {\mathbb{C}}^d$.
$$f_r\left({\mathbf{e}}_h,{\mathbf{e}}_t\right)=-\Vert {\mathbf{e}}_h\circ \mathbf{r}-{\mathbf{e}}_t\Vert$$
QuatE： ${\mathbf{e}}_h,{\mathbf{e}}_r\in {\mathbb{H}}^d$ and $\mathbf{r}\in {\mathbb{H}}^d$.
$$f_r\left({\mathbf{e}}_h,{\mathbf{e}}_t\right)=-\Vert {\mathbf{e}}_h\otimes \frac{\mathbf{r}}{|\mathbf{r}|}-{\mathbf{e}}_t\Vert$$

以上的模型都只包含实例级信息，而不包含类型信息，所以要包含类型信息的话重新定义得分函数为：
$$p\left(e_h,e_t\mid r\right)\triangleq \exp \left(f_r\left({\mathbf{e}}_h,{\mathbf{e}}_t\right)\right)$$

类型信息集成

最后一步是将实例级信息与类型信息在决策级中集成。给定一个三元组$\left(e_h,r,e_t\right)$，根据类型信息$p\left(r\mid \mathcal{T}\left(e_h,e_t,\mathcal{R}\right)\right)$，我们得到关系的先验概率，同时得到实例级信息的模型$p\left(e_h,e_t\mid r\right)$，通过贝叶斯规则得到后验概率：

$$\begin{array}{rl}& p\left(r\mid e_h,e_t,\mathcal{T}\left(e_h,e_t,\mathcal{R}\right)\right)\\ & \propto p\left(e_h,e_t\mid r\right)p\left(r\mid \mathcal{T}\left(e_h,e_t,\mathcal{R}\right)\right)\end{array}$$
因此后验概率$p\left(r\mid e_h,e_t,\mathcal{T}\left(e_h,e_t,\mathcal{R}\right)\right)$既包含类型信息又包含实例级信息。我们提出的决策级集成独立于嵌入技术。与现有论文相比，这是显著的差异化因素，例如，(Ma et al. 2017;Xie, Liu, and Sun 2016)，将类型信息紧密地集成在特征级(集成在目标函数中)，使其不那么灵活地演化嵌入技术。

类型信息：$p\left(r\mid \mathcal{T}\left(e_h,e_t,\mathcal{R}\right)\right)$

实例信息：$p\left(e_h,e_t\mid r\right)$

最终概率：$p\left(r \mid e_{h}, e_{t}, \mathcal{T}\left(e_{h}, e_{t}, \mathcal{R}\right)\right) $

实验

为了评估我们的类型增强关系预测(TaRP)方法的表现，我们首先对现有模型进行消融研究;然后评估TaRP模型的表现。我们通过将TaRP模型与三个基于基线嵌入的模型(TransE、RotatE和QuatE)进行比较，来证明问题资产救援计划模型的有效性。此外，我们还表明，通过合并类型信息，TaRP比现有方法的数据效率高得多。此外，我们还演示了类型信息的泛化能力。在最后，我们的方法是先进的模型，同时应用了本体论信息。

数据集我们考虑了三个基准数据集用于关系预测任务:FB15K (Bordes et al. 2013)， Y AGO26K-906 (Hao et al. 2019)和DB111K-74 (Hao et al. 2019)。FB15K是一种流行的知识图谱补全的任务基准数据集，其类型信息已经被大多数之前的工作所使用，如(Ma et al. 2017;Guo et al. 2015;Xie, Liu, and Sun 2016)。Y AGO26K-906和DB111K-906是两个最新的包含显式本体信息的数据集，并没有被相关工作广泛考虑。FB15K由从FreeBase知识图中提取的三元组组成(Bollacker et al. 2008)。与(Xie, Liu, and Sun 2016)中介绍的FB15K类型信息相同。Y AGO26K-906和DB111K174都包含两种类型的KGs:实例KG和本体KG，它们通过类型链接相互连接。Y AGO26K-906和DB111K174的实例KGs分别由Y AGO知识图(Rebele et al. 2016)和DBpedia知识图(Lehmann et al. 2015)提取的三元组组成;并应用于关系预测任务。收集类型链接和本体KGs作为类型信息。三个数据集的统计信息如表1所示。

•FB15k-237（2013）：是知识图谱Freebase的子集，15k表示其中知识库中有15k个主题词，237表示共有237种关系

•YAGO26K-906 （2019）： 是知识图谱YAGO的子集， 26K表示其中知识库中有26K个主题词， 237表示共有237种关系

•DB111K-174 （2019）：是知识图谱DBpedia的子集， 111K表示其中知识库中有111K个主题词， 174表示共有174种关系

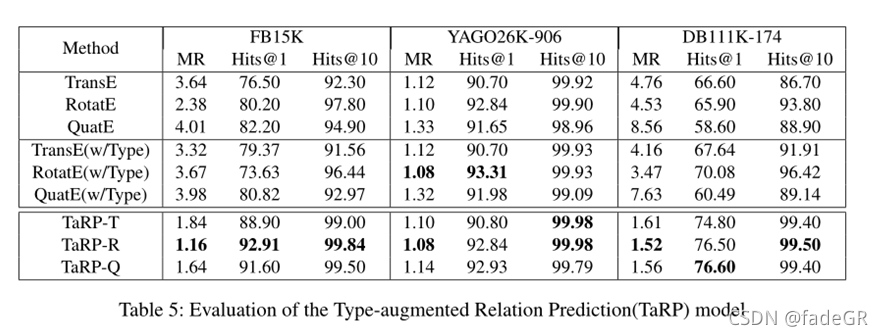
•结果表明，在不同的嵌入模型中引入类型信息，TaRP模型总能获得更好的性能

消融实验

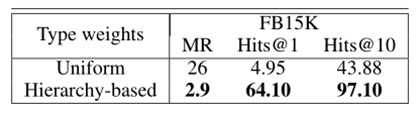
​ 基于层次的类型权重的有效性：

类型信息的有效性：

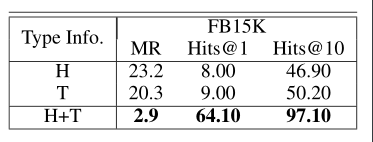
•H 仅头实体的类型信息

•T 仅尾实体的类型信息

•H+T头实体与尾实体的类型信息

TaRP模型评估

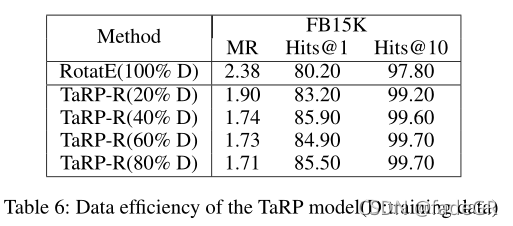
数据效率

•考虑从训练三元组的子集中学习嵌入

•结果表明，通过利用类型信息，TaRP对数据的依赖性更小，即数据效率更高

与SoTA模型对比

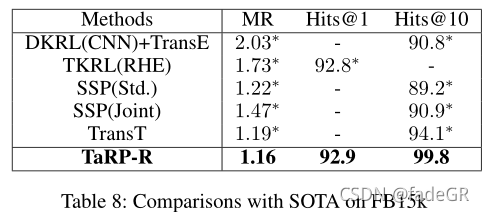
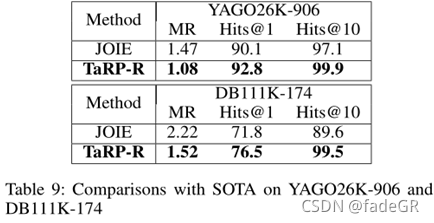
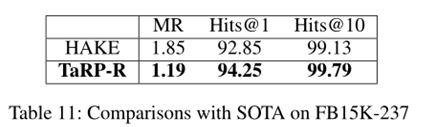
•DKRL (2016)、TKRL (2016)、SSP (2017)、TransT (2017)、JOIE（2019）

讨论

•提出决策级集成框架独立于基于嵌入的模型，可以应用于不同的基于嵌入的模型。

•提出的类型增强关系预测(TaRP)方法比最先进的模型实现了更好的关系预测性能。

•通过集成类型信息，TaRP对训练数据的依赖性更小，因此数据效率更高。

从特定数据中提取的类型信息可以通过TaRP模型对其他不同的数据集进行一般化

总结

在本文中，我们提出了一种有效的类型增广关系预测(TaRP)方法，该方法将类型信息和实例级信息应用于知识图谱的关系预测。将类型信息和实例级信息分别编码为关系的先验概率和可能性，并在决策级进行组合。我们的方法明显优于最先进的方法。此外，通过利用类型信息，TaRP模型能够比现有模型具有更高的数据效率。此外，从特定数据集提取的类型信息可以很好地推广到其他数据集。

•本文提出了一种有效的类型增强关系预测(TaRP)方法

•该方法将类型信息和实例级信息应用于知识图谱的关系预测

•将类型信息和实例级信息分别编码为关系的先验概率和可能性

•从特定数据集提取的类型信息可以很好地推广到其他数据集