解决评价类问题
不同指标权重和为1,同一指标不同方案和为1
| 指标权重 | 方案1 | 方案2 | … | |
|---|---|---|---|---|
| 指标1 | ||||
| 指标2 | ||||
| 指标3 | ||||
| … |
解决评价类问题的三个问题:
- 评价目标是什么?
- 为了达到目标有哪几种可选方案?
- 评价的准则或指标是什么?(根据什么来评价好坏)
优先选择知网(万方、百度学术、谷歌学术等平台)搜索相关文献 虫部落

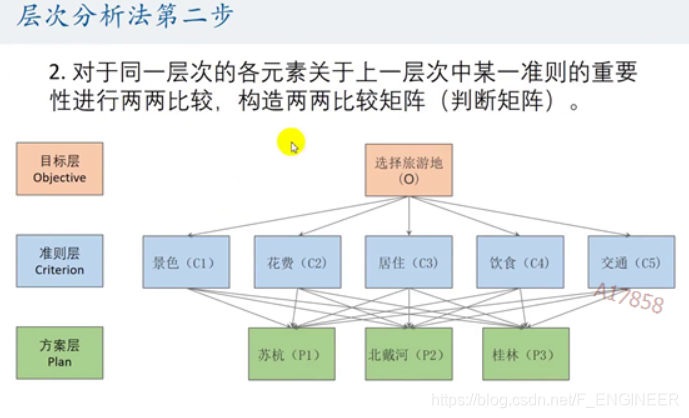
层次分析法判断矩阵:
(1)aij{a}_{ij}aij表示的意义,与指标j相比,i的重要程度
(2)当i=j时,两指标相同,记同等重要1
(3)aij>0{a}_{ij}>0aij>0且满足aij∗aji=1{a}_{ij}*{a}_{ji}=1aij∗aji=1(正互反矩阵)
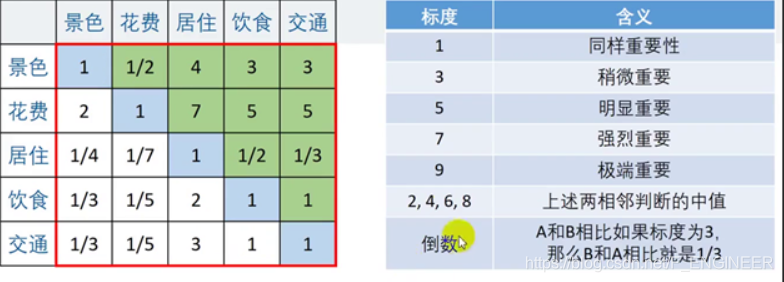
可能出现不一致现象
一致矩阵:各行(各列)成倍数关系aij∗ajk=aik{a}_{ij}*{a}_{jk}={a}_{ik}aij∗ajk=aik
使用判断矩阵求权重前必须进行一致性检验
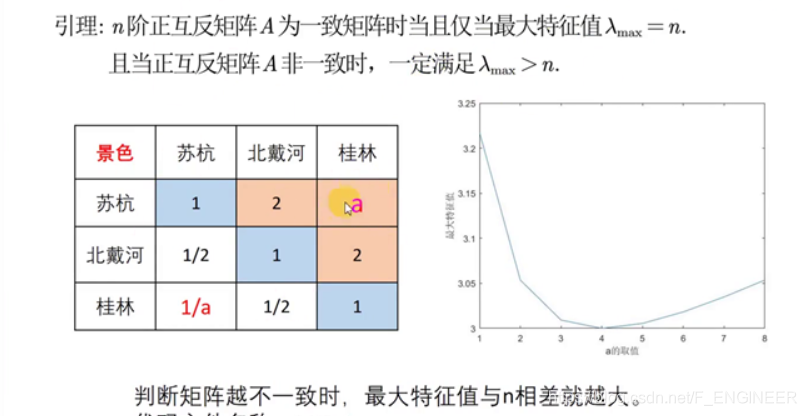
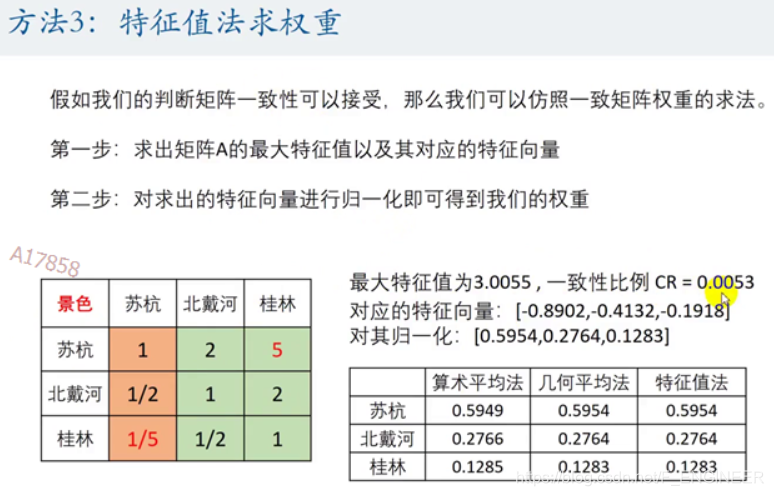
λmaxλmaxλmax为矩阵最大特征值
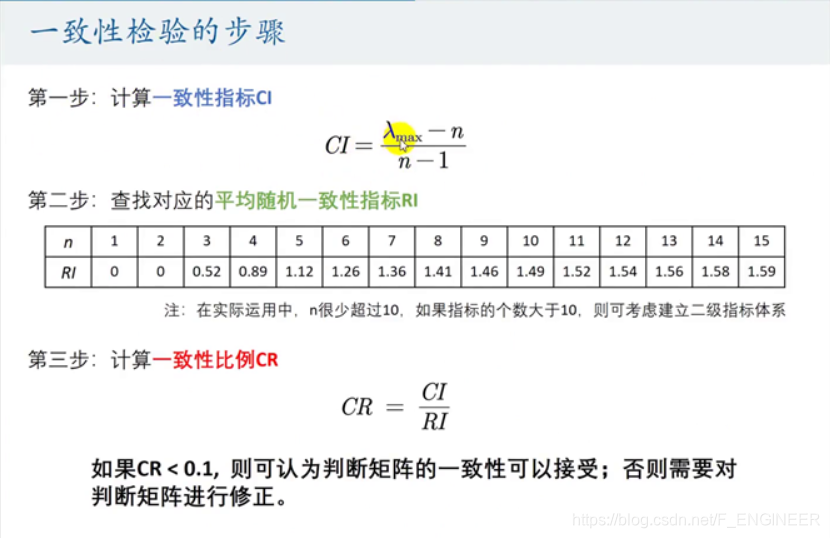

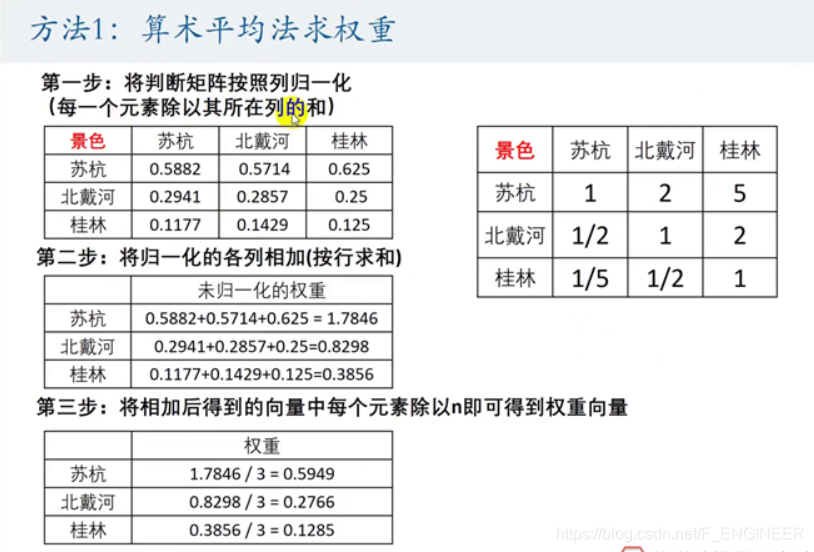


excel计算单元格锁定 F4
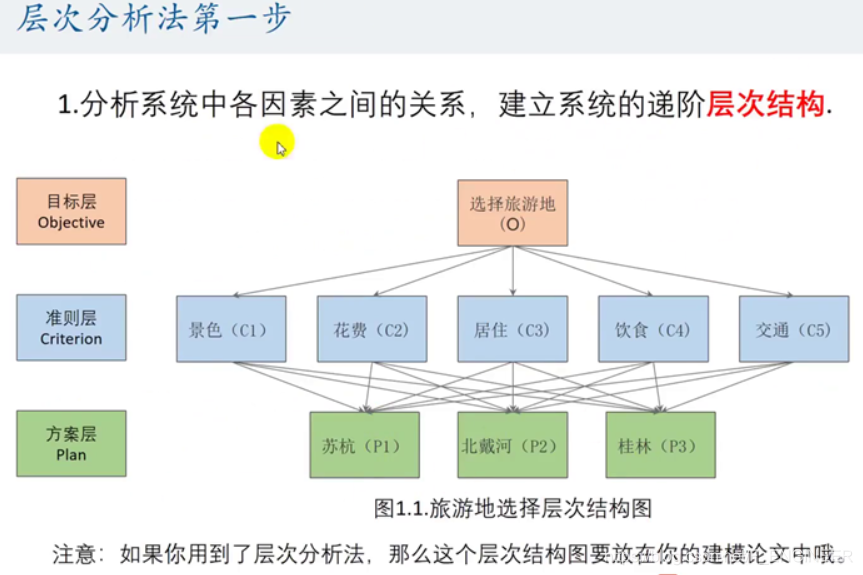
三个层次:目标层(Objective)、准则层(Criterion)、方案层(Plan)
亿图图示:
保存后选择文件——导出&发送——word
将word中图像复制到论文中,加上标题
1.算术平均法 2.几何平均法 3.特征值法
比赛时三种方法都用:(加上如下一段话)
以往的论文利用层次分析法解决实际问题时,都是采用其中某一种方法求全重,而不同计算方法可能导致结果有所偏差。为保证结果的稳健性,本文采用三种方法分别求出权重,再根据得到的权重矩阵计算各方案的得分,并进行排序和综合分析,这样避免了采用单一方法所产生的偏差,得出的结论将更全面、更有效。





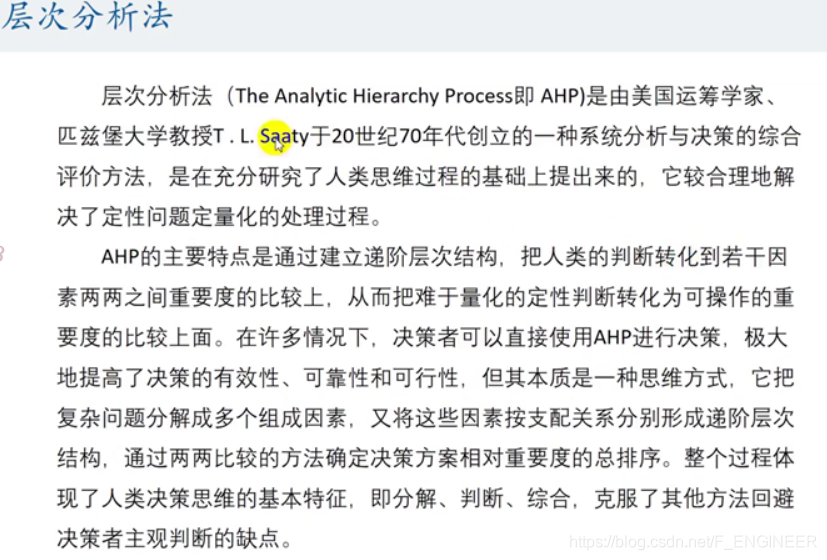
 层次分析法(AHP)是一种解决评价类问题的工具,涉及目标、方案和评价准则三个关键步骤。通过构建判断矩阵进行权重计算,但需先进行一致性检验。文章建议在应用中结合算术平均法、几何平均法和特征值法三种方法求权重,以提高结果的稳健性和准确性。并推荐使用亿图图示软件辅助绘制层次结构图,最终将图像导入论文中进行综合分析。
层次分析法(AHP)是一种解决评价类问题的工具,涉及目标、方案和评价准则三个关键步骤。通过构建判断矩阵进行权重计算,但需先进行一致性检验。文章建议在应用中结合算术平均法、几何平均法和特征值法三种方法求权重,以提高结果的稳健性和准确性。并推荐使用亿图图示软件辅助绘制层次结构图,最终将图像导入论文中进行综合分析。

















 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








