对矢量和矩阵的一些熟悉对于理解量子计算至关重要。 我们在下面简要介绍一下,感兴趣的读者推荐阅读线性代数的标准参考文献,如Strang,G。(1993)。 线性代数导论(第3卷)。 威尔斯利,马萨诸塞州:韦尔斯利 - 剑桥出版社或线性代数等在线参考文献。
维度(或大小)n
的列向量(或简单的向量)v是排列为列的n复数(v1,v2, ...,vn)的集合:

矢量v的范数定义为  。 如果一个向量的范数是1,则称该向量为单位范数(或者称为单位向量 )。 矢量v的伴随符表示为
。 如果一个向量的范数是1,则称该向量为单位范数(或者称为单位向量 )。 矢量v的伴随符表示为 ,并被定义为以下行向量,其中∗表示复共轭,
,并被定义为以下行向量,其中∗表示复共轭,

将两个向量相乘的最常见方法是通过内部产品 ,也称为点积。 内积给出了一个向量到另一个向量的投影,并且在描述如何将一个向量表示为其他更简单向量的和时是非常有用的。 u和v之间的内积,表示为  被定义为
被定义为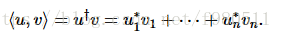 这个表示法还允许将矢量v的标准写为
这个表示法还允许将矢量v的标准写为
我们可以用一个数字c乘以一个向量形成一个新的向量,其条目乘以c。 我们还可以添加两个向量u和v以形成一个新的向量,其条目是u和v条目的总和。 这些操作如下所示:

大小为m * n的矩阵是以m行和n列排列的mn复数的集合,如下所示:

注意维数n的矢量只是一个大小为n * 1的矩阵。 和向量一样,我们可以乘以一个数c的矩阵,得到一个新的矩阵,其中每一项与c相乘,我们可以添加两个相同大小的矩阵来产生一个新的矩阵,其条目是和两个矩阵各自的条目。
矩阵乘法和张量产品
我们还可以乘以两个矩阵M的维数m * n和N的维数n * p得到一个新矩阵P的维数m * p,如下所示:

其中P的条目是 。 例如,条目P11是第一行M与第一列N
。 例如,条目P11是第一行M与第一列N
的内积。 请注意,由于矢量只是矩阵的一种特殊情况,因此此定义扩展到矩阵矢量乘法。
我们考虑的所有矩阵要么是行矩阵,其中行和列的数量是相等的,或者是向量,这只对应于1
列。 一个特殊的方形矩阵是单位矩阵,表示为 1,它的所有对角元素等于1,其余元素等于0:
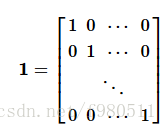
对于方阵A,如果AB=BA= 1,我们说矩阵B是它的逆矩阵。 矩阵的逆矩阵不需要存在,但是当它存在时它是唯一的,我们表示它A−1。对于任何矩阵M,M的伴随或共轭转置是一个矩阵N,使得 。 M伴随物通常表示为
。 M伴随物通常表示为 。 我们说如果
。 我们说如果 或者等价地U−1=
或者等价地U−1= ,则矩阵U是单一的。 也许酉矩阵最重要的属性是它们保持向量的规范。 这是因为
,则矩阵U是单一的。 也许酉矩阵最重要的属性是它们保持向量的规范。 这是因为

如果 ,则矩阵M被认为是Hermitian。
,则矩阵M被认为是Hermitian。
最后,两个矩阵M大小m *n和N大小p * q的张量积(或Kronecker乘积)是一个更大的矩阵P=M N size mp *nq,并从M和N获得,如下所示:
N size mp *nq,并从M和N获得,如下所示:

举一些例子来更好地说明这一点:
 和
和

围绕张量产品的最后一个有用的符号约定是,对任何向量v或矩阵M, 是一个n折叠重复张量积。 例如:
是一个n折叠重复张量积。 例如:
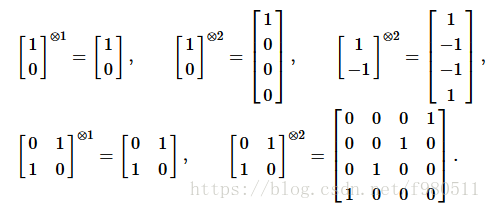

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








