机器学习(Machine Learning,ML)就是让计算机从数据中进行自动学习,得到某种知识(或规律)。
以下内容均为 https//nndl.github.io/nndl-book.pdf的学习笔记。
一.基本概念
1.名词
特征(feature) 标签(label)
样本(sample)/示例(instance):标记好样特征以及对应标签的数据。
数据集(Data set):一组样本构成的集合。数据集分为训练集(Training set) 与测试集(Test set),训练集用于训练模型,测试集用于检验模型好坏。
特征向量(Feature Vector):用一个𝐷 维向量𝒙 = [𝑥1, 𝑥2, ⋯ , 𝑥𝐷]T 表示一个样本的所有特征构成的向量。每一维表示一个特征。标签用y表示。
2.训练/学习过程
假设训练集𝒟 由𝑁 个样本组成,其中每个样本都是独立同分布的(Identically and Independently Distributed,IID),即独立地从相同的数据分布中抽取的,记为:
𝒟 = {(𝒙(1), 𝑦(1)), (𝒙(2), 𝑦(2)), ⋯ , (𝒙(𝑁), 𝑦(𝑁))}. (2.1)
*(注意:独立同分布的即每个样本(𝒙, 𝑦) ∈ 𝒳 × 𝒴 是从𝒳 和𝒴 的联合空间中按照某个未知分布𝑝𝑟(𝒙, 𝑦) 独立地随机产生的.这里要求样本分布𝑝𝑟(𝒙, 𝑦) 必须是固定的(虽然可以是未知的),不会随时间而变化)*
给定训练集𝒟,我们希望让计算机从一个函数集合ℱ = {𝑓1(𝒙), 𝑓2(𝒙), ⋯} 中自动寻找一个“最优”的函数𝑓∗(𝒙) 来近似每个样本的特征向量𝒙 和标签𝑦 之间的真实映射关系.对于一个样本𝒙,我们可以通过函数𝑓∗(𝒙) 来预测其标签的值:
𝑦̂ = 𝑓∗(𝒙), (2.2)
或标签的条件概率:
𝑝(̂ 𝑦|𝒙) = 𝑓∗𝑦 (𝒙). (2.3)
如何寻找这个“最优”的函数𝑓∗(𝒙) 是机器学习的关键,一般需要通过学习算法(Learning Algorithm)𝒜 来完成.
在有些文献中, 学习算法也叫作学习器(Learner).这个寻找过程通常称为**学习(Learning)或训练(Training)**过程.
3.测试过程
使用学习到的函数𝑓∗(𝒙) 来预测芒测试样本的好坏.为了评价的公正性,我们还是独立同分布地抽取一组样本作为测试集𝒟′,并在测试集进行测试,计算预测结果的准确率:
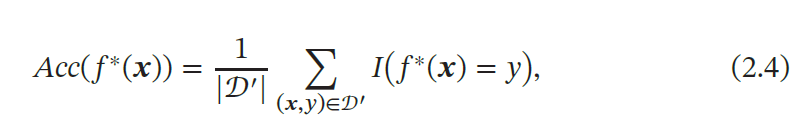
其中𝐼(⋅) 为指示函数,|𝒟′| 为测试集大小.
4.总结
综上所述,机器学习系统如下所示:
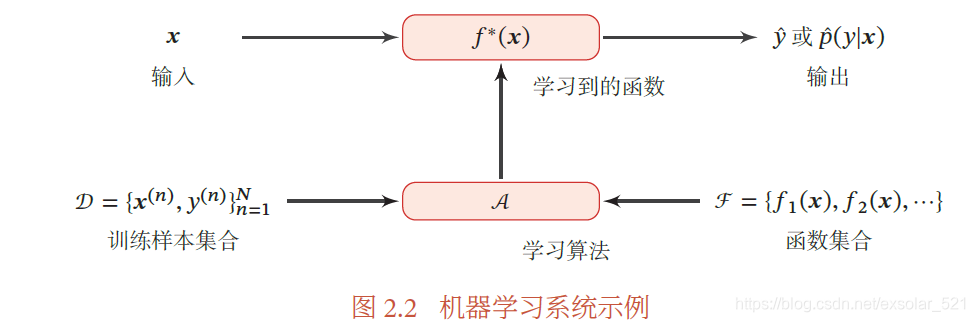
二.机器学习的三个基本要素
1.模型
输入空间𝒳 和输出空间𝒴 构成了一个样本空间.对于样本空间中的样本**(𝒙, 𝑦) ∈ 𝒳 × 𝒴**,假定𝒙 和𝑦 之间的关系可以通过一个未知的真实映射函数𝑦 =𝑔(𝒙) 或真实条件概率分布𝑝𝑟(𝑦|𝒙)来描述.机器学习的目标是找到一个模型来近似 真实映射函数𝑔 ∶ 𝒳 → 𝒴.似真实映射函数𝑔(𝒙) 或真实条件概率分布𝑝𝑟(𝑦|𝒙).
由于我们不知道真实的映射函数𝑔(𝒙) 或条件概率分布𝑝𝑟(𝑦|𝒙) 的具体形式,因而只能根据经验来假设一个函数集合ℱ,称为假设空间(Hypothesis Space),然后通过观测其在训练集𝒟 上的特性,从中选择一个理想的假设(Hypothesis)𝑓∗ ∈ ℱ.
假设空间ℱ 通常为一个参数化的函数族
ℱ = {𝑓(𝒙; 𝜃)|𝜃 ∈ ℝ𝐷}, (2.5)
其中𝑓(𝒙; 𝜃) 是参数为𝜃 的函数,也称为模型(Model),𝐷 为参数的数量.
常见的假设空间可以分为线性和非线性两种,对应的模型𝑓 也分别称为线性模型和非线性模型.
1)线性模型
线性模型的假设空间为一个参数化的线性函数族,即对于分类问题,一般为广义线性函数,参见公式:
𝑓(𝒙; 𝜃) = 𝒘T𝒙 + 𝑏, (2.6)
其中参数𝜃 包含了权重向量𝒘 和偏置𝑏.
2)非线性模型
广义的非线性模型可以写为多个非线性基函数𝜙(𝒙) 的线性组合
𝑓(𝒙; 𝜃) = 𝒘T𝜙(𝒙) + 𝑏, (2.7)
其中𝜙(𝒙) = [𝜙1(𝒙), 𝜙2(𝒙), ⋯ , 𝜙𝐾 (𝒙)]T 为𝐾 个非线性基函数组成的向量,参数𝜃包含了权重向量𝒘 和偏置𝑏.
如果𝜙(𝒙) 本身为可学习的基函数,比如
𝜙𝑘(𝒙) = ℎ(𝒘T𝑘𝜙′(𝒙) + 𝑏𝑘), ∀1 ≤ 𝑘 ≤ 𝐾, (2.8)
其中ℎ(⋅) 为非线性函数,𝜙′(𝒙) 为另一组基函数,𝒘𝑘 和𝑏𝑘 为可学习的参数,则𝑓(𝒙; 𝜃) 就等价于神经网络模型.
2.学习准则
1)一个好的模型所需条件
一个好的模型𝑓(𝒙, 𝜃∗) 应该在所有(𝒙, 𝑦) 的可能取值上都与真实映射函数𝑦 = 𝑔(𝒙) 一致,即
|𝑓(𝒙, 𝜃∗) − 𝑦| < 𝜖, ∀(𝒙, 𝑦) ∈ 𝒳 × 𝒴, (2.9)
或与真实条件概率分布𝑝𝑟(𝑦|𝒙) 一致,即
|𝑓𝑦(𝒙, 𝜃∗) − 𝑝𝑟(𝑦|𝒙)| < 𝜖, ∀(𝒙, 𝑦) ∈ 𝒳 × 𝒴, (2.10)
其中**𝜖** 是一个很小的正数,**𝑓𝑦(𝒙, 𝜃∗)** 为模型预测的条件概率分布中𝑦 对应的概率.
2)模型好坏评价-期望风险
模型𝑓(𝒙; 𝜃) 的好坏可以通过期望风险(Expected Risk/Error)ℛ(𝜃) 来衡量,其定义为
ℛ(𝜃) = 𝔼(𝒙,𝑦)∼𝑝𝑟(𝒙,𝑦)[ℒ(𝑦, 𝑓(𝒙; 𝜃))], (2.11)
其中𝑝𝑟(𝒙, 𝑦) 为真实的数据分布,ℒ(𝑦, 𝑓(𝒙; 𝜃)) 为损失函数,用来量化两个变量之间的差异.
2.1损失函数
损失函数:非负实数函数,用来量化实际值与预测值之间的差异。
| 函数形式 | 优缺点 |
|---|---|
0-1损失函数((0-1 Loss Function)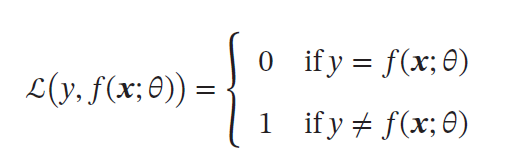 | 不连续且导数为0,难以优化 |
平方损失函数(Quadratic Loss Function) | 一般不适用于分类问题 |
交叉熵损失函数(Cross-Entropy Loss Function)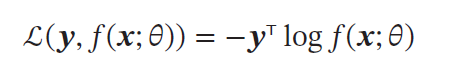 | 当y为one-hot编码时,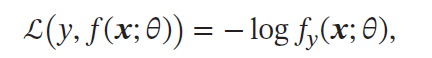 为负对数似然函数,用于分类 为负对数似然函数,用于分类 |
Hinge 损失函数(Hinge Loss Function)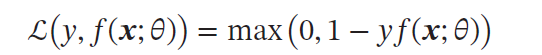 | 主要用于支持向量机(SVM) 中 |
2.2风险最小化准则
真实数据分布和映射关系实际未知,无法计算期望风险,但可在训练集上计算经验风险Empirical Risk)**,,即在训练集上的平均损失:
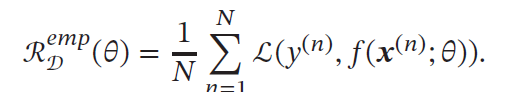
经验风险最小化(Empirical Risk Minimization,ERM)准则:是找到一组参数𝜃∗ 使得经验风险最小。
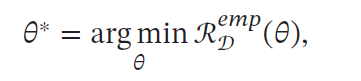





 本文深入解析了机器学习的基本概念,包括特征、标签、样本、数据集等关键术语,并详细介绍了机器学习的训练与测试过程。此外,还探讨了模型、学习准则及损失函数等核心要素。
本文深入解析了机器学习的基本概念,包括特征、标签、样本、数据集等关键术语,并详细介绍了机器学习的训练与测试过程。此外,还探讨了模型、学习准则及损失函数等核心要素。
















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








