IDA*学习笔记-HDU1667 The Rotation Game-优快云博客

本文链接：https://blog.youkuaiyun.com/ex_voda/article/details/126041946

本文详细介绍了如何运用IDA*算法解决旋转游戏的优化问题，通过对比IDDFS，阐述了A*算法如何提升搜索效率，重点讨论了估价函数的设计思路，并给出了完整的C++实现代码。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

本文将以HDU1667为例，记录笔者学习IDA*的心路历程与一些浅见。本文将着重与上一篇IDDFS的笔记进行联系，比较IDA*与IDDFS的特征区别，同时修正一些对于迭代加深算法的见解。

首先上题：

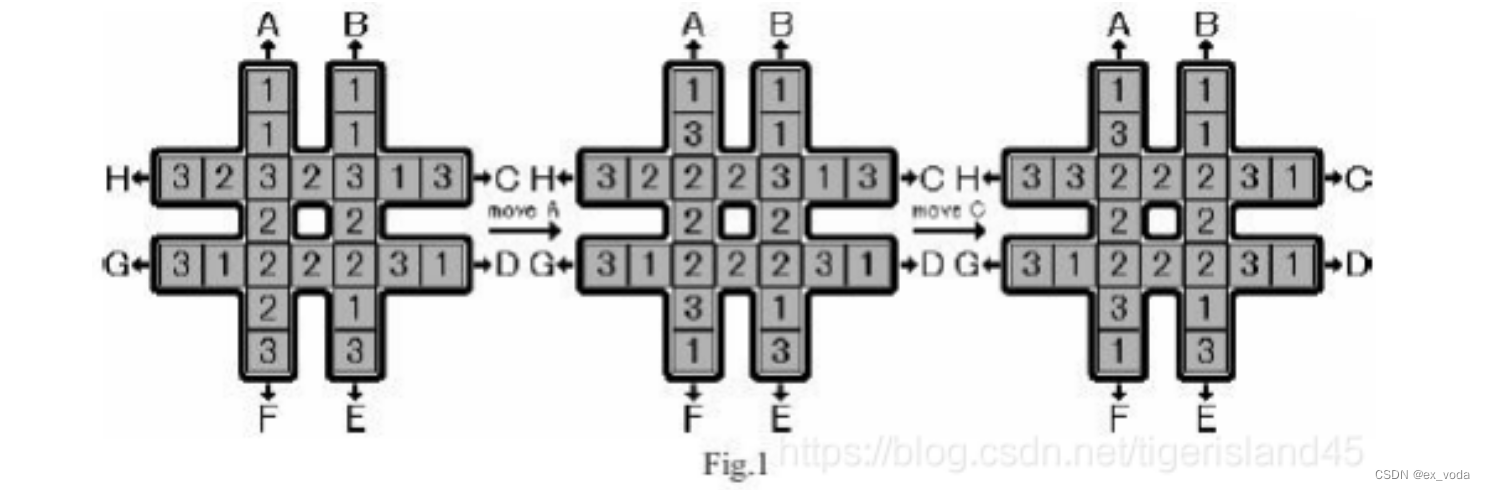
旋转游戏使用一个#形状的板，可以容纳24块方块(见图1)。方块上标着符号1、2和3，每种方块都有8块。
最初，方块是随机放置在棋盘上的。你的任务是移动方块，使放置在中心广场的八个方块有相同的标记。这里只有一种有效的移动类型，即旋转4行中的1行，每一行由7个块组成。即将一行中的6个block向头部移动1个block，将头部block移动到行尾。8种可能的走法用大写字母A到H标出。图1展示了两个连续的走法，从某个初始配置移动A和移动C。

Input:
输入不超过30个测试用例。每个测试用例只有一行包含24个数字，这是初始配置中的块的符号。块的行是从上到下列出的。对于每一行，代码块从左到右列出。这些数字用空格隔开。例如，样本输入中的第一个测试用例对应于图1中的初始配置。案例之间没有空白行。在结束输入的最后一个测试用例之后，有一行包含一个' 0 '。
Output:
对于每个测试用例，您必须输出两行。第一行包含到达最终配置所需的所有步骤。每一步都是一个字母，从A到H ，行内字母之间不能有空格。如果不需要移动，则输出“no moves needed”。在第二行中，您必须在这些移动之后输出中心方块中的方块符号。如果有几种可能的解决方案，你必须输出使用最少移动次数的那一种。如果仍然有多个可能的解决方案，您必须输出的解决方案中最小的字典顺序的字母的移动。case之间不需要输出空行。

Sample Input
1 1 1 1 3 2 3 2 3 1 3 2 2 3 1 2 2 2 3 1 2 1 3 3
1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 3 3 3 3 3 3 3 3
0
Sample Output
AC
2
DDHH
2

对于IDA*而言，相较于IDDFS最大的地方是A*，即贪心算法的加入，具体来说就是增加了估价函数，作用与IDDFS中的迭代加深部分，用于限制IDDFS对DFS深度的规定数量，在很多题目中体现为不进行过小的深度计算，例如在HDU1560 DNA sequence中，小于输入中最小的DNA链的长度的枚举深度都是无效的等等。由于IDDFS的大量枚举时间都不由得地浪费在反复迭代加深的过程中，高效的估价函数能大大避免时间的浪费。

在上一篇IDDFS-埃及分数的笔记中，由于埃及分数题目的特殊性，我们无法加入合适的A*算法，而是只能在其中BFS部分加入划界函数规定它的有效宽度，使得题目至少在一个方向上是有限的，这至少给我们了一点原则性的启发：“避免无限、避免浪费。”便是IDDFS和IDA*的优化方向。

而在这道题中，解题的基本思路比较明确，题目已经给出了明确的值位移方式（旋转），无非就是用各位各自喜好的数据结构去储存和操作。笔者选择了字符串。

讲讲笔者自己的估价函数构造思路：在本题中，我们更关注的是中间8个方块的数值（有效区域）是否一样，而鉴于“旋转”这种操作，每旋转一次会有一个数字进入有效区域，一个数字离开有效区域，“一进一出”意味着一次旋转最多改变有效区域内两个方块的值，因此如果方块内不一样数字的个数除2＞剩下的旋转次数（总深度减当前深度），则说明深度不够，不再枚举，跳过。

先放出估价函数的代码：

bool check(int delta){		//IDA*-剪枝 
	int sum = 0;
	string str;
	str = a[2]+c[3]+b[2]+b[3]+b[4]+d[3]+a[4]+a[3];
	for(int i=0;i<str.length()-1;i++){
		if(str[i]==str[i+1])	sum++;
	}
	return(sum/2>delta);
}

实际上估价函数（剪枝）的部分往往可以是最后思考的内容。解决了A*问题，让我们重新回到题目本身，首先明确IDDFS中DFS深度的数据意义，本题显然是旋转次数（往往深度和所求最优解统一数据意义），明确了这点，DFS部分基本完成了80%，接下来思考一下BFS广度搜索部分。

在DFS的内部，IDDFS往往需要一个BFS来完成搜索任务，本题与埃及分数不同，值位移的方向是有限的（8个旋转方向），即宽度是有限的，因此不需要划界函数来限制它（有的题目仍需要在BFS部分进一步优化）。有趣的是，宽度有限的BFS组成的IDFFS往往不需要队列的加入，因为它的数值变化方向是一定的，所以事实上DFS的回溯完成了队列queue的工作，并且比queue更好！

首先给出值位移函数模块，由于用字符串储存数据，所以值位移函数是一个大switch，但操作并不复杂，同时按字典序排列，直接解决了题目要求的字典序问题：

void align(char i){	//动了谁，就以谁为标注对齐4个字符串 
	switch(i){
		case 'A':
		case 'B':
		case 'E':
		case 'F':{
			c[2] = a[2];	c[4] = b[2];
			d[2] = a[4];	d[4] = b[4];
			break;
		}
		case 'C':
		case 'D':
		case 'G':
		case 'H':
			a[2] = c[2];	b[2] = c[4];
			a[4] = d[2];	b[4] = d[4];
			break;
	}
}
string move(char i){	//1=A,2=B,3=C,4=D,5=G,6=H,7=E,8=F	9-X=X的对面 
	string str;
	switch(i){
		case 'A':{
			char ch = a[0];
			for(int i=0;i<6;i++){
				a[i] = a[i+1];
			}
			a[6] = ch;
			str = "A";
			break;
		}
		case 'B':{
			char ch = b[0];
			for(int i=0;i<6;i++){
				b[i] = b[i+1];
			}
			b[6] = ch;
			str = "B";
			break;
		}
		case 'C':{
			char ch = c[6];
			for(int i=6;i>0;i--){
				c[i] = c[i-1];
			}
			c[0] = ch;
			str = "C";
			break;
		}
		case 'D':{
			char ch = d[6];
			for(int i=6;i>0;i--){
				d[i] = d[i-1];
			}
			d[0] = ch;
			str = "D";
			break;
		}
		case 'G':{
			char ch = d[0];
			for(int i=0;i<6;i++){
				d[i] = d[i+1];
			}
			d[6] = ch;
			str = "G";
			break;
		}
		case 'H':{
			char ch = c[0];
			for(int i=0;i<6;i++){
				c[i] = c[i+1];
			}
			c[6] = ch;
			str = "H";
			break;
		}
		case 'E':{
			char ch = b[6];
			for(int i=6;i>0;i--){
				b[i] = b[i-1];
			}
			b[0] = ch;
			str = "E";
			break;
		}
		case 'F':{
			char ch = a[6];
			for(int i=6;i>0;i--){
				a[i] = a[i-1];
			}
			a[0] = ch;
			str = "F";
			break;
		}
	}
	align(i);
	return str;
}

对当前值进行位移，然后检测它，放出结果判断函数，一个简单粗暴的枚举判断：

bool finish(){
	return(a[2]==c[3] && c[3]==b[2] && b[2]==b[3] && b[3]==b[4] && b[4]==d[3] && d[3]==a[4] && a[4]==a[3] && a[3]==a[2]);
}

有了上面这些模块，IDA*部分的代码将变得简单，不过记得储存路径，本题用map<string,string>记录位移，回溯则删除末位：

bool IDA(int now, int deep){
	if(finish()){
		if(deep==0)	cout<<"no moves needed"<<endl;
		else	cout<<load<<endl;
		cout<<a[2]<<endl;
		return true;
	}
	if(check(deep-now))	return false;
	if(now == deep)		return false;
	for(char i='A';i<='H';i++){		//IDA-BFSg
		string st;
		st = move(i);
		load += st;
		if(IDA(now+1,deep))	return true;
		move(m[i]);
		load.pop_back();
	}
	return false;
}

最后附赠打印代码，整合，给出源码：

#include<bits/stdc++.h>
using namespace std;

string a, b, c, d; 
string load;
map<char,char> m;
void align(char i){	//动了谁，就以谁为标注对齐4个字符串 
	switch(i){
		case 'A':
		case 'B':
		case 'E':
		case 'F':{
			c[2] = a[2];	c[4] = b[2];
			d[2] = a[4];	d[4] = b[4];
			break;
		}
		case 'C':
		case 'D':
		case 'G':
		case 'H':
			a[2] = c[2];	b[2] = c[4];
			a[4] = d[2];	b[4] = d[4];
			break;
	}
}
string move(char i){	//1=A,2=B,3=C,4=D,5=G,6=H,7=E,8=F	9-X=X的对面 
	string str;
	switch(i){
		case 'A':{
			char ch = a[0];
			for(int i=0;i<6;i++){
				a[i] = a[i+1];
			}
			a[6] = ch;
			str = "A";
			break;
		}
		case 'B':{
			char ch = b[0];
			for(int i=0;i<6;i++){
				b[i] = b[i+1];
			}
			b[6] = ch;
			str = "B";
			break;
		}
		case 'C':{
			char ch = c[6];
			for(int i=6;i>0;i--){
				c[i] = c[i-1];
			}
			c[0] = ch;
			str = "C";
			break;
		}
		case 'D':{
			char ch = d[6];
			for(int i=6;i>0;i--){
				d[i] = d[i-1];
			}
			d[0] = ch;
			str = "D";
			break;
		}
		case 'G':{
			char ch = d[0];
			for(int i=0;i<6;i++){
				d[i] = d[i+1];
			}
			d[6] = ch;
			str = "G";
			break;
		}
		case 'H':{
			char ch = c[0];
			for(int i=0;i<6;i++){
				c[i] = c[i+1];
			}
			c[6] = ch;
			str = "H";
			break;
		}
		case 'E':{
			char ch = b[6];
			for(int i=6;i>0;i--){
				b[i] = b[i-1];
			}
			b[0] = ch;
			str = "E";
			break;
		}
		case 'F':{
			char ch = a[6];
			for(int i=6;i>0;i--){
				a[i] = a[i-1];
			}
			a[0] = ch;
			str = "F";
			break;
		}
	}
	align(i);
	return str;
}
bool check(int delta){		//IDA*-剪枝 
	int sum = 0;
	string str;
	str = a[2]+c[3]+b[2]+b[3]+b[4]+d[3]+a[4]+a[3];
	for(int i=0;i<str.length()-1;i++){
		if(str[i]==str[i+1])	sum++;
	}
	return(sum/2>delta);
}
bool finish(){
	return(a[2]==c[3] && c[3]==b[2] && b[2]==b[3] && b[3]==b[4] && b[4]==d[3] && d[3]==a[4] && a[4]==a[3] && a[3]==a[2]);
}
void print(){		//debug用打印函数，release中不需要 
	cout<<"   A B"<<endl
		<<"   "<<a[0]<<" "<<b[0]<<endl
		<<"   "<<a[1]<<" "<<b[1]<<endl
		<<"H"<<c[0]<<c[1]<<c[2]<<c[3]<<c[4]<<c[5]<<c[6]<<"C"<<endl
		<<"   "<<a[3]<<" "<<b[3]<<endl
		<<"G"<<d[0]<<d[1]<<d[2]<<d[3]<<d[4]<<d[5]<<d[6]<<"D"<<endl
		<<"   "<<a[5]<<" "<<b[5]<<endl
		<<"   "<<a[6]<<" "<<b[6]<<endl
		<<"   F E"<<endl;
		cout<<endl;
}
bool IDA(int now, int deep){
	if(finish()){
		if(deep==0)	cout<<"no moves needed"<<endl;
		else	cout<<load<<endl;
		cout<<a[2]<<endl;
		return true;
	}
	if(check(deep-now))	return false;
	if(now == deep)		return false;
	for(char i='A';i<='H';i++){		//IDA-BFSg
		string st;
		st = move(i);
		load += st;
		if(IDA(now+1,deep))	return true;
		move(m[i]);
		load.pop_back();
	}
	return false;
}
int main(){
	m['A'] = 'F'; m['B'] = 'E'; m['C'] = 'H'; m['D'] = 'G';
	m['F'] = 'A'; m['E'] = 'B'; m['H'] = 'C'; m['G'] = 'D';
	while(cin>>a[0]){
		if(a[0] == '0')	return 0;
		cin            	>>		b[0]>>
					a[1]>>		b[1]>>
		c[0]>>c[1]>>a[2]>>c[3]>>b[2]>>c[5]>>c[6]>>
					a[3]>>		b[3]>>
		d[0]>>d[1]>>a[4]>>d[3]>>b[4]>>d[5]>>d[6]>>
					a[5]>>		b[5]>>
					a[6]>>		b[6];
		c[2] = a[2];	c[4] = b[2];
		d[2] = a[4];	d[4] = b[4];
		for(int deep=0;;deep++){
			load = "";
			if(IDA(0,deep)) break;
		}
	}
}

最后记录一些要点：

1、IDA*就是在深度上进行优化的IDDFS，基本模块完全一致。

2、选择IDA*的条件：在深度选择上是可以优化的（埃及分数不行，因为答案不可预判）。

3、A*算法的构造：IDDFS均以算出结果为离开深度，因此A*的任务往往是去除过浅的情况。