每日三百行代码 第二十三天
#include <iostream>
#include <queue>
#include <cstring>
#include <stack>
#include <algorithm>
using namespace std;
const int maxn = 505;
int N, M, s, e;
int nums[maxn], dist[maxn];
int tot[maxn], sum[maxn];
int pre[maxn];
bool vis[maxn];
vector<pair<int, int> > E[maxn];
void dijkstra()
{
priority_queue<pair<int, int> > Q;
dist[s] = 0;
Q.push({-dist[s], s});
while (!Q.empty())
{
int head = Q.top().second;
Q.pop();
if (vis[head]) continue;
vis[head] = 1;
for (int i = 0; i < E[head].size(); i ++ )
{
int v = E[head][i].first;
int curdist = E[head][i].second;
if (dist[v] == dist[head] + curdist)
{
tot[v] += tot[head];
sum[v] = max(sum[v], sum[head] + nums[v]);
pre[v] = head;
}
if (dist[v] > dist[head] + curdist)
{
dist[v] = dist[head] + curdist;
tot[v] = tot[head];
sum[v] = sum[head] + nums[v];
pre[v] = head;
Q.push({-dist[v], v});
}
}
}
}
void output(int x)
{
vector<int> path;
for (; x!= -1; x = pre[x])
path.push_back(x);
reverse(path.begin(), path.end());
int n = path.size();
for (int i = 0; i < n; i ++) cout << path[i] << " \n"[i==n-1];
}
int main ()
{
memset(dist, 0x3f, sizeof dist);
memset(pre, -1, sizeof pre);
cin >> N >> M >> s >> e;
for (int i = 0; i < N; i ++ ) cin >> nums[i];
for (int i = 0; i < M; i ++ )
{
int a, b, c;
cin >> a >> b >> c;
E[a].push_back({b, c});
E[b].push_back({a, c});
}
tot[s] = 1;
sum[s] = nums[s];
dijkstra();
cout << tot[e] << " " << sum[e] << endl;
output(e);
return 0;
}
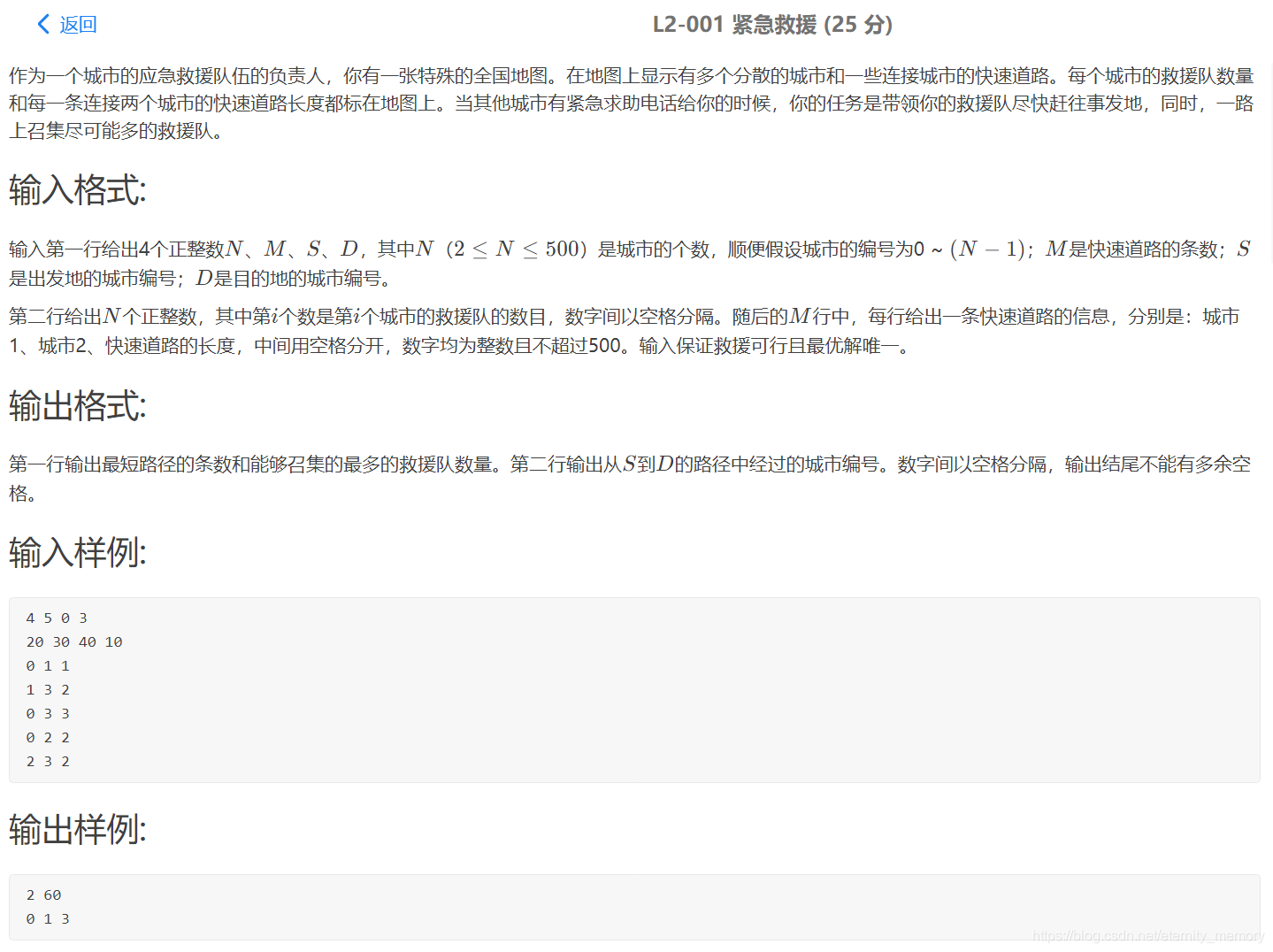
L2-001 紧急救援 (25 分)&&dijkstra
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1000007;
struct Node{
int dt;
int nt;
}a[maxn];
struct Temp{
int ad;
int dt;
int nt;
}a1[maxn],a2[maxn];
int book[maxn];
void print(struct Temp *arr,int n){
if (n==0) return ;
for(int i=0;i<n-1;i++) {
printf("%05d %d %05d\n",arr[i].ad,arr[i].dt,arr[i+1].ad);
}
printf("%05d %d -1\n",arr[n-1].ad,arr[n-1].dt);
}
int main()
{
memset(book,0,sizeof(book));
int fa,n;
scanf("%d%d",&fa,&n);
for(int i=0;i<n;i++) {
int ad,dt,nt;
scanf("%d%d%d",&ad,&dt,&nt);
a[ad].dt = dt;
a[ad].nt = nt;
}
int p = fa;
int cnt2 = 0, cnt1 = 0;
while(p!=-1) {
int t = abs(a[p].dt);
if(book[t]) {
a2[cnt2].ad = p;
a2[cnt2].dt = a[p].dt;
a2[cnt2++].nt = a[p].nt;
} else {
a1[cnt1].ad = p;
a1[cnt1].dt = a[p].dt;
a1[cnt1++].nt = a[p].nt;
}
p = a[p].nt;
book[t]++;
}
print(a1,cnt1);
print(a2,cnt2);
return 0;
}
#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
const int maxn = 1e5;
struct Node{
int address;
int key;
int next;
int num;
}node[maxn];
bool vis[maxn];
bool cmp(Node a,Node b){
return a.num<b.num;
}
int main()
{
int head,n,a;
scanf("%d%d",&head,&n);
int k1=0,k2=0;
for(int i=0;i<maxn;i++){
node[i].num=2*maxn;
}
for(int i=0;i<n;i++){
scanf("%d",&a);
scanf("%d%d",&node[a].key,&node[a].next);
node[a].address=a;
}
for(int i=head;i!=-1;i=node[i].next){
if(!vis[abs(node[i].key)]){
vis[abs(node[i].key)]=true;
node[i].num=k1;
k1++;
}else{
node[i].num=maxn+k2;
k2++;
}
}
sort(node,node+maxn,cmp);
int k=k1+k2;
for(int i=0;i<k;i++){
if(i!=k1-1&&i!=k-1){
printf("%05d %d %05d\n",node[i].address,node[i].key,node[i+1].address);
}else{
printf("%05d %d -1\n",node[i].address,node[i].key);
}
}
return 0;
}
#include<bits/stdc++.h>
using namespace std;
struct E
{
float amount;
float price;
float avg;
}buf[1111];
bool cmp(E a,E b)
{
return a.avg>b.avg;
}
int main()
{
int n,m,t,i;
float sum;
sum=t=0;
scanf("%d%d",&n,&m);
for(i=0;i<n;i++)
{
scanf("%f",&buf[i].amount);
}
for(i=0;i<n;i++)
{
scanf("%f",&buf[i].price);
}
for(i=0;i<n;i++)
{
buf[i].avg=buf[i].price/buf[i].amount;
}
sort(buf,buf+n,cmp);
for(i=0;i<n;i++)
{if(buf[i].amount<=m){
sum+=buf[i].price;}
else
{
sum+=buf[i].avg*m;
break;
}
m=m-buf[i].amount;
}
printf("%.2f",sum);
return 0;
}
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
const int maxn = 10000;
#define mem(a) memset(a,0,sizeof(a))
#define inf 0x3f3f3f3f
typedef struct {
double have_sum,sale_sum,rate;
}node;
node a[maxn];
bool cmp(node a,node b)
{
return a.rate > b.rate;
}
int main()
{
int n;
double need;
cin>>n>>need;
for(int i = 0;i < n;i++)
cin>>a[i].have_sum;
for(int i = 0;i < n;i++)
{
cin>>a[i].sale_sum;
a[i].rate =a[i].sale_sum/(a[i].have_sum*1.0);
}
sort(a,a+n,cmp);
int cnt = 0;
double sum = 0;
while(need > 0 && cnt < n)
{
if(need < a[cnt].have_sum)
{
sum += need * a[cnt].rate;
need = 0;
}
else
{
sum += a[cnt].sale_sum;
need -= a[cnt].have_sum;
}
cnt++;
}
printf("%.2lf\n",sum);
return 0;
}
在这里插入代码片
#include<cstdio>
using namespace std;
const int maxn=1000+10;
int a[maxn];
int count=0;
bool istrue(int left,int right)
{
int k=left+1;
int count=0;
if(left>=right)
return true;
for(int i=left+1;i<=right;i++)
{
if(a[i]>=a[left]&&count==0)
{
k=i;
count++;
}
else if(count!=0&&a[i]<a[left])
return false;
}
if(istrue(left+1,k-1)&&istrue(k,right))
return true;
else
return false;
}
void post(int left,int right)
{
int k=left+1;
if(left>right)
return ;
else if(left==right)
{
if(count==0)
{
printf("%d",a[left]);
count++;
}
else
printf(" %d",a[left]);
return;
}
for(int i=left+1;i<=right;i++)
{
if(a[i]>=a[left])
{
k=i;
break;
}
}
post(left+1,k-1);
post(k,right);
printf(" %d",a[left]);
return;
}
bool istrue1(int left,int right)
{
int k=left+1;
int count=0;
if(left>=right)
return true;
for(int i=left+1;i<=right;i++)
{
if(a[i]<a[left]&&count==0)
{
k=i;
count++;
}
else if(count!=0&&a[i]>=a[left])
return false;
}
if(istrue1(left+1,k-1)&&istrue1(k,right))
return true;
else
return false;
}
void post1(int left,int right)
{
int k=left+1;
if(left>right)
{
return ;
}
else if(left==right)
{
if(count==0)
{
printf("%d",a[left]);
count++;
}
else
printf(" %d",a[left]);
return;
}
for(int i=left+1;i<=right;i++)
{
if(a[i]<a[left])
{
k=i;
break;
}
}
post1(left+1,k-1);
post1(k,right);
printf(" %d",a[left]);
return;
}
int main()
{
int n;
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
}
bool isless=true;
if(a[1]>a[2])
{
bool ans=istrue(1,n);
if(ans==true)
{
printf("YES\n");
post(1,n);
}
else
printf("NO\n");
}
else
{
bool ans=istrue1(1,n);
if(ans==true)
{
printf("YES\n");
post1(1,n);
}
else
printf("NO\n");
}
}
#include<iostream>
#include<stdio.h>
#include<set>
#include<algorithm>
#include<cmath>
#include<map>
#include<vector>
#include<string.h>
#include<stack>
#include<cctype>
#include<map>
#include<queue>
#include<sstream>
using namespace std;
#define inf 0x3f3f3f3f
typedef long long ll;
typedef struct node* Tree;
struct node{
int data;
Tree l,r;
};
int pre[1001],n,flagBST=1,flagMirroBST=1,flag=0;
Tree buildBST(int pre[],int n)
{
if(!n) return NULL;
Tree temp=new struct node;
temp->data=pre[0];
int i,j;
for(i=1;i<n;i++)
{
if(pre[i]>=temp->data) break;
}
for(j=i;j<n;j++)
{
if(pre[j]<temp->data)
{
flagBST=0;
return NULL;
}
}
temp->l=buildBST(pre+1,i-1);
temp->r=buildBST(pre+i,n-i);
return temp;
}
Tree buildMirroBST(int pre[],int n)
{
if(!n) return NULL;
Tree temp=new struct node;
temp->data=pre[0];
int i,j;
for(i=1;i<n;i++)
{
if(pre[i]<temp->data) break;
}
for(j=i;j<n;j++)
{
if(pre[j]>=temp->data)
{
flagMirroBST=0;
return NULL;
}
}
temp->l=buildMirroBST(pre+1,i-1);
temp->r=buildMirroBST(pre+i,n-i);
return temp;
}
void Print(Tree t)
{
if(t)
{
Print(t->l);
Print(t->r);
if(!flag) {printf("%d",t->data);flag=1;}
else printf(" %d",t->data);
}
}
int main()
{
cin>>n;
for(int i=0;i<n;i++) cin>>pre[i];
Tree t,tm;
t=buildBST(pre,n);
tm=buildMirroBST(pre,n);
if(t && flagBST)
{
printf("YES\n");
Print(t);
printf("\n");
}
else if(tm && flagMirroBST)
{
printf("YES\n");
Print(tm);
printf("\n");
}
else printf("NO\n");
return 0;
}
#include<bits/stdc++.h>
using namespace std;
set<int> s[55];
int main()
{
int n;
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
int m,x;
scanf("%d",&m);
while(m--)
{
scanf("%d",&x);
s[i].insert(x);
}
}
int k,a,b;
scanf("%d",&k);
while(k--)
{
scanf("%d%d",&a,&b);
int ans1=s[a].size();
int ans2=s[b].size();
int ans3=0;
for(set<int>::iterator it=s[a].begin();it!=s[a].end();++it)
{
if(s[b].find(*it)!=s[b].end())
{
ans3++;
}
}
printf("%.2lf%%\n",ans3*1.0/(ans1+ans2-ans3)*100);
}
return 0;
}
#include<cstdio>
#include<set>
using namespace std;
set<int> s[55];
int main()
{
int n;
scanf("%d",&n);
for(int i=1;i<=n;i++){
int m,x;
scanf("%d",&m);
while(m--){
scanf("%d",&x);
s[i].insert(x);
}
}
int k,a,b;
scanf("%d",&k);
while(k--){
scanf("%d%d",&a,&b);
int cnta=s[a].size(),cntb=s[b].size(),cnt=0;
for(set<int>::iterator it=s[a].begin();it!=s[a].end();++it){
if(s[b].find(*it)!=s[b].end()){
cnt++;
}
}
printf("%.2lf%\n",cnt*1.0/(cnta+cntb-cnt)*100);
}
return 0;
}
#include<iostream>
#include<vector>
#include<cstdio>
#include<queue>
#include<set>
using namespace std;
int n;
set<int> u[55];
void find(int a,int b){
int same=0;
set<int>::iterator it;
for(it=u[a].begin();it!=u[a].end();it++){
if(u[b].find(*it)!=u[b].end()) same++;
}
int sum=u[a].size()+u[b].size();
int nt=sum-same;
printf("%.2lf\%\n",same*1.0/nt*100);
}
int main(){
cin>>n;
int k;
int a;
int m;
for(int i=1;i<=n;i++){
cin>>k;
for(int j=0;j<k;j++){
scanf("%d",&a);
u[i].insert(a);
}
}
cin>>m;
int b;
for(int i=0;i<m;i++){
scanf("%d%d",&a,&b);
find(a,b);
}
}
本文介绍了Dijkstra算法在紧急救援路径规划中的应用，通过优化求解起点到终点的最短路径，并考虑了路径上的救援人数最大化。同时展示了多个不同类型的编程问题，包括数据结构、图论、排序、链表操作、二分查找和集合操作等。
扫一扫
2643
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
