禁忌搜索算法求解考虑二维装箱的车辆路径问题

eternal1995

已于 2024-01-20 18:18:32 修改

阅读量1.2k

点赞数 27

文章标签：数学建模算法启发式算法

于 2024-01-20 18:17:05 首次发布

本文链接：https://blog.youkuaiyun.com/eternal1995/article/details/135719638

版权

作者简介：本人擅长运筹优化建模及算法设计，包括各类车辆路径问题、生产车间调度、二三维装箱问题，熟悉CPLEX和gurobi求解器

微信公众号：运筹优化与学习

如有运筹优化相关建模或代码定制需求，可通过微信公众号联系我们

前言

之前和大家介绍了二维装箱问题、考虑二维装箱的车辆路径问题（2L-VRP），本篇推文算是前几篇推文的综合体，将介绍如何用禁忌搜索算法求解考虑二维装箱的车辆路径问题。

禁忌搜索算法简介

禁忌搜索算法（Tabu Search，简称TS）起源于对于人类记忆功能的模仿，是一种元启发式算法。它从一个初始可行解出发，试探一系列的特定搜索方向，选择让特定的目标函数值提升最多的移动。

禁忌搜索的核心在于，在邻域搜索的基础上，通过设置禁忌表（tabu list）对已经历过的搜索过程信息进行记录，避免陷入局部最优解，同时利用藐视准则来解禁一些优秀的解。

算法求解思路

整体的求解框架如下图所示

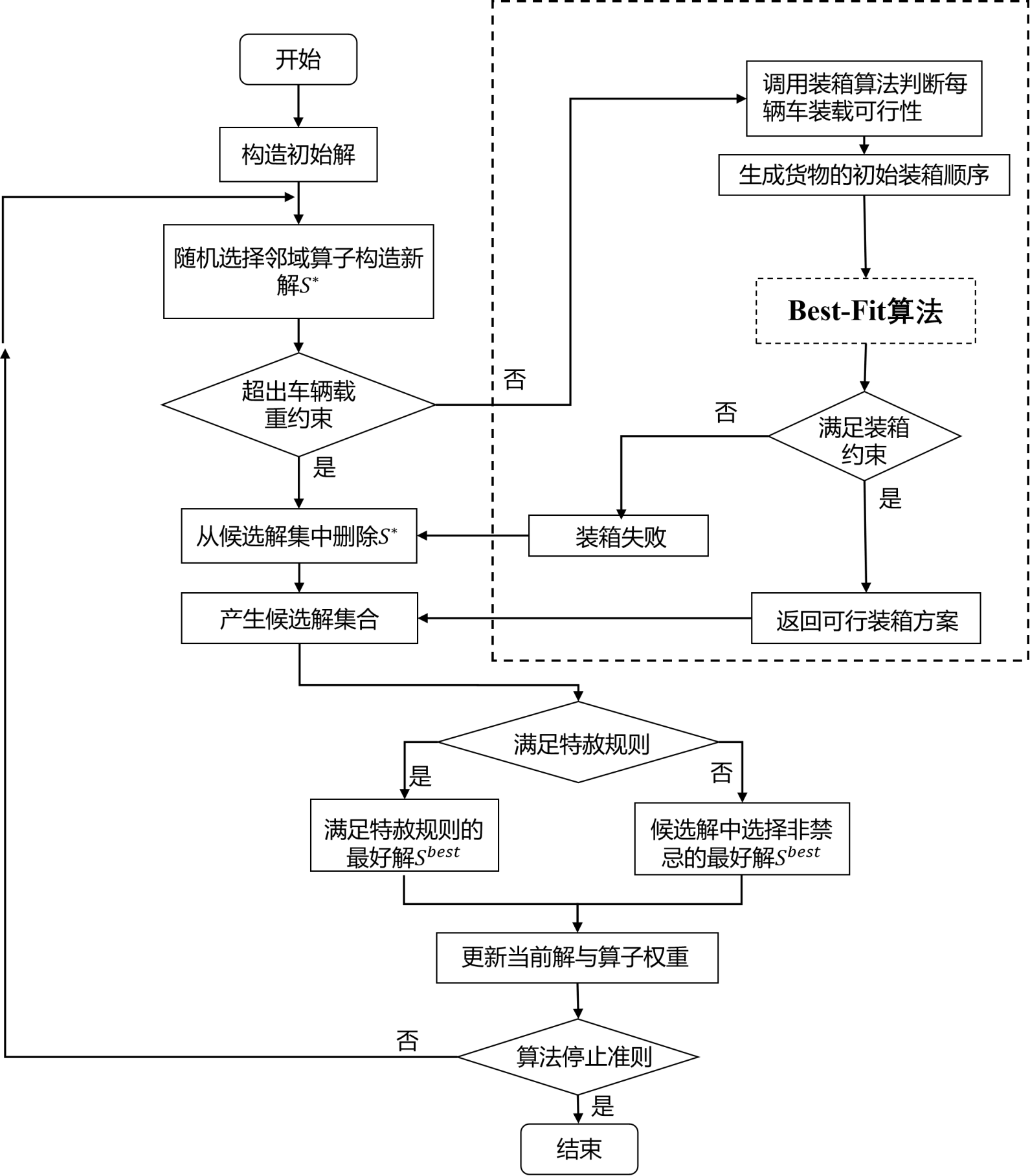
初始解构造

首先，给定 $K$ 辆空车，并根据物品表面积之和递减的原则将客户点排序。然后，客户节点按照给定的排序依次插入路径当中。对于每一个客户点 $(i = 1, 2, \dots, N)$ ，首先尝试将其插入到剩余装载面积最小的路径当中，这有助于最大化利用车辆的装载面积。如果存在这样一条路径，则将客户点插入到当前费用最小的位置上。

搜索算子

Intra-swap: 交换同一条路径当中的客户点位置。
Inter-swap: 交换不同路径当中的客户点位置。
Intra-shift: 将某一客户点从当前位置移除，并插入到该路径的另一位置。
Inter-shift: 将某一客户点从当前位置移除，并插入到另一路径的某一位置。
Intra-2opt: 对一给定路径，随机选择两不相邻的客户点，将两客户点之间的客户顺序全部逆序，其余客户点顺序不变。
Inter-2opt: 任意选择两条路径，将每条路径分成两部分，然后将一条路径的第一部分与另一条路径的第二部分连接起来，由此产生两条新的路径。若其中一条路径为空，则将另一条路径分成两条路径。

禁忌规则设置

禁忌长度（Tabu Tenure）：禁止在之后的n次迭代中对禁忌表中所记录的状态进行改变，这里的n即称为禁忌长度。
候选解（Candidate Solution）：当前邻域中的解。
藐视准则（Aspiration Criterion）：从候选解集合中挑选出最好的候选解，将其与当前最好解进行比较，若其是被禁止的解但是优于当前最好解，那么就将其解禁，用来作为下一迭代的当前解并及替代当前最好解，避免因为禁忌表而错过优异解的情况出现。

装箱算法

采用Best-Fit装箱算法，检验路径的装箱可行性，迭代过程中仅保留可行邻域解。装箱算法具体可见推文：

Best-Fit算法求解二维装箱问题

伪代码如下：

代码展示

%% 读取文件数据
data=importdata('2l_cvrp1301.txt');
dataset=textread('cvrp1302.txt');
Rectangle=read_rect(dataset);
cap=38000; %车辆负荷
vecnum=7;  %车辆数
bin_size.width=20;
bin_size.height=40;
vertexs=data(:,2:3);  %所有点的坐标x和y
customer=vertexs(2:end,:);%顾客坐标
cusnum=size(customer,1);  %顾客数
demands=data(2:end,4);  %需求量
h=pdist(vertexs);
dist=squareform(h);   %距离矩阵
for ii=1:cusnum
    Rectangle(ii).ID=ii;
    Rectangle(ii).x=0;
    Rectangle(ii).y=0;
    Rectangle(ii).width=1;
    Rectangle(ii).height=1;
end

%% 构造2LCVRP初始解
[init_vc] = Construct_init(customer,vecnum,Rectangle,demands,cap,bin_size,dist);
[init_vc] = Switch(init_vc);
S=init_vc;  %当前解                               
Sbest=S; %全局最优解
fBest=travel_distance(S,dist); 

%% Tabu Search
maxIter=1000;   %最大迭代次数
Iteration=0;
tabuList=[];
Tabu_tenure=10;  %禁忌表长度
[bCList,NeiborIndex] = SelectNeighbor(S,demands,dist,cap,Rectangle,bin_size);
[subNS]=subNeighbor(tabuList,bCList,fBest,Iteration,S);

融合禁忌搜索策略的装箱算法

%% 判断是否符合装载约束，若Ymax<=L,则满足装箱约束
function [ flag ]  = PackingTest(L,Rectangle,route)

Order = 3;
MaxIter = 15;
flag=0;
SumOfOrder=3;
Rects=[];
for cindex=1:length(route)
    customer=route(cindex);
    items=[Rectangle.ID]==customer;
    Rects = [Rects,Rectangle(items)];
end

while Order<=SumOfOrder
    Iter = 1;
    [ Array ] = Sort2( Rects,Order );
    rect_num = size(Array,2);
    Tabu=zeros(rect_num,rect_num);                                    %禁忌表
    TabuTenure=10;                                                    %禁忌长度
    while (Iter <= MaxIter)
        [Ymax,Array] = Best_Fit_Heuristic(Array);
        if (Ymax <= L) % if HeuristicPack plce all the rectangles, return success
            flag=1;
            return;
        else
            [ NS ] = Swap( Array );
            [subNS]=subNeighbor1(Tabu,NS,Ymax);
            if ~isempty(subNS)
                [~, minIndex] = min(subNS(:,3));
                value=subNS(minIndex,:);                       %提取最小行序号的这一行数组
                i=value(1);
                j=value(2);
                minY=value(3);
                if minY <= L
                    flag = 1;
                    return;
                else
                    flag = 0;
                    temp = Array(i);
                    Array(i) = Array(j);
                    Array(j) = temp;
                    Tabu(i,j)= TabuTenure;
                end
            else
                flag=0;
                return;
            end
        end
        Tabu=Tabu-1;
        Iter=Iter+1;
    end
    Order=Order+1;
end

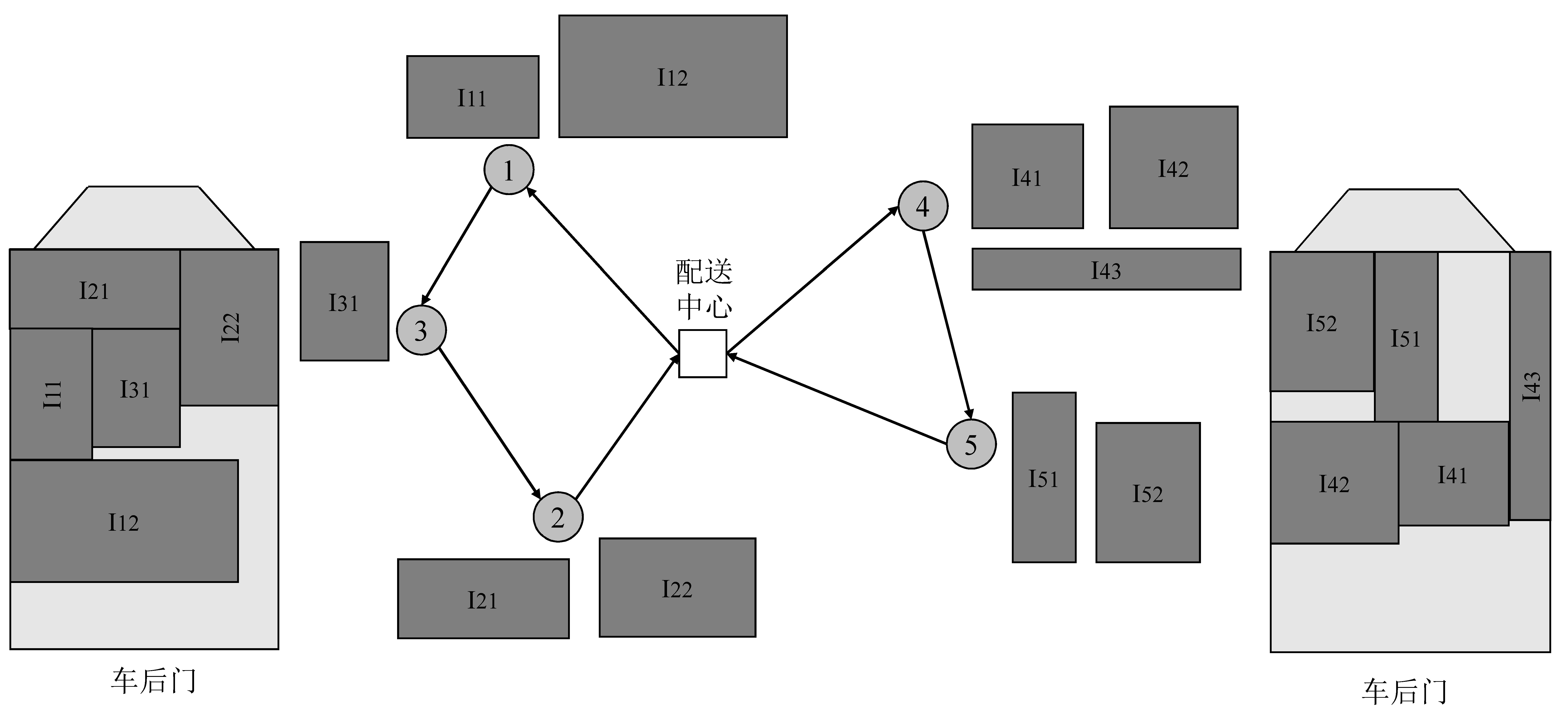
结果输出： 路径访问顺序、车辆的装载方案。

参考文献

[1]Gendreau, M., Iori, M., Laporte, G., & Martello, S. (2008). A tabu search heuristic for the vehicle routing problem with two-dimensional loading constraints. Networks,51(1), 4–18. 10.1002/net.20192

[2]Leung, S. C. H., Zhou, X., Zhang, D., & Zheng, J. (2011). Extended guided tabu search and a new packing algorithm for the two-dimensional loading vehicle routing problem. Computers & Operations Research, 38(1), 205–215. 10.1016/j.cor.2010.04.013

[3]张政.不确定环境下带二维装载约束的越库配送车辆路径问题研究[D].中南大学,2022.DOI:10.27661/d.cnki.gzhnu.2022.004738

若有运筹优化建模及算法定制需求，欢迎联系我们私聊沟通## 前言
之前和大家介绍了二维装箱问题、考虑二维装箱的车辆路径问题（2L-VRP），本篇推文算是前几篇推文的综合体，将介绍如何用禁忌搜索算法求解考虑二维装箱的车辆路径问题。