Acwing 848.有向图的拓扑序列

Acwing 848.有向图的拓扑序列

链接：848. 有向图的拓扑序列 - AcWing题库

/*
啥是拓扑排序?
首先要满足有向无环图的条件
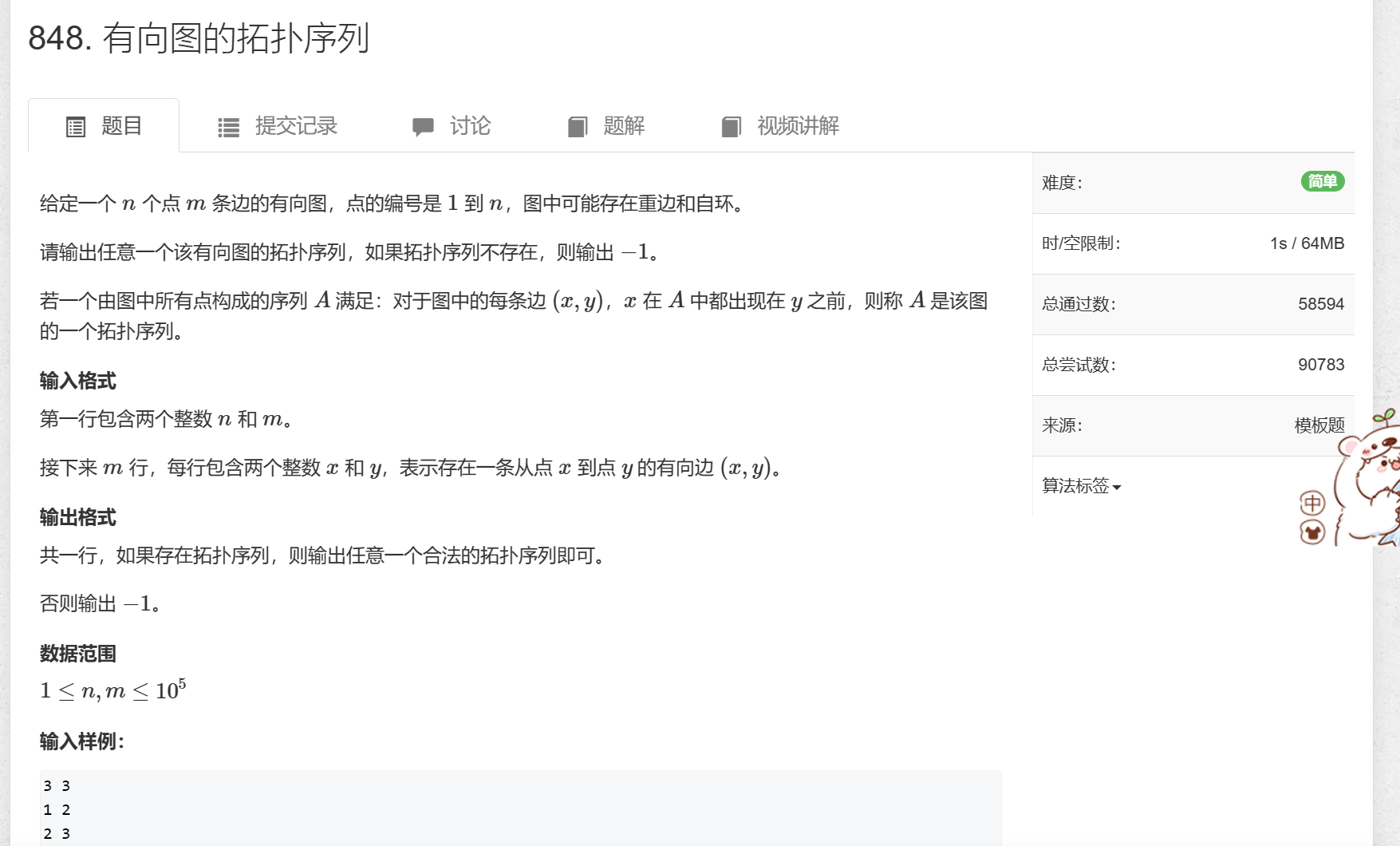
一个有向图，如果图中有入度为 0 的点，就把这个点删掉，同时也删掉这个点所连的边。
一直进行上面出处理，如果所有点都能被删掉，则这个图可以进行拓扑排序
题解:
bfs 将入度为0的节点加入队列 然后假设删除此节点
更改其他点的入度数 重复以上操作
如果出现环路bfs会提前结束 那么久可以判断是否所有节点都被加入过队列就行了

队列的出队顺序就是拓扑序列

*/
#include<iostream>
#include<cstring>
#include<algorithm>
#include<queue>

using namespace std;

const int N = 1e5+100;
int e[N],h[N],ne[N],idx;
int d[N];//保存点的入度数
int n,m;
int ans[N];
int cnt;

void add(int a,int b){
    e[idx]=b;
    ne[idx]=h[a];
    h[a]=idx++;
}

void topsort(){
    queue<int >que;
    for(int i=1;i<=n;i++){
        if(!d[i]){
            que.push(i);
            ans[++cnt] = i;
        }
    }
    while(!que.empty()){
        int t = que.front();
        // cout<<t<<endl;
        que.pop();
        for(int i = h[t];i!=-1;i=ne[i]){
            d[e[i]]--;
            if(!d[e[i]]){//入度的个数 也可以保证不会有重复的点加入队列 因为当这个点被加入到队列 就可以保证d[e[i]为0
                que.push(e[i]);
                ans[++cnt] = e[i];
            }
        }
    }
    if(n == cnt){
        for(int i=1;i<=cnt;i++){
            cout<<ans[i]<<" ";
        }
    }else{
        cout<<-1;
    }
    cout<<endl;
}
int main()
{
    cin>>n>>m;
    memset(h,-1,sizeof h);
    for(int i=0;i<m;i++){
        int a,b;
        cin>>a>>b;
        add(a,b);
        d[b]++;
    }
    topsort();
    return 0;
}