剑指Offer——JZ10 矩形覆盖

最新推荐文章于 2022-12-16 08:13:57 发布

原创最新推荐文章于 2022-12-16 08:13:57 发布 · 165 阅读

0 ·

CC 4.0 BY-SA版权

JZ 专栏收录该内容

17 篇文章

订阅专栏

该博客介绍了如何使用动态规划方法来解决一个数学问题：用n个21的小矩形无重叠地覆盖一个2*n的大矩形的不同方式数量。给出了当n等于1、2和4时的具体例子，并展示了一个动态规划实现的C++代码片段。动态规划算法通过维护前两个状态来计算当前状态的方法数，从而得出总的不同覆盖方式数。

描述

我们可以用21的小矩形横着或者竖着去覆盖更大的矩形。请问用n个21的小矩形无重叠地覆盖一个2*n的大矩形，从同一个方向看总共有多少种不同的方法？

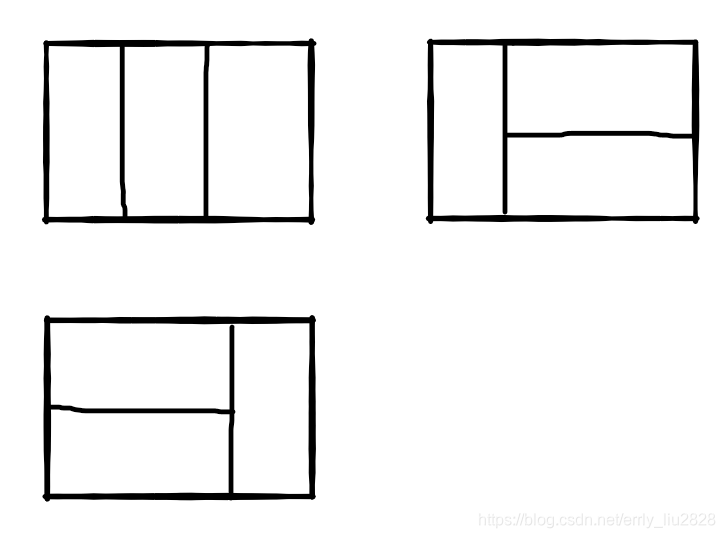
比如n=3时，2*3的矩形块有3种不同的覆盖方法(从同一个方向看)：
在这里插入图片描述

输入描述

2*1的小矩形的总个数n

返回值描述

覆盖一个2*n的大矩形总共有多少种不同的方法(从同一个方向看)

输入： 0
返回值： 0
输入： 1
返回值： 1
输入： 4
返回值： 5

class Solution {
public:
    int rectCover(int number) {
        if(number == 1 || number == 2)
            return number;
        int a = 1, b = 1, c;
        for(int i = 2; i<= number; i++){
            c = a+b;
            a = b;
            b = c;
        }
        return c;
    }
};