【JZOJ4671】World Tour

最新推荐文章于 2019-12-19 15:42:11 发布

原创最新推荐文章于 2019-12-19 15:42:11 发布 · 164 阅读

0 ·

CC 4.0 BY-SA版权

杂题同时被 3 个专栏收录

42 篇文章

订阅专栏

图论

28 篇文章

订阅专栏

最短路

24 篇文章

订阅专栏

本文介绍了一种寻找四个城市间最长旅行路径的方法，通过预处理两两点间距离并利用最远距离点来快速确定路径，适用于有限预算下的最优路径选择。

description

Cicasso是一个著名的雕塑家。
现在他想去城市之间旅游，他是一个聪明的人，所以从一个城市到另一个城市他只会走最短路。他想游览全国的风景，所以他想走的路的总长度尽量长，但是经费有限，他只能去四个城市，而且这四个城市不能重复（在途中经过的城市不计算，例如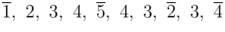，他要去的四个城市有上标，[1, 5, 2, 4]，这样是合法的）
注意，道路是单向路，并且距离都为1。

analysis

首先可以用 $n$ 个 $S P F A$ 来预处理两两点间的距离
然后可以 $O(n^2)$ 预处理 $x$ 号点最远到达的两个点和逆着走走到 $x$ 号点的某两个最远的点
四个城市，只需枚举中间的两个，然后由前面那个最远两个就可以很快地知道剩下两个城市

code

#pragma GCC optimize("O3")
#pragma G++ optimize("O3")
#include<stdio.h>
#include<string.h>
#include<algorithm>
#include<queue>
#define MAXN 3005
#define MAXM 5005
#define INF 1000000007
#define ll long long
#define reg register ll
#define max(x,y) (x>y?x:y)
#define min(x,y) (x<y?x:y)
#define fo(i,a,b) for (reg i=a;i<=b;++i)
#define fd(i,a,b) for (reg i=a;i>=b;--i)
#define rep(i,a) for (reg i=last[a];i;i=next[i])
#define O3 __attribute__((optimize("-O3")))

using namespace std;

ll last[MAXM],next[MAXM],tov[MAXM];
ll dis[MAXN][MAXN];
ll f[MAXN][2],g[MAXN][2];
bool bz[MAXN];
ll n,m,tot;
queue<ll>que;

O3 inline ll read()
{
	ll x=0,f=1;char ch=getchar();
	while (ch<'0' || '9'<ch){if (ch=='-')f=-1;ch=getchar();}
	while ('0'<=ch && ch<='9')x=x*10+ch-'0',ch=getchar();
	return x*f;
}
O3 inline void link(ll x,ll y)
{
	next[++tot]=last[x],last[x]=tot,tov[tot]=y;
}
O3 inline bool judge(ll a,ll b,ll c,ll d)
{
	return a!=b && a!=c && a!=d && b!=c && b!=d && c!=d;
}
O3 int main()
{
	//freopen("World Tour.in","r",stdin);
	n=read(),m=read();
	fo(i,1,m){ll x=read(),y=read();link(x,y);}
	fo(k,1,n)
	{
		while (!que.empty())que.pop();
		memset(dis[k],-1,sizeof(dis[k]));
		memset(bz,1,sizeof(bz));
		que.push(k),dis[k][k]=bz[k]=0;
		while (!que.empty())
		{
			ll now=que.front();que.pop(),bz[now]=1;
			rep(i,now)if (dis[k][tov[i]]==-1)
			{
				dis[k][tov[i]]=dis[k][now]+1;
				if (bz[tov[i]])bz[tov[i]]=0,que.push(tov[i]);
			}
		}
	}
	fo(i,1,n)
	{
		f[i][0]=f[i][1]=g[i][0]=g[i][1]=i;
		fo(j,1,n)
		{
			if (dis[i][j]>dis[i][f[i][0]])f[i][1]=f[i][0],f[i][0]=j;
			else if (dis[i][j]>dis[i][f[i][1]])f[i][1]=j;
			if (dis[j][i]>dis[g[i][0]][i])g[i][1]=g[i][0],g[i][0]=j;
			else if (dis[j][i]>dis[g[i][1]][i])g[i][1]=j;
		}
	}
	ll ans=-1,ans1,ans2,ans3,ans4;
	fo(i,1,n)fo(j,1,n)if (i!=j && dis[i][j]!=-1)
	fo(k,0,1)fo(l,0,1)
	{
		ll x=g[i][k],y=f[j][l];
		if (judge(x,i,j,y) && dis[x][i]+dis[i][j]+dis[j][y]>ans)
		ans=dis[x][i]+dis[i][j]+dis[j][y],ans1=x,ans2=i,ans3=j,ans4=y;
	}
	printf("%lld %lld %lld %lld\n",ans1,ans2,ans3,ans4);
	return 0;
}