【luoguP1099】【NOIP2007】树网的核

description

 设T=(V, E, W) 是一个无圈且连通的无向图（也称为无根树），每条边带有正整数的权，我们称T为树网（treenetwork），其中V, E分别表示结点与边的集合，W表示各边长度的集合，并设T有n个结点。

    路径：树网中任何两结点a,b都存在唯一的一条简单路径，用d(a,b)表示以a,b为端点的路径的长度，它是该路径上各边长度之和。我们称d(a,b)为a,b两结点间的距离。

    一点v到一条路径P的距离为该点与P上的最近的结点的距离：

                    d(v，P)=min{d(v，u)，u为路径P上的结点}。
                    
    树网的直径：树网中最长的路径称为树网的直径。对于给定的树网T，直径不一定是唯一的，但可以证明：各直径的中点（不一定恰好是某个结点，可能在某条边的内部）是唯一的，我们称该点为树网的中心。

    偏心距ECC(F)：树网T中距路径F最远的结点到路径F的距离，即

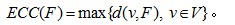
    任务：对于给定的树网T=(V, E,W)和非负整数s，求一个路径F，它是某直径上的一段路径（该路径两端均为树网中的结点），其长度不超过s（可以等于s），使偏心距ECC(F)最小。我们称这个路径为树网T=(V,E,W)的核（Core）。必要时，F可以退化为某个结点。一般来说，在上述定义下，核不一定只有一个，但最小偏心距是唯一的。

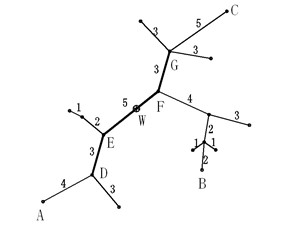
    下面的图给出了树网的一个实例。图中，A-B与A-C是两条直径，长度均为20。点W是树网的中心，EF边的长度为5。如果指定s=11，则树网的核为路径DEFG（也可以取为路径DEF），偏心距为8。如果指定s=0（或s=1、s=2），则树网的核为结点F，偏心距为12。

---

analysis

• 正解floyd+枚举

• 数据太小了，最长路可以直接$floydO(n^3)$求出来，再$O(n^3)$预处理在直径（最长路）上的点

• 然后$O(n^2)$枚举一条长度不超过$s$的路径，$O(n)$枚举在这条路径上的边，再一个$O(n)$枚举统计答案

• 时间复杂度$O(n^4)$…

---

code

#pragma GCC optimize("O3")
#pragma G++ optimize("O3")
#include<stdio.h>
#include<string.h>
#include<algorithm>
#define MAXN 305
#define INF 1000000007
#define ll long long
#define reg register ll
#define fo(i,a,b) for (reg i=a;i<=b;++i)
#define fd(i,a,b) for (reg i=a;i>=b;--i)
#define O3 __attribute__((optimize("-O3")))

using namespace std;

ll a[MAXN][MAXN],f[MAXN][MAXN];
bool bz[MAXN];
ll c[MAXN];
ll n,s,mx,tot,ans=INF;

O3 inline ll read()
{
	ll x=0,f=1;char ch=getchar();
	while (ch<'0' || '9'<ch){if (ch=='-')f=-1;ch=getchar();}
	while ('0'<=ch && ch<='9')x=x*10+ch-'0',ch=getchar();
	return x*f;
}
O3 inline ll max(ll x,ll y)
{
	return x>y?x:y;
}
O3 inline ll min(ll x,ll y)
{
	return x<y?x:y;
}
O3 int main()
{
	freopen("core.in","r",stdin);
	freopen("core.out","w",stdout);
	n=read(),s=read();
	memset(a,60,sizeof(a));
	fo(i,1,n)a[i][i]=0;
	fo(i,1,n-1)
	{
		ll x=read(),y=read();
		a[x][y]=a[y][x]=read();
	}
	fo(k,1,n)
	{
		fo(i,1,n)
		{
			fo(j,1,n)
			if (a[i][j]>a[i][k]+a[k][j])
			{
				a[i][j]=a[i][k]+a[k][j];
				mx=max(mx,a[i][j]);
			}
		}
	}
	fo(i,1,n)
	{
		fo(j,1,n)if (a[i][j]==mx)
		{
			fo(k,1,n)bz[k]=(a[i][k]+a[k][j]==mx);
		}
	}
	fo(i,1,n)
	{
		fo(j,i,n)if (bz[i] && bz[j] && a[i][j]<=s)
		{
			memset(c,60,sizeof(c)),tot=0;
			fo(k,1,n)if (a[i][k]+a[k][j]==a[i][j])
			{
				fo(l,1,n)
				if (a[k][l]<c[l])c[l]=a[k][l];
			}
			fo(k,1,n)tot=max(tot,c[k]);
			ans=min(ans,tot);
		}
	}
	printf("%lld\n",ans);
	return 0;
}