【JZOJ3766】【luoguP4219】【BJOI2014】大融合

最新推荐文章于 2019-12-19 15:42:11 发布

原创最新推荐文章于 2019-12-19 15:42:11 发布 · 345 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#lct #杂题

杂题同时被 2 个专栏收录

42 篇文章

订阅专栏

LCT

11 篇文章

订阅专栏

本文介绍了一种在线处理通信系统中动态变化的边负载查询的方法。通过使用链剖分技术及线性时间复杂度的链查找树（LCT），实现了在增加边的同时快速更新负载并响应查询。

problem

Description

小强要在N个孤立的星球上建立起一套通信系统。这套通信系统就是连接N个点的一个树。这个树的边是一条一条添加上去的。在某个时刻，一条边的负载就是它所在的当前能够联通的树上路过它的简单路径的数量。

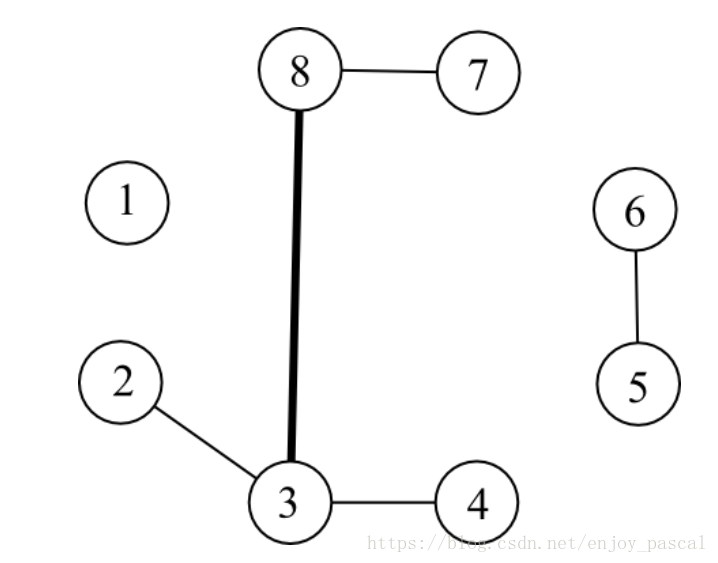
例如，在上图中，现在一共有了5条边。其中，(3,8)这条边的负载是6，因为有六条简单路径2-3-8,2-3-8-7,3-8,3-8-7,4-3-8,4-3-8-7路过了(3,8)。

现在，你的任务就是随着边的添加，动态的回答小强对于某些边的负载的询问。

Input

第一行包含两个整数N,Q，表示星球的数量和操作的数量。星球从1开始编号。

接下来的Q行，每行是如下两种格式之一：

A x y 表示在x和y之间连一条边。保证之前x和y是不联通的。

Q x y 表示询问(x,y)这条边上的负载。保证x和y之间有一条边。

Output

对每个查询操作，输出被查询的边的负载。

Sample Input

8 6

A 2 3

A 3 4

A 3 8

A 8 7

A 6 5

Q 3 8

Sample Output

Data Constraint

对于40%的数据，N,Q≤1000

对于100%的数据，1≤N,Q≤100000

analysis

在线LCT维护子树大小，离线算法可以用树剖~~（不讲）~~
经过 $(x,y)$ 这条边的路径数量就是 $x$ 一边子树大小乘上 $y$ 一边子树大小
对于 $link$ ，除了普通操作我们还要 $makeroot(y)$ ，然后 $size[y]+=size[x]$ ，方便更新 $size$
而在 $rotate$ 之前也需要更新一次 $size$
对于询问，把 $x$ 旋到 $LCT$ 的根，把 $y$ 旋到 $x$ 的儿子节点
那么 $x$ 的子树大小为 $size[x]-size[y]$ ， $y$ 的子树大小就为 $size[y]$

code

#include<bits/stdc++.h>
#define MAXN 100001
#define fo(i,a,b) for (int i=a;i<=b;i++)

using namespace std;

int t[MAXN][2];
int fat[MAXN],fa[MAXN],pf[MAXN],st[MAXN];
int n,m;

struct node 
{
    int size;
    bool rev;
}a[MAXN];

int read()
{
    int x=0,f=1;
    char ch=getchar();
    while (ch<'0' || '9'<ch)
    {
        if (ch=='-')f=-1;
        ch=getchar();   
    }
    while ('0'<=ch && ch<='9')
    {
        x=x*10+ch-'0';
        ch=getchar();
    }
    return x*f;
}

void reverse(int x)
{
    if(x)
    {
        a[x].rev^=1;
        swap(t[x][0],t[x][1]);
    }
}

void down(int x)
{
    if (a[x].rev)
    {
        reverse(t[x][0]),reverse(t[x][1]);
        a[x].rev=0;
    }
}

void update(int x)
{
    if (x)
    {
    }
}

void downdata(int x)
{
    st[0]=0;
    while (x)st[++st[0]]=x,x=fa[x];
    while (st[0])down(st[st[0]--]);
}

int lr(int x)
{
    return t[fa[x]][1]==x;
}

void rotate(int x)
{
    int y=fa[x],k=lr(x);
    int temp=a[y].size-a[x].size;
    a[y].size=temp+a[t[x][!k]].size;
    a[x].size+=temp;

    t[y][k]=t[x][!k];

    if (t[x][!k])fa[t[x][!k]]=y;
    fa[x]=fa[y];

    if (fa[y])t[fa[y]][lr(y)]=x;
    t[x][!k]=y;

    fa[y]=x,pf[x]=pf[y];
    update(y),update(x);
}

void splay(int x, int y)
{
    downdata(x);
    while (fa[x]!=y)
    {
        if (fa[fa[x]]!=y)
        {
            if (lr(x)==lr(fa[x]))rotate(fa[x]); 
            else rotate(x);
        } 
        rotate(x);
    }
}

void access(int x)
{
    for (int y=0;x;update(x),y=x,x=pf[x])
    {
        splay(x,0);
        fa[t[x][1]]=0;
        pf[t[x][1]]=x;
        t[x][1]=y;
        fa[y]=x;
        pf[y]=0;
    }
}

void makeroot(int x)
{
    access(x);
    splay(x,0);
    reverse(x);
}

void link(int x,int y) 
{
    makeroot(x);
    makeroot(y);
    pf[x]=y;
    a[y].size+=a[x].size;
    update(y);
}

int main()
{
    //freopen("readin.txt","r",stdin);
    n=read(),m=read();
    fo(i,1,n)a[i].size=1;
    while (m--)
    {
        char ch=getchar();
        while (ch!='A' && ch!='Q')ch=getchar();
        int x=read(),y=read();
        if (ch=='A')link(x,y);
        else 
        {
            makeroot(x);
            access(y);
            splay(x,0);
            splay(y,x);
            printf("%lld\n",(long long)(a[x].size-a[y].size)*a[y].size);
        }
    }
    return 0;
}