【JZOJ3446】三角阵(tri)

problem

Description

把3个相同的小三角形按如下方式连接起来就形成了一个一级三角阵。

我们把位于顶端的小三角形标记为T，位于左端的小三角形标记为L，位于右端的小三角形标记为R。

把3个一级三角阵按同样的方式连接起来就形成了一个二级三角阵。

我们为顶端的三角阵的标记添加前缀T，为左端的三角阵的标记添加前缀L，为右端的三角阵的标记添加前缀R。

把3个二级三角阵按同样的方式连接起来就形成了一个三级三角阵。

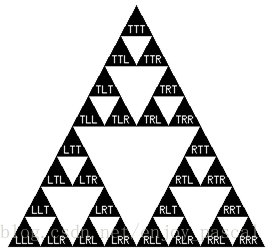
同样地为顶端的三角阵的标记添加前缀T，为左端的三角阵的标记添加前缀L，为右端的三角阵的标记添加前缀R。

依次类推，可以构建一个N级三角阵。

如果两个小三角形有公共点，则认为这两个小三角形相邻，可以一步到达。

你的任务是求从一个小三角形走到另一个小三角形至少需要多少步。

Input

第一行是三角阵的等级Ｎ（Ｎ≤30）。

第二行和第三行都是一个长度为N的字符串，由大写字母“L”、“R”、“T”组成，表示两个小三角形的标号。

Output

输出一个数，表示从一个小三角形走到另一个小三角形所需的最少步数。

Sample Input

3

TRL

RLR

Sample Output

5

【样例解释】

从“TRL”出发，途经“TRR”、“RTT”、“RTL”、“RLT”，最后到达“RLR”，一共需要5步。

Data Constraint

40% n<=5

100% n<=30

---

analysis

• 很明显地发现走步的数量和$2$的幂有关

• 设第