面向MIMO-OFDM的低功耗FFT设计

面向MOMO‐OFDM的面积高效低功耗MOD‐R2MDC快速傅里叶变换的超大规模集成电路设计与研究

1. 引言

多输入多输出正交频分复用（MIMO‐OFDM）是一种用于长距离传输和接收数据的高效解决方案。在我们提出的 MIMO‐OFDM收发器中，子载波频率的选择消除了子信道之间的串扰，因此无需使用载波间保护带[1]。这极大地简化了发射机和接收端的设计；与传统频分复用不同，无需为每个子信道单独配置滤波器[2]。正交性使得可以利用快速傅里叶变换（FFT）算法高效地实现调制器和解调器[3]。如今，OFDM收发器通过无线通信系统中的低成本MIMO‐OFDM被广泛应用于宽带通信。它要求接收端具有非常精确的频率同步，并且降低了系统复杂度[4]。在发射机中，若存在频率偏移，子载波将不再保持正交，从而引起符号间干扰[5]。此时，5/6编码速率将无法有效支持维特比译码器进行纠错[6]。本文描述了为MIMO‐OFDM系统提出的改进型基‐2多路径延迟交换（MOD‐R2MDC）的超大规模集成电路（VLSI）实现，即基于MOD‐R2MDC流水线FFT的MIMO‐OFDM系统。该基‐2算法采用多延迟交换架构，支持4通道8、16、32、64、128、512、1024和2048点FFT运算[7, 8]。我们将所提出的架构与现有的8点基‐2、基‐4FFT以及现有的R2MDC FFT进行了比较，并给出了所提出的MOD‐R2MDC FFT处理器的设计与实现结果。

2. 多输入多输出正交频分复用概述

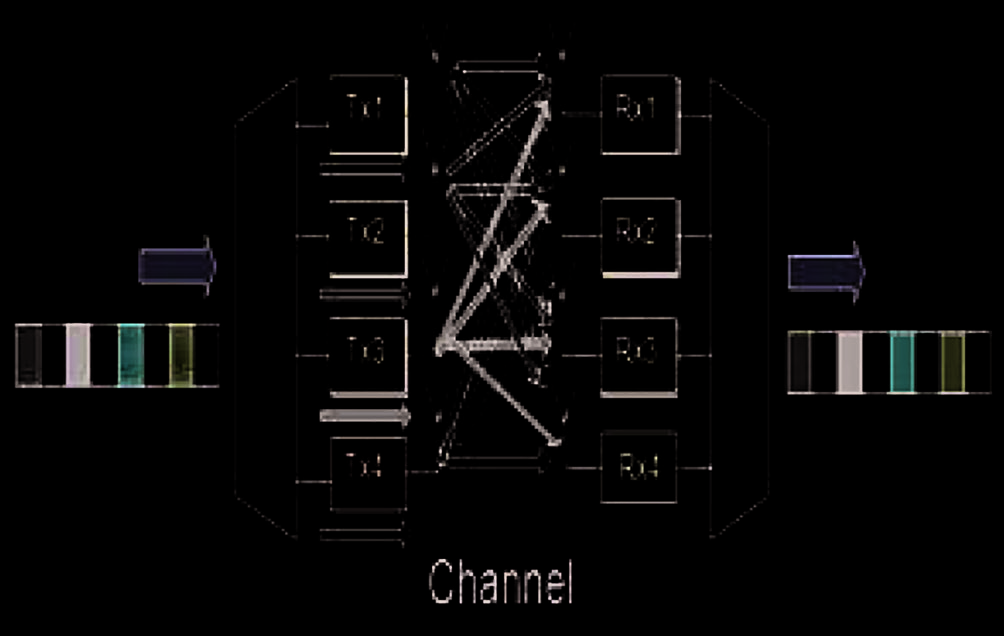
图1展示了多输入多输出正交频分复用的通用收发器结构。该系统由N个发射天线和M个接收天线组成。根据[9]和[10],，假设循环前缀长于信道时延扩展。每个天线的OFDM信号通过逆快速傅里叶变换获得，并可通过快速傅里叶变换进行检测。

目前有两种广泛使用的方法用于传输MIMO数据。如果信道具有可忽略的误码率，我们可以通过多个天线同时发送多个数据。这称为空间复用，能够高效利用频谱。

相比之下，如果环境误码率较高，我们通过多个天线传输相同的数据，这称为空时编码。该方法的目的是提高多输入多输出系统的分集增益，以对抗信号衰落。多输入多输出系统的核心任务是在接收端确定每个天线对应的数据。如图1所示，R×1从所有发射天线T×1、T×2、T×3和T×4接收数据。因此，我们必须采用特殊的解码算法来识别哪个天线向R×1发送了哪些数据。N×M 多输入多输出正交频分复用：其中N表示发射天线数量，M表示接收天线数量。例如，4×4多输入多输出正交频分复用系统具有四个发射天线和四个接收天线，如图1所示。

正交频分复用是一种多载波系统，其中数据比特被编码到多个子载波上。与单载波系统不同，所有频率同时在时间上发送。正交频分复用与单载波系统相比，正交频分复用具有更好的多径效应免疫性、更简单的信道均衡以及更宽松的定时获取约束。然而，它对本地频率偏移和射频前端非线性更为敏感[11]。正交频分复用系统中使用的频率是正交的，因此可以使用具有重叠频谱的相邻频率[12]。

3. 逆快速傅里叶变换/快速傅里叶变换算法

本节简要概述了逆快速傅里叶变换和FFT算法，以便在正交频分复用应用中有效使用。N点离散快速傅里叶变换（DFT）定义为：

(1)
where is the DFT coefficient.
X(k) 是第k次谐波，x(n) 是第n个输入样本。直接计算DFT需要O(N²)的计算复杂度。通过使用库利‐图基快速傅里叶变换算法，复杂度可降低至O(N logᵣ N)。由于可以对任意N进行因数分解，库利‐图基快速傅里叶变换是所有FFT算法中最通用的一种。

Cooley‐Tukey算法基于频域中的分治法，因此被称为频域抽取FFT。DFT公式被分为两个求和式：
and
(2)
X[k]可以抽样为偶数和奇数索引频率样本：
(3)
(4)
通过将N/2点DFT X(2k)和DFT X(2K+1)进行抽取，该计算过程可以重复进行。整个算法包含log₂N个阶段，每个阶段包含N/2个运算单元（蝶形）。如时间抽取算法一样，通过DIF快速傅里叶变换计算N点DFT需要(N/2).log₂N次复数乘法和N.log₂N次复数加法[13]。

4. 提出的改进型基‐2多路延迟交换架构

基‐2蝶形处理器由一个复数加法器和复数减法组成。此外，还实现了一个用于旋转因子W N 的额外复数乘法器。如图2所示，与旋转因子的复数乘法需要四次实数乘法和两次加/减运算。

改进型基2多路径延迟交换是基2 FFT算法的一种交换结构，用于尽可能快地交换数值以处理数据并交换FFT输入。图3所示的架构由多个不同的模块组成，这些模块必须在改进型基2多路径延迟交换中使用。

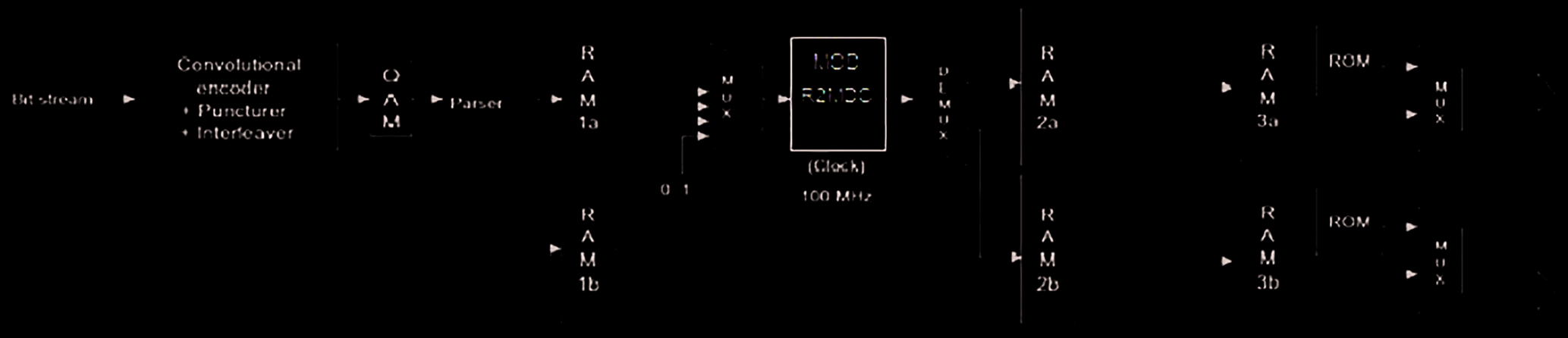
实现R2 FFT算法流水线的最直接方法之一是 MOD‐R2MDC架构。这是对FFT/IFFT算法进行数据重排的最简单方式，输入数据序列被分解为两路并行数据流向前流动，通过适当的延迟 [14] 调度进入蝶形运算的数据元素保持正确的间距。在 MOD‐R2MDC 架构的 8点FFT 每一级中，一半的数据流通过存储器（寄存器）进行延迟，并与另一半数据流 [15] 进行处理。

A输入来自前一个组件旋转因子乘法器。B输出被送至下一个组件，通常为蝶形结构II（BF II）。在初始周期中，多路复用器将输入数据引导至反馈寄存器，直到它们填满（位置“0”）。在接下来的周期中，多路复用器选择加法器或减法器的输出（位置“1”），蝶形运算单元利用输入数据和反馈寄存器中存储的数据执行2点DFT。支持两条接收链的BF I和BF II架构如图4(a)和4(b)所示。

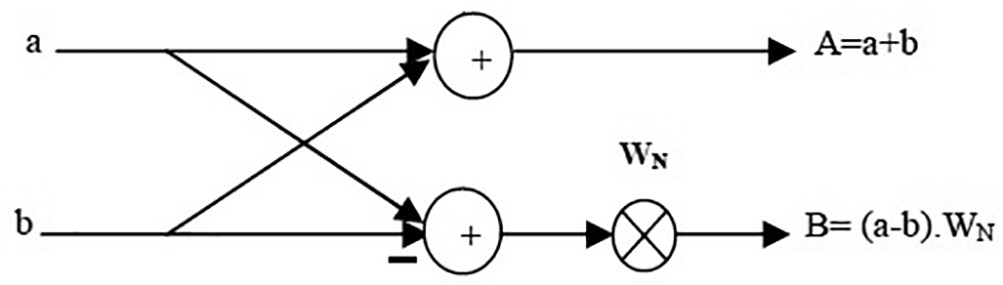
在BF I结构中，蝶形随机存取存储器（BF‐RAMs）的输入和输出端的样本路由多路复用器及解复用器由c2和c3控制信号控制，而计算单元则由c1控制信号控制。根据接收链数量的配置，额外的BF‐RAM被启用。根据需求，可在现有BF结构上扩展额外的缓冲区。由于−1,+j和−j的乘法运算在BF II结构内部处理，因此基本计算单元使用两个控制信号c1和c2。多路复用器和解复用器由c3和c4控制信号控制。“−j”项的乘积通过交换实部和虚部并考虑样本符号来实现。此处采用的算法是在IFFT架构[2]中换位R2算法。

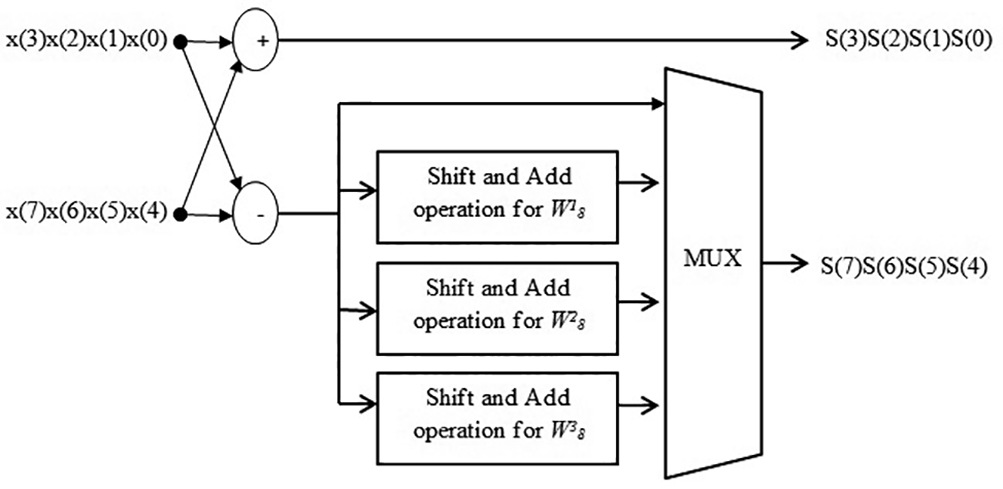
为了优化处理器，所提出的移位相加法消除了与旋转因子（W₈¹, W₈³）的非平凡复数乘法，从而实现了无需复数乘法的处理器。所提出的蝶形处理器通过将实部切换到虚部、虚部切换到实部来完成与平凡因子W₈² = −j的乘法运算，而因子W₈⁰则通过简单的连线实现。对于非平凡因子W₈¹ = e⁻ʲᵖⁱ/⁴和W₈³ = e⁻ʲ³ᵖⁱ/⁴，处理器通过图5所示的硬连线移位/加法操作实现1/√2因子的乘法运算。

5. 结果与讨论

主要目标是构建一种具有低功耗和更小面积的快速傅里叶变换（FFT）。在将所提出的电路与其他FFT进行比较时，充分考虑了（i）功耗和（ii）面积占用这两个参数。实验结果分析包括六种不同类型的架构，即基2（R2）、基4（R4）、分裂基（spilt radix）、混合R4/2、R2MDC和改进型基2多路径延迟交换快速傅里叶变换（MOD R2MDC FFT），这些架构均可在Altera Cyclone II 开发与教育平台2（DE2）现场可编程门阵列（FPGA）上实现。我们使用硬件描述语言完成了所有编码设计。

为了获得功耗和面积报告，采用XILINX ISE 设计套件10.1作为综合工具，并使用Modelsim 6.3c进行仿真。该设计的目的在于确定资源使用情况，尝试消除复数乘法，从而避免这一高成本的乘法操作，并减少芯片面积的占用。如表1所示，所提出的改进型基‐2实数快速傅里叶变换（MOD‐R2MDC FFT）在面积和功耗方面均优于基2 FFT和现有的R2MDC FFT。

各种FFT算法的仿真结果已通过在Altera DE‐2 FPGA开发板上实际实现进行了测试。使用Quartus‐II工具将设计下载到 FPGA开发板中。在FPGA板上，复位信号输入连接至最右侧的开关。通过其余开关设置二进制输入后，在FPGA处理完成后，输出结果可在开发板的发光二极管显示上观察到。此外，这些FPGA输出结果可通过Modelsim 6.3c获得的仿真结果进行验证。该FPGA板已用于验证电路行为以及在无线通信系统中实现MIMO‐OFDM。

方法	切片	查找表	功耗（瓦）
改进型基2多路径延迟交换	149	145	0.47
基2多路径延迟交换	197	152	1.103
基2	320	432	2.179

表1：所提出的改进型基2多路径延迟交换快速傅里叶变换与现有基2多路径延迟交换和基2架构的比较结果

6. 结论

在此工作中，使用超大规模集成电路设计流程设计了多种快速傅里叶变换算法，如基2、基2多路径延迟交换和所提出的改进型基2多路径延迟交换快速傅里叶变换，并对其性能进行了分析。从结果中可以看出，所提出的改进型基2多路径延迟交换快速傅里叶变换使用最少数量的可配置逻辑块切片，节省了约10%的面积，并且与其它FFT相比功耗仅消耗<20%。可以看出，新的 MOD‐R2MDC FFT算法提供了更小面积和低功耗。超高速集成电路硬件描述语言的仿真结果已在Altera DE‐2 FPGA开发板上实际实现并进行了测试。同时，现有的OFDM系统也采用这些FFT算法进行了测试，并对其在FPGA中所占面积和功耗方面的性能进行了分析。我们得出结论：所提出的 MOD‐R2MDC架构占据的面积更小，消耗的功耗低于现有的 R2和R2MDC FFT算法架构。该架构表明其可用于无线通信系统中的MIMO‐OFDM等低功耗应用。