C++_二叉搜索树

目录

1、二叉搜索树的概念

 2、二叉搜索树的插入

3、二叉搜索树的查找

4、二叉搜索树的删除

5、二叉搜索树的拷贝构造与析构

---

前言：

        二叉搜索树是一颗二叉树，他跟普通的二叉树的区别在于：二叉搜索树的节点是按照特定规则进行摆放的。二叉搜索树的优势在于：无特殊情况下，其增删查改数据的时间复杂度可以达到O(log N)，这个效率相比于线性表的效率，前者明显高出很多。

1、二叉搜索树的概念

        二叉搜索树具备搜索功能的同时还可以通过中序遍历进行排序，因此二叉搜索树也称二叉排序树。他的具体性质如下：

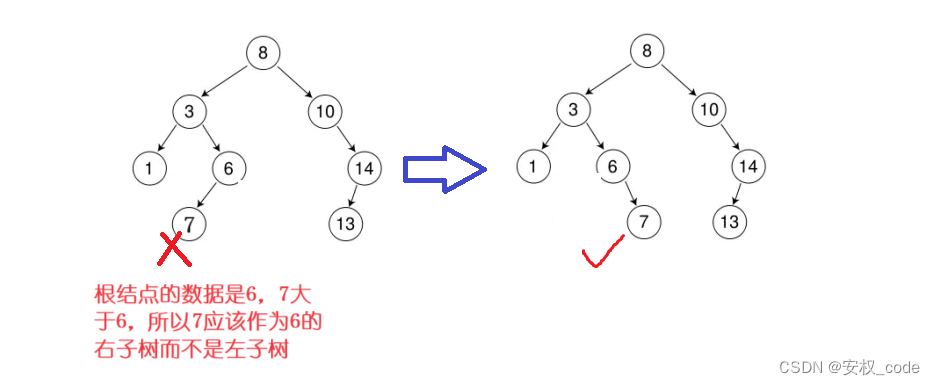
1、左子树所有节点的值都小于根节点的值。

2、右子树所有节点的值都大于根节点的值。

3、左子树和右子树本身也同样满足上面两个性质。

4、树中不能出现相同值的节点。

        二叉搜索树示意图如下：

 2、二叉搜索树的插入

        若要插入新的节点，则需遵循二叉树的性质，若插入节点的数值比根结点大则往右子树遍历，若插入节点的数值比根结点小则往左子树遍历，如此反复遍历，直到遇到nullptr，说明已经走到了插入点的位置，插入的时候还需要把该节点和父节点进行连接。若插入的数据和树里数据相同，则不能插入。

         插入代码如下：

#define _CRT_SECURE_NO_WARNINGS 1

#include<iostream>
using namespace std;

template<class K>
struct BSTree_node//节点对象
{
	BSTree_node<K>* left;
	BSTree_node<K>* right;
	K key;

	BSTree_node(const K& k)
		:left(nullptr)
		, right(nullptr)
		, key(k)
	{}
};

template<class K>
class BSTree//树对象
{
public:
	typedef BSTree_node<K> node;

	void _Insert(const K& k)//子函数，方便外部调用
	{
		Insert(_root, k);
	}
	bool Insert(node*& root, const K& k)//递归实现插入函数
	{
		if (root == nullptr)//找到空处，因为root是引用，因此可以直接插入新节点
		{
			root = new node(k);
			return true;
		}

		//按照左边找小，右边找大遍历树
		if (k > root->key)
		{
			Insert(root->right, k);
		}
		else if (k < root->key)
		{
			Insert(root->left, k);
		}
		else//相同则不会插入
			return false;
	}

	//打印函数
	void _show()
	{
		show(_root);
	}
	void show(node* root)//中序遍历打印
	{
		if (root == nullptr)
		{
			return;
		}

		show(root->left);
		cout << root->key << " ";
		show(root->right);
	}

private:
	node* _root = nullptr;
};