动态规划01机器人走K步到达aim的方法数

题目：

假设有排成一行的N个位置记为1~N，N一定大于或等于2

开始时机器人在其中的M位置上(M一定是1~N中的一个)

如果机器人来到1位置，那么下一步只能往右来到2位置；

如果机器人来到N位置，那么下一步只能往左来到N-1位置；

如果机器人来到中间位置，那么下一步可以往左走或者往右走；

规定机器人必须走K步，最终能来到P位置(P也是1~N中的一个)的方法有多少种

给定四个参数 N、M、K、P，返回方法数

参数分析：

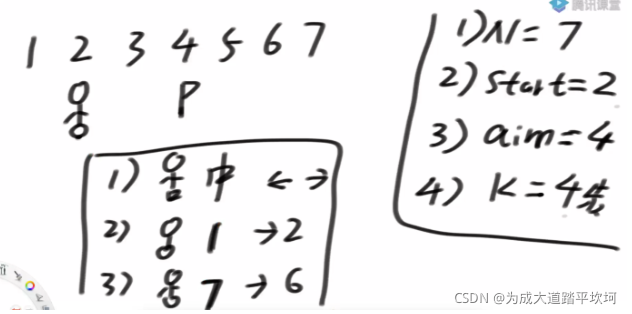
• N表示一共7个数
• start表示机器人的起始位置在2
• aim表示机器人的目标位置在4
• k表示需要走的步数

机器人的运动规则：

• 在中间位置，机器人可左可右
• 在1位置，只能往2位置移动
• 在N位置，只能往N-1位置移动

暴力递归解法

1. 先写递归函数，递归函数的参数：当前位置cur、剩余步数rest、路径长度N、目标位置aim，返回值为方法数
2. 在主函数中调用这个函数，填入对应的实参。
3. 递归函数的basecase，剩余步数为0；
4. 运动情况分析，cur位于左边界，cur位于右边界，cur位于中间位置。

//设置尝试函数
//cur为当前位置
//rest 为剩余步数
//N为路径长度
//aim为目标位置
int process(int cur, int rest,int N,int aim) {
	if (rest == 0) {
		return cur == aim ? 1 : 0;
	}
	if (cur == 1) {
		return process(2, rest - 1, N, aim);
	}
	if (cur == N) {
		return process(N - 1, rest - 1, N, aim);
	}
	return process(cur - 1, rest - 1, N, aim) + process(cur + 1, rest - 1, N, aim);
}
//暴力递归法
int way1(int N, int start, int aim, int K) {
	if (start<1 || start>N || aim<1 || aim>N || K < 1 || N < 2) {
		return -1;
	}
	return process(start, K, N, aim);
}

傻缓存法

分析递归的过程，以当前在7位置，剩余10步。

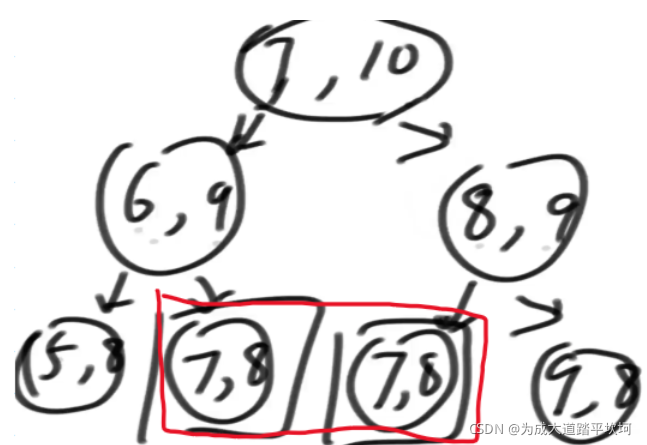
当前过程中存在重复的子问题，为了避免重复的计算，可以将已经计算过的递归过程，存放在一张表中，本题的可变参数有两个，所以可以用二维数组来表示这个表。

加缓存存放已经计算过的子问题，解决重复子问题，这种方法就是傻缓存法，从顶向下的动态规划也叫记忆化搜索。

寻找可变参数，cur当前位置 1-N，rest范围0-K

所以准备一个二维数组，将上面的两个参数随意组合后的返回值，装在dp数组中，先将数组初始化为-1，若为-1则说明没有计算过，若不是-1，直接返回对应的dp值。

int process1(int cur, int rest, int N, int aim, vector<vector<int>>& dp) {
	if (dp[cur][rest] != -1) {
		return dp[cur][rest];
	}
	int ans = 0;
	if (rest == 0) {
		ans = cur == aim ? 1 : 0;
	}
	else if (cur == 1) {
		ans = process1(2, rest - 1, N, aim, dp);
	}
	else if (cur == N) {
		ans = process1(N - 1, rest - 1, N, aim, dp);
	}
	else {
		ans = process1(cur - 1, rest - 1, N, aim, dp) + process1(cur + 1, rest - 1, N, aim, dp);
	}
	dp[cur][rest] = ans;
	return ans;
}
//傻缓存法
int way2(int N, int start, int aim, int K) {
	if (start<1 || start>N || aim<1 || aim>N || K < 1 || N < 2) {
		return -1;
	}
	vector<vector<int>>dp(N + 1, vector<int>(K + 1, 0));
	for (int i = 0; i <= N; i++) {
		for (int j = 0; j <= K; j++) {
			dp[i][j] = -1;
		}
	}
	return process1(start, K, N, aim, dp);
}

动态规划

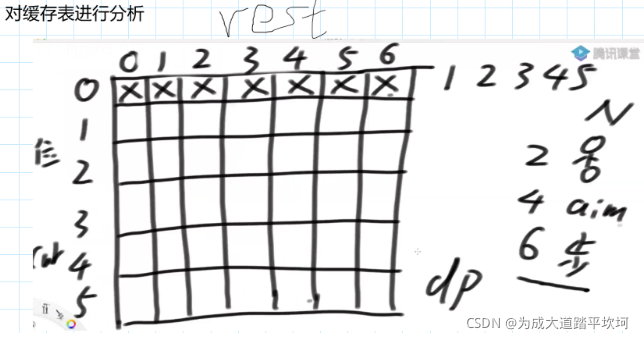
把dp表画出来，分析依赖关系。行增加方向为当前的位置，列增加方向为剩余步数，建一个N+1行，K+1列的dp表，由于当前的位置不能到达0，所以第一行用不着。先看我们要求的位置是哪个，根据之前主函数调用递归，得知最终求得位置是dp[2][6]

再看basecase：

当rest==0 的时候，也就是第一列，只有当cur当前位置在aim目标位置时，值为1，其他的值都是0。

再开始看递归过程中的位置依赖关系：

当cur==1的时候，也就是第一行，依赖的位置是2，rest-1，也就是该位置的左下角位置。

当cur==N的时候，也就是最后一行，依赖的位置是N-1，rest-1，也就是左上角的位置。

再来看普遍位置，依赖的是左上位置和左下位置，值为两者的和。

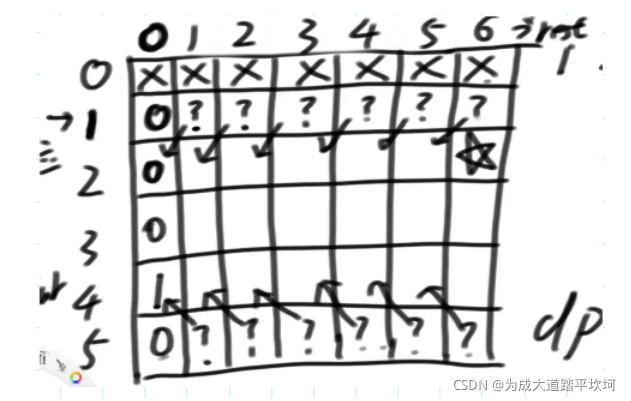
接下来就是用代码计算整个表的值，返回所要求的的位置的值即可。

int way3(int N, int start, int aim, int K) {
	if (start<1 || start>N || aim<1 || aim>N || K < 1 || N < 2) {
		return -1;
	}
	vector<vector<int>>dp(N + 1, vector<int>(K + 1, 0));
	dp[aim][0] = 1;
	for (int rest = 1; rest <= K ; rest++) {
		dp[1][rest] = dp[2][rest - 1];
		for (int cur = 2; cur < N; cur++) {
			dp[cur][rest] = dp[cur - 1][rest - 1] + dp[cur + 1][rest - 1];
		}
		dp[N][rest] = dp[N - 1][rest - 1];
	}
	return dp[start][K];
}

在填表的过程中，第一行的数字和最后一行的数字，都只依赖一个位置，所以可以做一下优化，将其直接取值赋值，不再需要麻烦的进行判断。

主函数

int main(int argc, char** argv) {
	cout << way1(5, 2, 4, 6)<<endl;
	cout << way2(5, 2, 4, 6) << endl;
	cout << way3(5, 2, 4, 6)<<endl;
	return 0;
}