新年第一篇,最近开始学习数据结构和算法的课程,课程的里给的代码是用java写的,
我打算自己听完课后整理一下内容,然后尽量用c++实现,起到一定的复习和巩固的作用。
01 时间复杂度
一个操作如果和样本的数据量没有关系,每次都是固定时间内完成的操作,叫做常数操作。
那常见的常数操作有哪些呢?
- 寻址操作,例如
int a=air[i]; - 加减乘除
- 位运算
时间复杂度是一个算法流程中,常数操作数量的一个指标,常用O表示。
具体来说,先要对一个算法流程非常熟悉,然后去写出这个算法流程中,发生了多少次常数操作,进而总结出常数操作数量的表达式。在表达式中,只要高阶项,不要低阶项,也不要高阶项的系数,剩下的部分如果为f(N),那么时间复杂度为O(f(N))。
评价一个算法流程的好坏,先看时间复杂度的指标,然后再分析不同数据样本下的实际运行时间,也就是常数项时间。
02 选择排序与冒泡排序
选择排序
选择排序就是在一个数组中,选择无序序列中的最左边的数,依次与序列中的数进行比较,如果这个数遇到了比它小的数,就将最小值指标指到当前位置,序列遍历一次以后,就把序列最左侧的值和当前指向的最小的值交换位置,使目前看到的最小值位于无序序列的最左侧,遍历完成一轮以后,最小的数到达序列的最左端,便从第二个数开始继续遍历交换,将剩下元素的最小值交换到第二个位置。
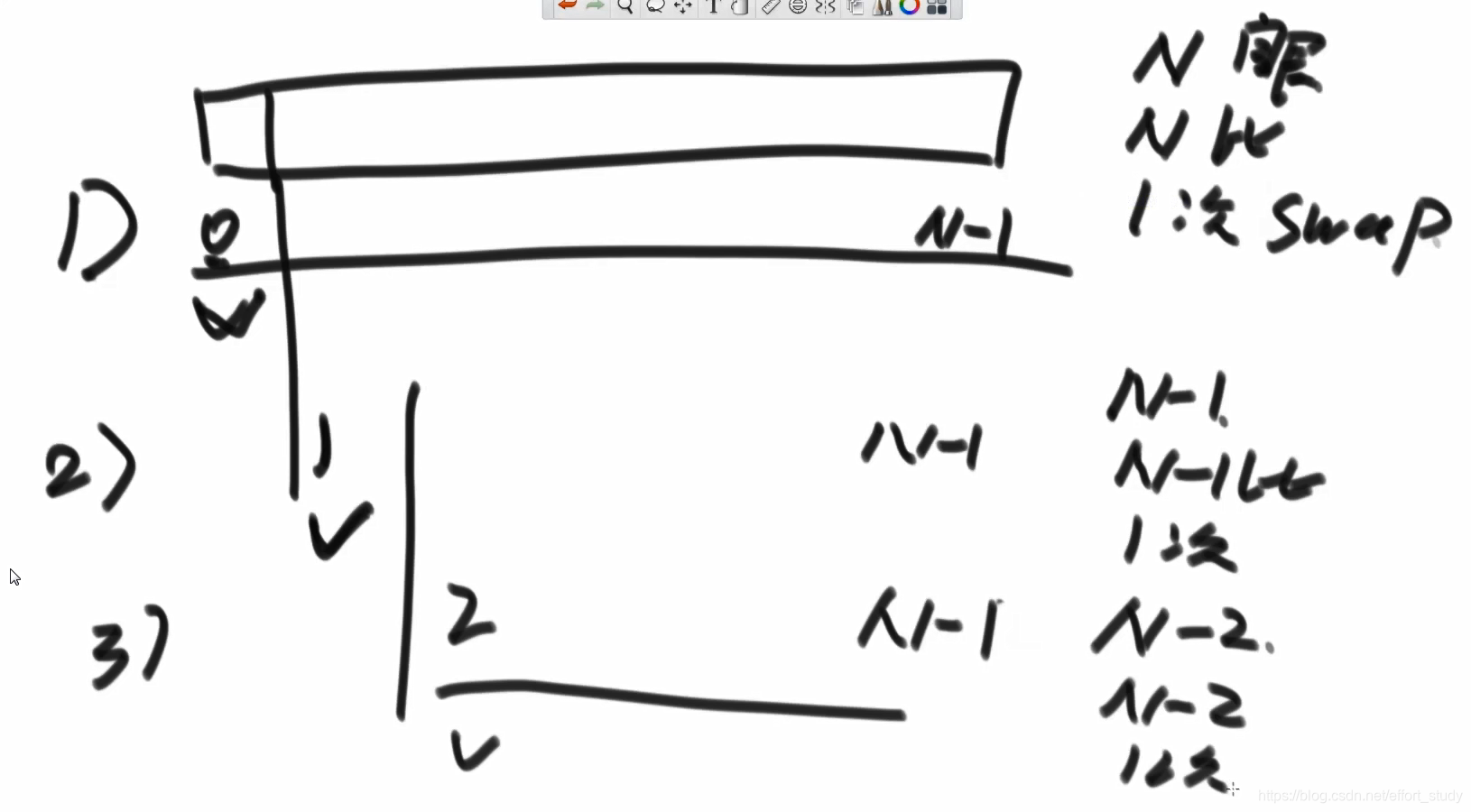
每次遍历需要看一眼当前的序列(寻址操作),然后再进行比较,最后再进行一次交换。将所有的次数加起来,按照O的计算方法,这个排序的时间复杂度是O(N^2)的。
代码实现
#include<iostream>
using namespace std;
void swap(int& a, int& b) {
//a = a + b;
//b = a - b;
//a = a - b;
int x = a;
a = b;
b = x;
}
void selectionSort(int *arr,int len) {
for (int i = 0; i < len-1; i++) {
int minIndex = i;
for (int j = i + 1; j < len; j++) {
minIndex = arr[j] < arr[minIndex] ? j : minIndex;
}
swap(arr[i], arr[minIndex]);
for (int i = 0; i < 10; i++) {
cout << arr[i] << " ";
}
cout << endl;
}
}
int main(){
int a[] = { 8,9,5,3,6,7,4,6,5,4 };
for (int i = 0; i < 10; i++) {
cout << a[i]<<" ";
}
cout << endl;
selectionSort(a, 10);
cout << endl;
for (int i = 0; i < 10; i++) {
cout << a[i] << " ";
}
int s = 7;
int b = 7;
swap(s, b);
cout << endl;
cout << s;
cout << b;
}
i的值记录的是当前无序序列第一个的位置,变化范围是0-长度减2(数组的址)本例中数组长度为10,则需要检查从第一个位置到第九个位置,按数组的址来说就是(0-8)。
程序中minIndex的值是当前无序序列中最小值的位置,从无序序列的第一个位置(也就是i位置)开始。
与第二个位置j比较,j会不断后移,遍历剩余的所有元素,若记录的minindex位置的值(当前最小值)大于j位置的值,则将minindex更新。
最后的交换操作,使用一个额外变量,进行交换。若是使用同一个变量交换,不用额外变量的方法交换后,值变为0。
冒泡排序
第一个for控制执行次数,第二个for用于遍历整个无序的过程。比较相邻两个元素,若前一个比后一个大,则较大的与小的交换位置,每一轮移动,当前序列中的最大值,到达序列最后的位置,下一次遍历则不需要包含这个位置。
void BubbleSort(int* arr, int len) {
for (int e = len - 1; e > 0; e--) {
for (int i = 0; i < e; i++) {
if (arr[i] > arr[i + 1]) {
swap(arr[i], arr[i + 1]);
}
}
}
}
03插入排序
插入排序,类似于打扑克牌摸牌的过程。首先第一个位置的元素是有序的,接下来看0-1序列的元素,若1位置的元素比左边位置的元素小,那么交换,这个元素再往左比较。
两种停止情况:1. 左边的数比当前的数小。2. 当前数到达边界处,左边没有其他数。
void insertSort(int* arr, int len) {
for (int i = 1; i < len; i++) {
for (int j = i - 1; j >= 0 && arr[j] > arr[j + 1]; j--) {
swap(arr[j], arr[j + 1]);
}
}
}
04 二分法详解
在一个有序数组中,找某个数是否存在
使用二分法查找元素,判断中间元素的值与查找值的大小关系,分为三种情况,直接找到;查找值小于中间元素值,则在前半截中查找,更新r的值为中间位置的前一个;查找值大于中间元素值,则在后半段中继续查找,更新l值为中间位置的后一个。
#include<iostream>
using namespace std;
bool exit(int* arr, int num) {
int l = 0;
int r = 9;
int mid = 0;
while (l < r) {
mid = l + ((r - l) >> 1);
if (arr[mid] == num) {
return true;
}
else if (arr[mid] > num) {
r = mid - 1;
}
else {
l = mid + 1;
}
}
return arr[l] == num;
}
int main(){
int a[] = { 1,2,3,4,6,7,8,88,888,888888 };
cout << exit(a,888 );
}
在一个有序数组中,找>=某个数最左侧的位置
int nearstIndex(int *arr,int len,int value){
int L=0;
int R=len-1;
int index=-1;
while(L<R){
int mid=L+((R-L)>>1);
if(arr[mid]==value){
index=mid;
R=mid-1;
}else{
L=mid+1;
}
}
return index;
}
局部最小值问题
int getLessIndex(int* arr,int len) {
if (len == 1 || arr[0] < arr[1]) {
return 0;
}
if (arr[len - 1] < arr[len - 2]) {
return len - 1;
}
int left = 1;
int right = len - 2;
int mid = 0;
while (left < right) {
mid = (left + right) / 2;
if (arr[mid] > arr[mid - 1]) {
right = mid - 1;
}
else if (arr[mid] > arr[mid + 1]) {
left = mid + 1;
}
else {
return mid;
}
}
return left;
}
05 异或运算
异或运算的性质
0^N == N N^N == 0
相同为0不同为1,位运算还可以理解为无进位相加
异或运算满足交换律和结合律
不用额外变量交换两个数
这样做的前提是两个变量在内存中是独立的区域
a=a^b;
b=a^b;
a=a^b;
一个数组中一种数出现奇数次,其他数均出现偶数次,如何找出
void printOddTimesNum1(int *arr,int len){
int eor=0;
for(inti=0;i<len;i++){
eor^=arr[i];
}
cout<<eor;
}
一个数组中两种数出现奇数次,其他数均出现偶数次,如何找出
void printOddTimesNum2(int *arr,int len){
int eor=0;
for(inti=0;i<len;i++){
eor^=arr[i];
}
int rightOne=eor&(~eor+1);
int onlyOne=0;
for(inti=0;i<len;i++){
if((arr[i]&rightOne)==1){
onlyOne^=arr[i];
}
}
cout<<onlyOne;
cout<<(eor^onlyOne);
}
06 对数器
1.有一个你要测的方法a;
2.实现一个绝对正确即使复杂度不好的方法b;
3.实现一个随机样本产生器;
4.实现比对的方法;
5.把方法a和方法b比对很多次来验证方法a是否正确
6.如果有一个样本使得比对出错,打印样本分析是哪个方法出错
7.当样本数量很多时比对测试依然正确,可以确定方法a已经正确
#include<iostream>
#include<vector>
#include<random>
#include<cassert>
#include<algorithm>
#include<ctime>
using namespace std;
default_random_engine e;
// 自己实现插入排序
void InsertSort(vector<int> &list) {
if (list.size() < 2) {
return;
}
for (int i = 1; i < list.size(); i++) {
for (int j = i - 1; j >= 0 && list[j + 1] < list[j]; j--) {
swap(list[j], list[j + 1]);
}
}
}
// for test
vector<int> generateRandomArray(int maxSize, int& size, int minValue, int maxValue) {
assert(minValue < maxValue);
size = e() % maxSize + 1;
vector<int> list(size);
for (int i = 0; i < list.size(); i++) {
list[i] = e() % (maxValue - minValue) + minValue;
}
return list;
}
// for test
vector<int> copyArray(vector<int> list, const int n) {
vector<int> list2(n);
list2.assign(list.begin(), list.end());
return list2;
}
// for test
void rightMethod(vector<int>& list, const int size) {
sort(list.begin(), list.end());
}
// for test
bool isEqual(vector<int>& list1, vector<int>& list2, const int size) {
for (int i = 0; i < size; i++) {
if (list1[i] != list2[i])
return false;
}
return true;
}
// for test
void printArray(vector<int>& list, const int size) {
for (int i = 0; i < size; i++) {
cout << list[i] << " ";
}
cout << endl;
}
void testAlgorithm() {
int testTime = 500000;
int maxSize = 10;
int minValue = -100;
int maxValue = 100;
bool succeed = true;
clock_t startTime, endTime;
int size = 0;
startTime = clock();
for (int i = 0; i < testTime; i++) {
vector<int> list = generateRandomArray(maxSize, size, minValue, maxValue);
vector<int> list1 = copyArray(list, size);
vector<int> list2 = copyArray(list, size);
InsertSort(list1);
rightMethod(list2, size);
if (!isEqual(list1, list2, size)) {
succeed = false;
printArray(list2, size);
break;
}
}
cout << (succeed ? "NICE" : "FUCKED") << endl;
endTime = clock();
cout << "time cost:" << (double)(endTime - startTime) / CLOCKS_PER_SEC << "s" << endl;
}
int main()
{
testAlgorithm();
system("PAUSE");
return 0;
}





 博客介绍了算法基础内容,包括时间复杂度的概念与计算方法,选择排序、冒泡排序、插入排序的原理及时间复杂度,二分法在有序数组中的查找应用,异或运算的性质及相关问题求解,还阐述了对数器的实现步骤,用于验证算法正确性。
博客介绍了算法基础内容,包括时间复杂度的概念与计算方法,选择排序、冒泡排序、插入排序的原理及时间复杂度,二分法在有序数组中的查找应用,异或运算的性质及相关问题求解,还阐述了对数器的实现步骤,用于验证算法正确性。
















 1563
1563

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








