层次化自监督单目深度估计

面向自动驾驶应用的层次化自监督单目绝对深度估计

摘要

近年来，用于单目深度估计的自监督方法已迅速成为深度估计任务的一个重要分支，尤其是在自动驾驶应用中。尽管整体精度较高，但现有方法仍存在以下问题：a）物体级深度推断不准确；b）尺度因子不确定。前者会导致纹理复制或物体边界不准确，后者则要求现有方法依赖额外传感器（如激光雷达）提供深度真实值，或使用双目相机作为附加训练输入，从而增加了实现难度。在本研究中，我们提出DNet来同时解决这两个问题。我们的贡献有两点：a）提出一种新颖的密集连接预测（DCP）层，以实现更优的物体级深度估计；b）针对自动驾驶场景，引入密集几何约束（DGC），使得自动驾驶汽车无需额外成本即可恢复精确的尺度因子。我们进行了大量实验，结果证明DCP层和DGC模块分别有效解决了上述问题。得益于DCP层，深度图中的物体边界得以更好地区分，且物体级别的深度更加连续。实验还表明，在给定相机高度且地面点占像素比例超过1.03%的情况下，使用DGC进行尺度恢复的性能可与使用真实值信息的方法相媲美。代码位于 https://github.com/TJ-IPLab/DNet。

引言

从单张RGB图像中估计精确深度图在3D场景理解以及增强现实和自动驾驶等许多实际应用中具有重要意义。与传统的手工特征方法[1],监督学习[2],[3],[4],[5],[6],[7]和立体自监督[8],[9],[10],[11]学习相比，已被证明能够在该任务上实现更好的性能。然而，这些方法要么需要大量高质量标注的真实值，而这类数据难以获取，要么需要复杂的立体标定。因此，单目自监督学习方法成为研究焦点。一些近期研究[12],[13],[14],[15]揭示了其在解决单目深度估计任务方面的巨大潜力。

尽管现有方法有望达到令人满意的性能，但它们存在两个缺点。其中之一是只能估计相对深度，而无法估计绝对深度。在评估时，尺度因子通过真实值（由激光雷达提供）与预测深度中值的比值[12],[13],[14],[15]，如图1所示。理论上，这是一个不错的解决方案。然而，在实际应用中，使用其他传感器获取真实值不仅增加了成本，还使系统更加复杂，导致复杂的联合标定过程和同步问题。

另一个问题是，由于当前方法的解码器在不同分辨率下分别预测深度，导致一些物体级别的细节被忽略。例如，物体边界可能变得模糊，并且物体表面纹理的深度可能与物体本身的深度预测结果不同。

本文提出了一种新的自监督单目深度估计流程DNet，该方法利用密集连接的层次化特征来获得更精确的物体级别深度推理，并采用密集几何约束消除对附加传感器或深度真实值的依赖以实现尺度恢复，从而更易于投入实际应用。

我们的贡献如下所列：
- 我们通过提出一种新的密集连接预测（DCP）层来改进之前的多尺度估计策略。该提出的DCP层利用层次化特征，使得能够基于多尺度预测特征进行物体级深度推断，从而优化物体边界，而非在不同尺度下分别预测深度并计算重建损失。
- 引入了一种新颖的密集几何约束（DGC）模块，用于实现高质量的尺度恢复，以应用于自动驾驶。基于相对深度估计，DGC模块能够完成逐像素地面分割，并从每个地面点估计相机高度。采用统计方法确定相机高度，从而能够鲁棒地抑制地面点提取中的离群值。通过比较给定的和估计的相机高度，可以确定尺度因子。

DNet在KITTI的Eigen分割上进行了广泛评估，结果不仅表明DCP层能够提升物体级别深度推理的性能，还证明了使用DGC模块的DNet在尺度因子确定方面与那些使用深度真实值的方法相比具有竞争力。消融实验验证了模块的有效性以及DNet对地面点比例的敏感性。

II. 相关工作

A. 自监督单目深度估计

单目深度估计一直是场景理解中的一个重要方面。一些研究采用监督学习[2],[3],[4],[5],[6],[7]或立体自监督[8],[9],[10],[11]方法来解决该问题。然而，由于获取大量标注数据或进行复杂的立体标定以训练深度估计网络存在困难，因此提出了单目自监督方法[12],[13],[14],[15]。

由开创性工作[15]提出，其基本思想是通过比较目标图像与从邻近源视图重建的目标视图来计算光度重建损失。然而，该方法假设场景是静态的，并且在不同连续帧之间不存在遮挡。[17],[18],[19]明确建立了不同的运动模型以解决动态场景问题。[20]通过构建两个附加层引入了三维表面法线，以实现更优的深度估计。[14]将原始的光度重建误差替换为逐像素最小重投影误差，从而部分解决了遮挡问题。同时，它还采用了上采样方法，并提出了对静态像素的自动掩码，分别避免了由低纹理和运动物体产生的无限深度“空洞”。

然而，上述所有工作仅预测相对深度，这意味着预测结果与真实深度之间仍存在尺度差距。为了评估目的，通常采用真实值与当前预测的中位数比率来获取绝对深度。遗憾的是，在实际应用场景中，深度真值要么难以获取，要么经济成本过高。因此，亟需一种无需深度真值的尺度恢复方法。

B. 单目尺度恢复

尺度不确定性一直是单目相机三维视觉的一个难题。为了恢复尺度因子并实现绝对深度估计中，[21]利用位姿信息，而[22]使用立体数据对网络进行预训练，两者均引入了额外传感器信息，但结果并不令人满意。除深度估计外，典型的例子是单目视觉SLAM。为了缓解这一问题，[23],[24]将目标检测算法集成到单目视觉SLAM系统中，并利用物体尺寸先验来恢复尺度。然而，除了计算复杂度显著增加外，这些方法在缺乏已知物体类别的场景下表现出的鲁棒性也较为有限。

处理相机与地面之间的几何关系也是解决该问题的有效方法。这种几何约束在自动驾驶任务中被广泛使用，因为车载相机拍摄的图像中通常包含地面。这些方法的主要任务是利用相机‐地面几何约束来估计相对相机高度，并结合绝对相机高度先验推断尺度。[25]使用训练好的分类器提取地面，但其泛化能力不足。[26]在感兴趣区域内密集地提取地面点，类似于[27],[28]，但需要引入稠密立体视觉系统，可能增加成本和复杂性。在[29]（与本文最相似的工作）中，利用表面法线提取地面点，进而计算相机高度。然而，由于其基于关键点的策略导致稀疏性，需通过连续帧进行数据关联，使得该方法难以集成到仅以单帧图像作为输入的单目深度估计任务中。此外，该方法将地面视为一个整体的、平坦的面板，具有单一的表面法线，这对于自动驾驶场景而言是一个较强的假设。相比之下，我们的方法无需数据关联，因此可同时集成到单目深度估计和视觉SLAM任务中。此外，我们的方法实现了逐像素表面法线计算和地面分割，使算法对自动驾驶中的不同道路条件具有更强的鲁棒性。

III. 方法

在本节中，提出了一种名为DNet的新型流程，专门用于自动驾驶应用中的单目绝对深度估计。该流程可分为两个部分：分别用于相对深度估计，并采用密集连接预测（DCP）层以提升物体级深度推断；以及基于密集几何约束的尺度恢复，无需任何额外传感器信号或深度真实值。DNet的整体结构如图2所示。

A. 相对深度估计

所提出的DNet基于Monodepth2[14]。与所有自监督深度估计方法一样，其在物体级别的推理上仍可能存在纹理复制和不精确的物体边界问题。在本节中，我们将首先介绍Monodepth2，然后通过引入DCP层替换Monodepth2中使用的全分辨率模块来解决此问题。

1) 基线：无全分辨率的Monodepth2

架构 ：在单目自监督架构中需要两个网络，分别为深度网络和位姿网络。将第t帧的单张图像It作为深度网络的输入。深度网络输出一个密集的相对深度图Drel_t。位姿网络依次将{It−1,It}和{It,It+1}作为输入，然后输出第t帧图像相对于第(t−1)帧和第(t+1)帧图像的相机位姿，即{Trel_t→t−1,Trel_t→t+1}。

自监督损失 ：总损失由两部分构成，分别为逐像素最小重构损失Lp和逆深度平滑损失Ls。重构损失的计算首先通过逆向扭曲源图像{It−1, It+1}以重建两个目标图像{It−1→t,It+1→t}。随后，结合结构相似性指数（SSIM）[30]以及两幅图像Ia,Ib之间的L1范数，计算重构图像与目标图像之间的光度误差（PE），公式如下：

$$
PE(I_a, I_b) = \alpha \frac{1 - SSIM(I_a, I_b)}{2} + (1-\alpha)|I_a - I_b|_1, \quad (1)
$$

其中α用于权重调整。

然后按如下方式计算每个像素的最小损失Lp：

$$
L_p = \min_{I’} (PE(I’, I_t)), \quad (2)
$$

其中I′ ∈ {It−1→t, It+1→t, It−1, It+1}。

结合边缘感知平滑损失Ls：

$$
L_s = |\partial_x d^ _t| e^{-|\partial_x I_t|} + |\partial_y d^ _t| e^{-|\partial_y I_t|}, \quad (3)
$$

其中$\bar{d^*_t} = d_t / \bar{d_t}$是均值归一化逆深度，总损失可以用两个超参数µ和λ构建为：

$$
L_i = \sum_i (\mu L_{p,i} + \lambda w_i L_{s,i}), \quad (4)
$$

其中，下标i表示解码器的不同分辨率层。wi根据分辨率确定。

2) DNet & 密集连接预测层

总损失 ：由于低分辨率深度预测的光度误差可能是由网络预测错误或下采样混叠引起的，对低分辨率和高分辨率结果在损失中使用相同的权重可能会误导网络收敛到非最优值。此外，考虑到低分辨率特征被多次重用，因此降低低分辨率深度预测误差的权重如下：

$$
L_i = \sum_i (\mu v_i L_{p,i} + \lambda w_i L_{s,i}). \quad (5)
$$

其中vi < 1被引入作为权重调整参数。

DCP层 ：为了处理由双线性采样引起的局部梯度[31]和局部极小值，当前研究[12],[13],[14],[15]包括我们的基线Monodepth2采用多尺度深度预测策略。该策略通过重复的上采样层隐式地利用低分辨率特征进行深度预测，容易产生深度伪影（图9）。为了减少深度伪影并获得更合理的物体级深度推断，我们提出了一种新的DCP层，能够层次化地显式融合不同尺度的特征。这一设计的直觉来源于观察到解码器网络的低分辨率层能提供更可靠的物体级深度推断，而高分辨率层则更关注局部深度细节。

形式上，DCP层中的卷积层将不同尺度的特征通道数减少至八个，从而使通道数量统一，并简化后续计算。低分辨率层中的特征随后被上采样并与高分辨率层特征拼接。通过这种方式，我们将更精确的物体级推理解释引入原本对物体级深度关注较少的高分辨率深度预测中。最终深度估计基于密集连接特征层提供的层次化特征进行。详细结构见图3。

B. 尺度恢复

在预测相对深度后进行尺度恢复，以便仅依靠单目图像生成绝对深度图。因此引入了密集几何约束(DGC)。DGC是专门为自动驾驶应用设计的，其工作假设是单目图像中存在足够的地面点，这在自动驾驶场景中通常是成立的。与基于特征的视觉里程计所采用的尺度恢复方法不同，DGC从单目图像中密集提取地面点，形成密集地面点图。如图5所示，地图中的每个点都用于估计一个相机高度。由此可以获得大量的相机高度。通过应用统计方法进行整体相机高度估计，离群值几乎不会对尺度因子的估计结果造成影响。

1) 表面法线计算

第一步是确定输入图像中每个像素的表面法线。所有像素点都需要根据以下方程投影到三维空间：

$$
D^{rel} t(p {i,j})p_{i,j} = KP_{i,j}, \quad (6)
$$

其中$p_{i,j} = [i, j, 1]^T$表示二维空间中具有一个齐次坐标的第i行第j列的像素，$P_{i,j} = [X, Y, Z]^T$是对应的三维点，$D^{rel} t(p {i,j})$是该特定点的深度，K是相机内参矩阵。

类似于[20]中的每个像素点，采用8邻域规则来确定其周围的若干平面，如图4所示。pi,j的全部8个邻域被分为4对。每对中的两个点分别与pi,j连接形成两个向量，这两个向量之间构成一个90度角，即$G(P_{i,j}) = {[P_{i+1,j}, P_{i,j-1}], [P_{i+1,j-1}, P_{i-1,j-1}]…}$。四对向量构成4个表面，从而生成4个表面法线，可通过以下公式计算：

$$
n_g = \overrightarrow{P_{i,j}G_{g,1}} \times \overrightarrow{P_{i,j}G_{g,2}}, \quad (7)
$$

其中Ga,b表示G中第a对元素的第b个元素(Pi,j)以及g=1,2,3,4。

点Pi,j的最终归一化表面法向量通过归一化并平均四个估计的法向量得到：

$$
N(P_{i,j}) = \frac{\sum_g n_g/|n_g|_2}{4}. \quad (8)
$$

2) 地面点检测

地面点通常指具有接近理想地面法向量的归一化法向量的点，即$\tilde{n}=(0,1,0)^T$。基于该理想目标法向量和计算得到的归一化表面法向量，我们提出一种基于余弦函数绝对值的相似性函数$s(P_{i,j})$。计算得到的相似性S可作为简单判据，用于判断Pi,j是否为地面点。

$$
S = s(P_{i,j}) = |\cos(\tilde{n}, N(P_{i,j}))| = \left|\arccos \frac{\tilde{n} \cdot P_{i,j}}{|\tilde{n}||P_{i,j}|}\right|, \quad (9)
$$

其中算子·表示内积运算。

考虑到估计表面法线以及相机坐标系的y轴与地面并非严格垂直（如图5所示）所带来的不确定性，设置了一个阈值$S_{max}$。对于$S < S_{max}$，该像素点被视为地面点。在所有像素点的地面点判断完成后，检测到一组地面点$GP={P_{i,j} | s(P_{i,j}) < S_{max}, y(P_{i,j}) > 0}$。

IV. 实验

本文提出了对DNet流程的全面实验评估。定量结果表明，我们提出的DNet在相对深度估计和尺度恢复方面均能实现具有竞争力的性能。此外，通过消融研究证明了所提出的DCP层的有效性。由于DGC尺度恢复模块依赖于足够的可见地面，因此在不同地面点比例下的实验展示了DGC尺度恢复模块的鲁棒性。

A. 实现细节

使用的训练参数和方法与Monodepth2相同。具体而言，我们设置 µ= 1, λ= 0.001，且SSIM的 α等于 0.85。训练期间仅使用单目图像序列。对于尺度恢复，角度阈值为Smax= 5。对低分辨率预测分配较低的值，即v= w={1/8, 1/4, 1/2, 1}。

实验在配备 Intel Xeon 8163 CPU (2.5GHz) 和 NVIDIA RTX 2080 Ti 的计算机上进行。

B. 评估数据集

所有用于评估DNet的实验均在包含697张测试图像的KITTI Eigen分割[2]上进行[16] 2015 。为了评估深度估计结果，该数据集包含了从激光雷达3D点云投影到2D深度图的真实值。然而，对于将相对深度图转换为绝对深度图所需的尺度因子，并没有提供真实值。通常采用的方法是使用激光雷达检测的深度值与估计深度值的中位数比率作为尺度因子的真实值。

C. 定量评估

全面的定量评估展示了DNet流程在相对深度估计上的整体性能以及绝对深度估计。采用常用指标进行评估。

表I
DNet Pipeline与现有方法的性能比较。现有方法的实验结果来自各自论文。对于尺度因子，GT是使用激光雷达深度真值，P是使用附加位姿信息，S是使用立体预训练网络，DGC是我们提出的密集几何约束方法。BOLD AND UNDERLINED DATA DENOTES THE BEST AND SECOND BEST PERFORMANCE RESPECTIVELY.

方法	尺度因子	绝对相对误差	平方相对误差	RMSE	对数均方根误差	δ< 1.25	δ< 1.25²	δ< 1.25³
Zhou 等人 [15] CVPR’17	GT	0.183	1.595	6.709	0.270	0.734	0.902	0.959
Yang 等人 [20] AAAI’18	GT	0.182	1.481	6.501	0.267	0.725	0.906	0.963
Mahjourian 等人 [32] CVPR’18	GT	0.163	1.240	6.220	0.250	0.762	0.916	0.968
LEGO [13] CVPR’18	GT	0.162	1.352	6.276	0.252	-	-	-
DDVO [33] CVPR’18	GT	0.151	1.257	5.583	0.228	0.810	0.936	0.974
DF-Net [34] ECCV’18	GT	0.150	1.124	5.507	0.223	0.806	0.933	0.973
GeoNet [18] CVPR’18	GT	0.149	1.060	5.567	0.226	0.796	0.935	0.975
EPC++ [17] TPAMI’18	GT	0.141	1.029	5.350	0.216	0.816	0.941	0.976
Struct2Depth [12] AAAI’19	GT	0.141	1.026	5.291	0.215	0.816	0.945	0.979
CC [35] CVPR’19	GT	0.139	1.032	5.199	0.213	0.827	0.943	0.977
Bian 等人 [36] NIPS’19	GT	0.128	1.047	5.234	0.208	0.846	0.947	0.976
Monodepth2 [14] ICCV’19	GT	0.115	0.903	4.863	0.193	0.877	0.959	0.981
DNet（我们的）	GT	0.113	0.864	4.812	0.191	0.877	0.960	0.981
Pinard 等人 [21] ECCV’18	P	0.271	4.495	7.312	0.345	0.678	0.856	0.924
Roussel 等人 [22] IROS’19	S	0.175	1.585	6.901	0.281	0.751	0.905	0.959
DNet（我们的）	DGC	0.118	0.925	4.918	0.199	0.862	0.953	0.979

越低越好 / 越高越好

表 I 展示了DNet在使用真实值（GT）和DGC尺度恢复情况下的整体深度估计性能，并与14种自监督单目深度估计器进行了比较。首先评估了使用真实值尺度恢复的DNet，以展示其相对深度估计性能。从表中可以看出，使用真实值尺度恢复的DNet取得了令人满意的结果。相较于Monodepth2，在前四项指标上分别提升了 1.74%、4.32%、1.05% 和 1.04%。

在绝对深度估计方面，DGC的表现几乎与真值尺度恢复相当。与Roussel等人[22]相比，DNet在前四项指标上分别实现了32.57%、41.64%、28.73% 和 29.18% 的改进。DGC模块的性能甚至超过大多数使用真值尺度恢复的早期深度估计器。这表明，尽管DGC尺度恢复方法较为简单，但仍能实现令人满意的尺度恢复效果。

D. 消融研究

为了更好地展示我们所提出模块的优势以及对地面点比例的鲁棒性，进行了全面的消融研究。

表II
ABLATION STUDY. 基线与我们提出的带有DCP层的DNet在性能上的比较。尺度因子由激光雷达地面真实值确定。

方法	绝对相对误差	平方相对误差	均方根误差	对数均方根误差	δ< 1.25	δ< 1.25²	δ< 1.25³
基线	0.117	0.894	4.899	0.195	0.871	0.958	0.981
Ours	0.113	0.864	4.812	0.191	0.877	0.960	0.981

越低越好 / 越高越好

表III
Ablation Study. 基线与我们采用提出的DCP层的DNet在物体级别预测性能上的比较。尺度因子由激光雷达真值确定。

方法	绝对相对误差	平方相对误差	均方根误差	对数均方根误差	δ< 1.25	δ< 1.25²	δ< 1.25³
基线	0.227	3.680	8.430	0.327	0.690	0.857	0.924
Ours	0.202	2.817	7.941	0.310	0.725	0.875	0.932

越低越好 / 越高越好

1) DCP层的优势 ：为了展示DCP层生成的层次化特征的有效性，将基线模型与DNet进行了比较，结果如表II所示。可以看出，我们提出的DCP层在前四项指标上的性能分别提升了3.42%、3.36%、1.78% 和 2.05%。

2) DCP层对物体级别预测的好处 ：由于不规则边界和纹理复制效应，物体上的深度估计可能具有挑战性。为了展示DCP层在物体级别预测上的改进，使用Mask-RCNN[37]生成测试文件中的物体掩码，如图6所示，并且仅在掩码区域内部计算误差指标。

区域。表 III 比较了基线模型与DNet在物体级别深度预测上的性能。我们提出的DCP层在前四项指标上分别提升了11.01%、23.45%、5.80%、2.14%的物体级别预测性能。

E. DGC尺度恢复对可见地面的鲁棒性

由于DGC尺度恢复在很大程度上依赖于地面点提取，因此应仔细评估其性能与单帧中地面点比例之间的关系。我们在Eigen分割的697张测试图像上进行评估，并绘制每帧的地面点比例和相应的尺度误差。结果如图7所示，其中x轴为地面点比例，y轴为 (DGC−GT)/GT。可以看出，当地面点比例大于1.03%时，所提出的DGC模块能够表现得与真值尺度恢复一致且鲁棒。但在极低的地面点比例情况下，尺度可能会被估计错误。

表IV
DNet的速度性能。

阶段	耗时
推理	50.0毫秒
DGC尺度恢复	4.1毫秒

F. 定性评估

定性结果在图8和图9中展示。图8展示了整体的绝对深度估计结果以及表面法线和地面点掩码等中间结果。图9直观地展示了引入DCP相较于基线所带来的改进。可以看出，物体边界更加精确，且深度伪影在一定程度上被消除。

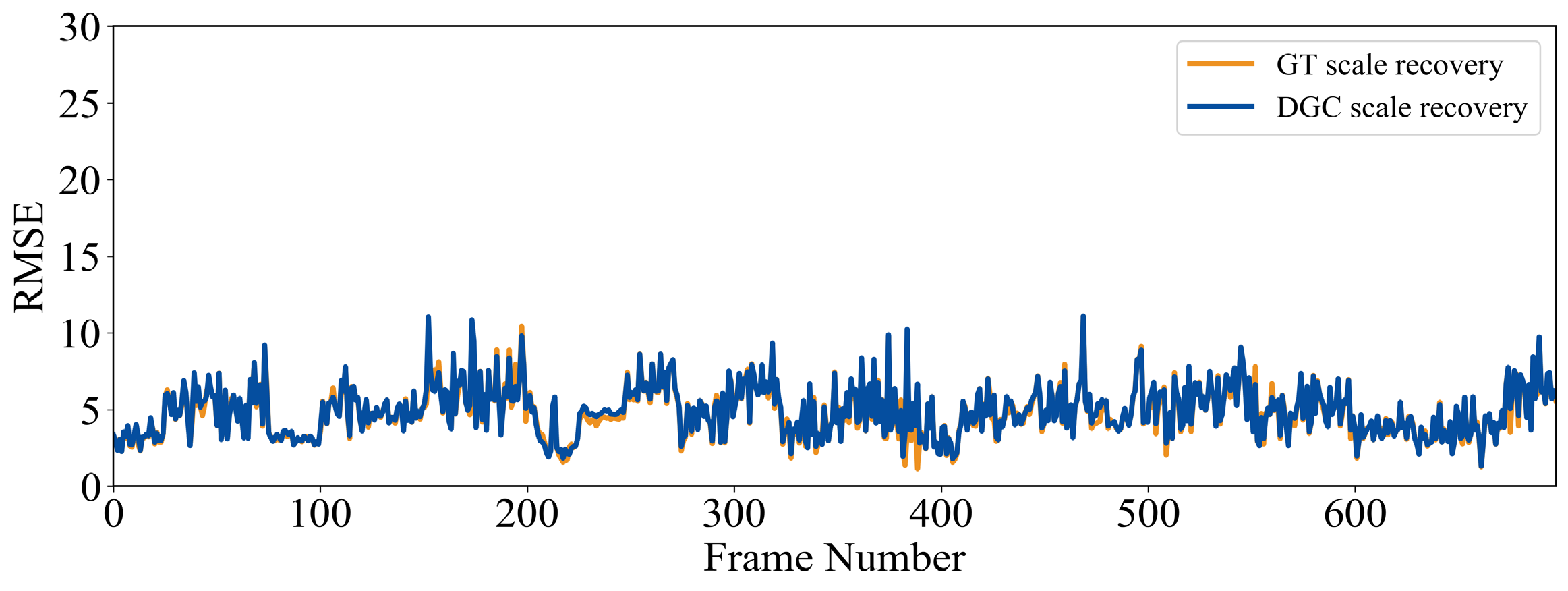
表V
QUANTITATIVE RESULT IN SCENES LISTED IN FIG. 10。当地面点比例相对较高时，DGC通常在至少一个指标上优于GT尺度恢复。

帧	尺度因子	绝对相对误差	平方相对	均方根误差	对数均方根误差
#106	GT	0.195	1.443	6.416	0.320
#106	DGC	0.110	1.105	5.799	0.319
#183	GT	0.194	1.175	5.888	0.231
#183	DGC	0.127	0.995	5.745	0.229
#330	GT	0.211	1.100	4.138	0.270
#330	DGC	0.144	0.844	4.174	0.271
#395	GT	0.353	2.181	5.837	0.418
#395	DGC	0.273	1.754	5.834	0.470

越低越好

G. DGC与地面实况的额外对比

还有结果表明，在某些情况下，DGC尺度恢复的效果甚至优于真值尺度恢复，尤其是在地面点比例相对较大的那些场景中。这些场景的一些示例如图10所示。这些帧中的性能表现见表V。令人惊讶的是，在至少31.7%且最多45.2%的帧中，DGC尺度恢复模块在四项指标上的表现更优。DGC相对于真值尺度恢复表现更优的帧比例的详细结果见表VI。

表VI
RATIO OF THE FRAMES WHERE DGC SCALE恢复在不同指标方面优于GT的帧所占比例。可以看出，尤其在绝对相对误差方面，DGC在许多帧中表现更优。

评估指标	比例
绝对相对误差	45.2%
平方相对误差	38.5%
RMSE	39.3%
对数均方根误差	31.7%

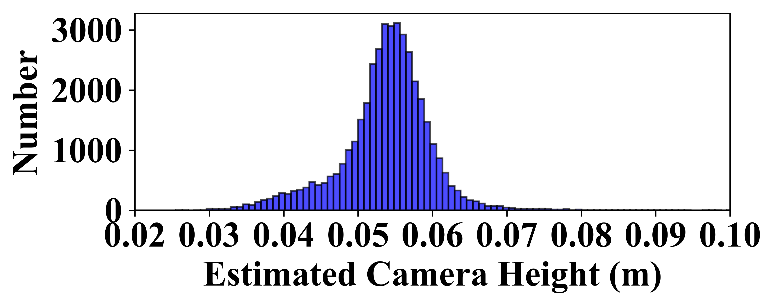
V. 结论

本文提出了一种用于自监督单目绝对深度估计的新型流程。提出了DCP层以生成用于高分辨率深度推理的层次化特征，从而使物体边界能够更准确的深度预测并更好地解决深度伪影问题。为了使自监督单目深度估计更易于适应和应用于自动驾驶应用，引入了DGC模块以在无需附加传感器和深度真值的情况下实现绝对深度预测。进行了大量实验，以验证所提出的DNet流程以及DCP和DGC模块的有效性和鲁棒性。

未来，这项工作为更好地利用层次化特征提供了直观启示，并可作为进一步探索尺度恢复方法的基础。